2. Applications

Manipuler, créer et utiliser des fonctions (exercice_A31.py)

Résolution d'une équation du second degré

Définir une fonction qui permet de calculer la ( ou les ) solution(s) d'une équation du second degré du type a.x² + b.x + c = 0

• la fonction aura comme paramètres les 3 coefficients a,b et c de l'équation.
• elle devra retourner la ( ou les ) solution(s) de l'équation, ou indiquer si il n'y en a pas !

Réfléchissez bien aux pré- et post-conditions de votre fonction, et complétez sa docstring. Testez ensuite le bon fonctionnement de votre fonction en réalisant plusieurs tests.

On va tester votre fonction sur un cas connu pour voir une limite de l'utilisation d'un ordinateur pour résoudre des équations faisant intervenir des nombres réels : ${(x+\sqrt{3})}^2=x^2+2\sqrt{3}x+3=0$ admet une racine double $x=-\sqrt{3}$ donc on est dans le cas où $\Delta =0$ . Pour disposer de la fonction racine carrée (square root en anglais),

from math import sqrt

D'après votre fonction, combien de solution devrait-elle avoir ? Cette différence provient du fait que certais nombres réels (comme $\sqrt{3}$ ici) ont besoin d'une infinité de chiffres pour les représenter correctement, or les capacités d'un ordinateur sont limités et il y a une approximation entre la vraie valeur de $\sqrt{3}$ et la valeur effectivement utilisée par python. Nous verrons cela plus en détails dans la partie B3.

Représentation de fonctions mathématiques

Travail n°1 : construction de la fonction

Définir, puis tester les fonctions suivantes :

1. Écrire une fonction f1() qui prend en paramètre une variable x et qui retourne la valeur du polynôme 2.x² - x + 3
2. Écrire une fonction f2() qui prend comme paramètre une liste L de valeurs, et qui retourne une nouvelle liste dont les éléments sont les images des éléments de L par la fonction mathématique 2.x² - x + 3
3. Écrire enfin une fonction f3() qui prend comme paramètres :
   • une chaîne de caractères contenant l'expression d'une fonction mathématique quelconque en syntaxe Python ( par exemple : x**2 + 2*x, 1/(2*x+3),....)
   • une liste L de valeurs
   et qui retourne une nouvelle liste dont les éléments sont les images des éléments de L par la fonction mathématique définie par la chaîne de caractères.

Pour la dernière fonction :

• il existe une fonction Python qui permet d'évaluer une expression, c'est à dire obtenir le résultat du calcul d'une expression, qu'on lui passe comme argument sous forme de chaîne de caractères.
  Il s'agit de la fonction eval(); voici comment elle s'utilise :

  
  x = 5
  y = eval("2*x**2 - x + 3") # l'argument doit être une chaîne de caractères ( ou une variable de type str )
  
  print(y)
  			

  
  48
  
  >>>
  			

  Pratique, non ? Attention cependant à respecter la syntaxe Python pour l'écriture des expressions...
• penser à faire des tests avec des listes courtes, et des expressions simples...

Travail n°2 : représentation graphique de la fonction

Vous allez utiliser le module Matplotlib pour tracer la représentation graphique d'une fonction mathématique quelconque.

Le module a besoin de deux listes pour tracer la représentation d'une fonction f : l'une dont les éléments sont les valeurs des abscisses x, et la deuxième dont les éléments sont les ordonnées y = f(x). Bien entendu, ces deux listes doivent avoir exactement le même nombre d'éléments.

Le module s’utilise ensuite très simplement; voila un exemple :

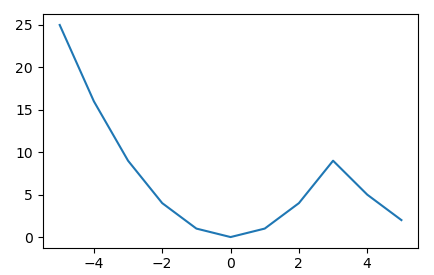
import matplotlib.pyplot as plt      # importation du module

x = [-5,-4,-3,-2,-1,0,1,2,3,4,5]    # liste pour les abscisses
y = [25,16,9,4,1,0,1,4,9,5,2]       # liste pour les ordonnées

plt.plot(x,y)  # tracé

plt.show()  # affichage
				

De nombreux paramétrages sont possibles; vous trouverez ici un mémento succinct.

Utiliser le module Matplotlib et la fonction f3() que vous avez écrit précédemment dans un script, qui demande à l'utilisateur d'entrer l'expression d'une fonction mathématique en syntaxe Python, et qui en trace la représentation graphique; à vous de réfléchir à la liste qu'il faudra passer en argument à la fonction.

Dessiner avec python (exercice_A32.py)

Le module Turtle de Python permet de dessiner en faisant se déplacer dans une fenêtre une "tortue" munie d'un "stylo"; on peut abaisser ou remonter le stylo, changer de couleur, faire avancer ou reculer la tortue, la faire tourner à gauche ou à droite,etc...

Vous pouvez découvrir ici les fonctions principales fournies par le module Turtle.

Le module s'importe en début de script avec l'instruction :

from turtle import *
		

Par défaut, la tortue ne fait que tracer des lignes; vous allez enrichir ses possibilités en écrivant quelques fonctions et procédures bien définies, de façon à pouvoir dessiner des figures plus sophistiquées.

Procédure carré

Voila un exemple de procédure qui permet de tracer un carré :

def carre():
	"""
	Procédure pour tracer un carré de côté 50px
	"""

	down()

	for i in range(4):
		right(90)
		forward(50)

	up()
		

1. utiliser cette procédure dans un script pour analyser son fonctionnement
2. modifier cette procédure de façon à pouvoir tracer un carré de longueur de côté quelconque passée en argument à la procédure
3. modifier enfin cette procédure de façon à pouvoir tracer un carré de longueur de côté quelconque, et pivoté d'un angle quelconque par rapport à l'horizontale. Attention, en fin de procédure, il faudra "compenser" cet angle dont la tortue aura tourné, de façon à ce qu'elle revienne dans la direction où elle allait avant l'appel de la fonction.

   Ne pas oublier de compléter la docstring de votre procédure !

4. Utiliser la fonction que vous venez de définir pour réaliser les figures suivantes :

Procédure étoile

Voila une procédure qui dessine un triangle équilatéral :