La fiche de cours est ici.
On cherche à déterminer si une valeur donnée N se trouve ou pas dans un tableau L .
Voila un travail que vous avez déjà fait il n'y a pas si longtemps, cette première partie devrait donc aller assez vite...
recherche_sequentielle qui :
Voila un petit jeu pour commencer : le nombre à deviner.
Un nombre aléatoire compris entre 1 et 100 est généré aléatoirement.
Vous devez le retrouver en moins de 10 essais.
Cet algorithme, ainsi que le précédent ( recherche séquentielle ) font partie de la liste des algorithmes à connaître pour l'épreuve pratique du BAC.
On va donc se servir, pour rechercher la présence d'une valeur dans un tableau, du fait que si celui-ci a été préalablement trié, on va pouvoir utiliser une méthode de recherche beaucoup plus efficace, la recherche par dichotomie. Dichotomie veut dire littéralement "couper en deux".
L'idée est de couper le tableau en 2 parties; on se retrouve avec 2 sous-tableaux de taille identique ( à un élément près dans le cas où le nombre total d'éléments du tableau est impair,
mais ça ne change rien ).
On garde uniquement le sous-tableau qui peut contenir la valeur recherchée : comme les sous-tableaux sont aussi triés, ce n'est pas difficile à déterminer, il suffit de
comparer la valeur recherchée avec l'élément délimitant les deux sous-tableaux, c'est à dire l'élément au milieu du tableau.
On recommence le processus jusqu'au moment où l'on se retrouve avec un tableau contenant un seul élément : si l'élément unique de ce tableau n'est pas l'élément recherché,
l'algorithme renvoie FAUX, et VRAI sinon ( et éventuellement, l'indice dans le tableau de la valeur recherchée ).
Valeur à rechercher :
Nombre d'étapes :
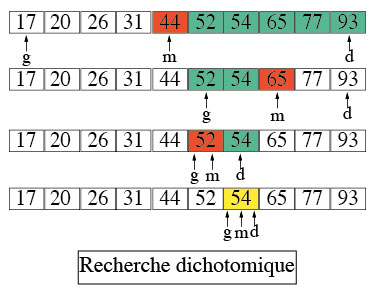
Voici l'algorithme de la recherche dichotomique; la précondition est que le tableau est trié :
tant que le tableau n'est pas réduit à un seul ou deux élément(s) :
si la valeur est égale à l'élément au milieu du tableau :
alors on a trouvé la valeur, on renvoie VRAI et l'indice de la valeur
sinon :
si la valeur est PLUS PETITE que l'élément au milieu :
alors elle se trouve forcément dans la partie GAUCHE du tableau : on recommence la recherche dans la partie GAUCHE du tableau
sinon si la valeur est PLUS GRANDE que l'élément au milieu :
alors elle se trouve forcément dans la partie DROITE du tableau : on recommence la recherche dans la partie DROITE du tableau
on a réduit le tableau à un seul élément, et on n'a pas trouvé la valeur : on renvoie donc FAUX
Avant de se lancer dans le code, il faut bien comprendre comme nous allons pouvoir coder ce qui apparaît dans l'algorithme dans les expressions "la partie GAUCHE du tableau" et "la partie DROITE
du tableau".
Pour cela nous allons utiliser des variables g, m, d, désignant les extrémités gauche et droite du tableau courant et m son milieu.
Les trois variables g ( = gauche ), m ( = milieu ) et d ( = droite ) servent à "délimiter" les deux sous-tableaux :
Dans l'image ci-dessous vous pourrez comprendre l'évolution des valeurs des variables g, m et d pour la recherche du nombre 16 dans le tableau fourni.

Coder en Python la fonction recherche_dicho réalisant la recherche dichotomique d'une valeur n dans un tableau tab trié.
Cette fonction renvoie l'indice de la valeur dans le tableau si elle s'y trouve, et -1 dans le cas contraire.
On a déjà parlé de complexité d'un algorithme quand on a travaillé sur la recherche "naïve" dans un tableau non trié ( Rappel : c'est O(n) ).
Nous allons essayer de trouver la complexité de l'algorithme par dichotomie
Il faut donc trouver le nombre d'étape nécessaires pour trouver un élément par dichotomie dans le pire des cas.
Ce que l'on cherche ici c'est le nombre d'étapes maximum pour gagner au jeu "deviner un nombre" en jouant "par dichotomie" (si on commence à jouer au hasard ).
Mais on cherche une relation générale pour une partie de jeu avec un nombre compris entre 1 et n...
La technique est donc de compter combien de fois il faut diviser par 2
le nombre n pour arriver à 1.
C'est assez simple quand on travaille avec des puissances de deux :
Bon ça commence à être un peu long tout ces tâtonnements !
Heureusement il existe une fonction mathématique qui fait ce calcul à notre place : c'est le logarithme de base deux.
Pour le trouver sur votre calculatrice Numworks, c'est très simple :

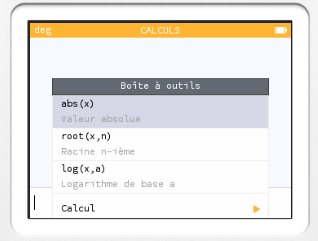
Appuyez sur la touche toolbox puis choisissez la troisième possibilité dans le menu ( pour les autres calculatrices appelez le professeur ).
Si vous n'avez pas votre calculatrice sous la main vous pouvez aller ici :https://www.numworks.com/fr/simulateur/.
Nous dirons alors que :
La complexité de la recherche dichotomique dans un tableau trié de n éléments est en O(log2(n)).
Vous pouvez simplement retenir que le logarithme en base 2 de n est le nombre de fois qu'il faut diviser n par 2 pour obtenir 1.
Conséquence : quand le nombre de données double, l'algorithme ne nécessite qu'une seule étape de plus; quand il est quadruplé, 2 étapes de plus, etc...
Cette notion est très importante, nous la retrouverons lors du tri de liste ou de l'étude des arbres binaires en terminale.
Et cette complexité est bien meilleure que celle de l'algorithme naïf, comme vous pouvez le voir ci-dessous :
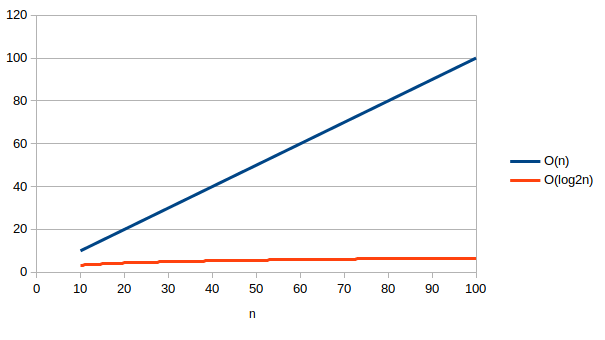
Comme toujours quand on parle de complexité, la différence entre les deux algorithmes apparaît pour de grandes valeurs de n.
Aujourd’hui nous faisons partie de l'équipe de codeurs du ministère des finances qui lutte contre l'évasion fiscale.
Notre objectif :
Être capables de retrouver rapidement des numéros de compte ou des sommes précises dans des listings dont le volume peut quelquefois dépasser le Teraoctet !.

tests_recherche.py contenant des fonctions qui vous permettront de mener à bien votre recherche.
timeit dont vous pourrez trouver un exemple d'utilisation ici.