Favicon

NSI Vaugelas - Première

Connexion

Sommaire

Algorithmes gloutons

Nous allons étudier une grande "famille" d'algorithmes : Les algorithmes gloutons (ou "greedy algorithm" en anglais).
Mais avant de définir les grandes lignes caractérisant cette classe, nous allons nous intéresser à un exemple classique, de la vie courante, où vous utilisez un algorithme glouton sans le savoir...

Un exemple : Le rendu de monnaie

Présentation du problème

Le rendu de monnaie est un problème du quotidien :
vous devez rendre 4,24€ avec un système de pièces et de billets donnés, en minimisant le nombre de pièce ou billets rendus.

rendu de monnaie

Vous avez déjà résolu ce problème de nombreuses fois, en suivant un algorithme "instinctif".
Nous allons essayer d'analyser votre résolution de ce problème et tenter de généraliser votre démarche à n'importe quelle somme et à n'importe quel système de monnaie (ensemble de pièces et de billets existants).

Le problème du rendu de monnaie c'est :

Quelques exemples

Pour bien comprendre la démarche à suivre nous allons commencer par rendre quelques sommes "à la main".

Nous allons considérer notre système de monnaie européen (sans les centimes): monnaie = [1, 2, 5, 10, 20, 50, 100, 200, 500].

1. Trouver TOUTES les possibilités pour rendre 7€ ( il y en a 6 différentes ) : - - - - - - 2. Parmi toutes ces possibilités, déterminer la solution OPTIMALE pour rendre 7€ :

SOLUTION

Cet exemple est "trivial", nous allons donc nous intéresser à un exemple plus difficile...

1. Nous allons tenter de rendre 263 €; d'après vous, comment trouver la la solution optimale de ce rendu ? 2. Faites le même raisonnement pour 264 €.

SOLUTION

Une fois que vous avez traiter ces deux exemples, nous allons nous orienter vers la formalisation de l'algorithme que vous utilisez instinctivement. Pour cela répondez aux questions suivantes :

1. Quel est le premier billet à rendre dans les deux cas précédents ? 2. Quels sont les deux critères pour choisir ce premier billet ? 3. Que faut-il faire une fois le premier billet rendu ? 4. Quel est le critère qui permet de savoir quand le rendu est complet ( = terminé ) ? 3. Écrire alors un algorithme qui traduit les opérations à faire pour rendre une somme quelconque à partir d'un ensemble 'monnaie' de pièces et de billets :

SOLUTION

Implémentation Python

Si vous avez répondu correctement aux questions précédentes, vous avez réussi à cerner l'algorithme que vous appliquez naturellement pour rendre la monnaie. Vous allez maintenant programmer cet algorithme.

Écrire une fonction rendu_glouton répondant aux spécifications suivantes :

Tester votre fonction sur les appels proposés, que vous avez étudiés ci-dessus ( et dont vous connaissez donc la solution ! )

def rendu_glouton(monnaie, somme): """ Fonction qui applique l'algorithme glouton de rendu de monnaie. Entrées : monnaie = le tableau des différents pièces et billets possibles, triés par valeur décroissante (list) somme = la valeur de la somme à rendre (int) Sortie : le tableau de pièces et billets à rendre (list) """ pass systeme = [100, 50, 20, 10, 5, 2, 1]

SOLUTION

rendu de monnaie

Les grands principes des algorithmes gloutons

un glouton ou 'gulo gulo'

Si votre fonction fonctionne correctement, vous avez réussi à programmer votre premier algorithme glouton; mais quelles sont les grands principes de cette classe d'algorithmes ?

Un algorithme glouton est un algorithme qui fait, à chaque étape de son exécution, un choix local optimal, sans retour en arrière ni anticipation des étapes suivantes, en "espérant" que cela conduise à une solution globale optimale.

Les algorithmes de cette classe n'étudient donc pas systématiquement toutes les solutions possibles afin d'en déduire la meilleure ( algorithmes dits de "force brute"), mais ils sont beaucoup plus rapides.

Dans l'exemple précédent, nous avions à chaque étape :

Et dans notre cas, CA MARCHE !!!.

Mais...les algorithmes gloutons ne "fonctionnent" pas toujours :

1. Rendez 6€ avec le système suivant : [4,3,1], en suivant votre algorithme. Est-ce optimal ? Justifier. 2. Rendez 8€ avec le système suivant [10,5,2]; mêmes questions ?

SOLUTION

Pour information, notre système de monnaie européen a été mis au point pour que l'algorithme de rendu de monnaie glouton soit toujours optimal !

Le problème du sac à dos

Présentation du problème

Le problème du sac à dos est un problème d'optimisation classique de l'informatique que nous allons tenter de résoudre grâce aux algorithmes gloutons.

Nous allons imaginer un voleur en train de dévaliser un appartement.

  • Il ne peut pas porter un sac de plus de 30 kg,
  • il veut ramener un butin maximum,

et il a devant lui plusieurs objets :

  • objet 1 : poids 13 kg et valeur 700 €
  • objet 2 : poids 12 kg et valeur 400 €
  • objet 3 : poids 8 kg et valeur 300 €
  • objet 4 : poids 10 kg et valeur 300 €

Il doit donc optimiser le remplissage de son sac.

© Boulet

Un peu de force brute (à la main !)

La technique de "force brute" consiste à attaquer un problème frontalement et à explorer toutes les possibilités en profitant de la force de calcul d'un ordinateur.
C'est une technique qui peut, par exemple, être utilisée pour trouver un mot de passe inconnu, en testant toutes les possibilités.

En considérant la liste d'objets ci-dessus, répondre aux questions suivantes:

1. Lister les chargements possibles du sac à dos sans se soucier du prix ou de la masse totale pour : 4 objets (1 solution c'est facile !) : - 3 objets (4 solutions) : - - - - 2 objets (6 solutions) : - - - - - - 1 objet (4 solutions c'est facile !) : - - - - 2. En vous mettant par groupe de deux, calculer ( et noter ci-dessus ) pour chaque chargement : - la masse (en kg) du chargement, - Le gain (en €) du chargement. 3. Éliminez les sacs de plus de 30 kg. 4. Déterminez les chargements optimaux :

SOLUTION

On peut remarquer qu'avec 4 objets, le problème est déjà assez complexe !
Mais dès que l'on dépasse 40 objets, un ordinateur actuel est incapable de le résoudre raisonnablement de cette façon !
En effet la complexité de ce problème en en O(2n), où n est le nombre d'objets.

1. Calculer 2**40 = 2. Si une opération sur l'ordinateur prend 1 ms = 10**-3 s, combien de temps ( en années ) prendront 2**40 opérations ?

SOLUTION

Et l'algorithme glouton ?

Comme on vient de le voir, il n'est pas envisageable de tester tous les cas, surtout si le nombre d'objets dépasse 30 ou 40.
Nous allons donc tenter d'appliquer la technique de l'algorithme glouton à ce problème.
Mais comment faire ?
Faut-il choisir initialement le plus petit objet, ou celui qui rapporte le plus ?

Et bien il faut OPTIMISER.
Nous allons donc calculer pour chaque objet sa "valeur massique" c'est à dire ce que rapportera un kg de cet objet :

  • objet 1 : poids 13 kg et valeur 700 €, valeur massique : 700/13 = 53,8 €/kg
  • objet 2 : poids 12 kg et valeur 400 €, valeur massique : 400/12 = 33,3 €/kg
  • etc...
  • on trie alors cette liste d'objets et on commence par celui qui rapporte le plus "au kg";
  • on vérifie que le sac n'est pas trop lourd si on l'ajoute, sinon on passe au suivant,
  • on enlève l'objet sélectionné de la liste des objets,
  • ...et on recommence avec les objets suivants !

Structure de données utilisée

Pour résoudre ce problème il faut d'abord penser à la structure de données qui pourra contenir la liste d'objets.
Sachant que chaque objet a 4 caractéristiques :

Il va donc être judicieux d'utiliser pour caractériser chaque objet un dictionnaire {nom, masse, valeur, gain_massique}; l'ensemble de ces dictionnaires sera alors stocké dans un tableau liste_objets :


liste_objets = [
    {"nom": "objet1", "masse": 13, "valeur": 700, "val_mas": None}, # pour l'instant, la valeur massique n'a pas encore été calculée
    {"nom": "objet2", "masse": 12, "valeur": 400, "val_mas": None},
    {"nom": "objet3", "masse": 8, "valeur": 300, "val_mas": None},
    {"nom": "objet4", "masse": 10, "valeur": 300, "val_mas": None}
    ]

Écrire une fonction calcule_gain, qui prend comme paramètre la liste des objets, et qui renvoie cette liste complétée avec la valeur massique calculée de chaque objet.

def calcule_gain(L): """ Complète une liste d'objets avec la valeur massique de chacun des objets de la liste. Entrée : la liste des objets sous la forme d'un tableau de dictionnaires [{nom, masse, valeur, None}] ( list de dict) Sortie : la liste complétée avec la valeur massique calculées de chaque objet : [{nom, masse, valeur, valeur_massique}] (list de dict) """ pass liste_objets = [ {"nom": "objet1", "masse": 13, "valeur": 700, "val_mas": None}, {"nom": "objet2", "masse": 12, "valeur": 400, "val_mas": None}, {"nom": "objet3", "masse": 8, "valeur": 300, "val_mas": None}, {"nom": "objet4", "masse": 10, "valeur": 300, "val_mas": None} ]

SOLUTION

Tri de la liste d'objets

Nous allons ici utiliser la fonction sort de Python, que vous avez déjà utilisée pour trier des tables de données.

  1. Écrire une fonction cle_tri, qui sera utilisée comme critère de tri pour le tableau liste_objets.
  2. utiliser cette fonction avec la fonction Python sort pour trier la liste des objets par valeur massique décroissante.
    3. def cle_tri(objet): pass

    SOLUTION

La fonction sac_a_dos

Voici ci-dessous un code incomplet, complétez le et testez le sur la liste d'objets données en introduction :

def sac_a_dos(Lobjets, msac): """ Fonction qui implémente l'algorithme de résolution du problème du sac à dos. Entrée : Lobjets = liste des objets triés par valeur massique décroissante (list de dict) msac = masse maximale du sac (int) Sortie: la liste des objets à sélectionner, la somme totale de ces objets, et la masse totale du sac. """ masse = 0 # masse totale somme = 0 # somme totale selection = [] # liste des objets à sélectionner for objet in Lobjets: pass

SOLUTION

Test de la fonction avec une liste d'objets plus conséquente...

C'est bien gentil, une liste de 4 objets...mais on aimerait savoir si l'algorithme résoudrait aussi, le problème avec une liste de 40 objets par exemple sans y passer la vie entière !

La fonction ci-dessous renvoie une liste aléatoire de n objets; utiliser cette fonction pour tester la robustesse de votre fonction sac_a_dos :

Ne pas donner une valeur trop grande à n...

from random import randint def creer_Lobjets(n): liste = [] for i in range(1, n+1): objet = {"nom": f"objet{i}", "masse": randint(1, 30), "valeur": randint(10, 100), "val_mas": None} liste.append(objet) return liste

Analyse de l'efficacité de l'algorithme glouton

Mais au fait, est-ce que notre algorithme glouton nous propose toujours "LA" solution optimale ?
Dans le cas de la liste liste_objets que vous avez utilisé pendant cette partie, cela semble être le cas.

On considère deux objets, l'un de 1 kg et l'autre de 30 kg.

Attribuez à chacun des objets une valeur qui fera que notre algorithme glouton ne sera pas optimal : - objet 1 : masse = 1 kg valeur = ... valeur massique = ... - objet 2 : masse = 30 kg valeur = ... valeur massique = ...

SOLUTION

Comme on l'a déjà dit, la "force brute" ne permet pas de trouver une solution quand il y a trop d'objets.
L'algorithme glouton lui proposera toujours rapidement une solution; elle ne sera "pas trop mauvaise" mais ne sera pas toujours optimale...

Il existe des solutions algorithmiques optimales à ces problèmes, qui peuvent faire appel, par exemple à la programmation dynamique vue en classe Terminale.

Application : un planning de films...

C'est la fête du cinéma ! Les salles de votre ville ont programmé une série de films qui seront projetés pendant 8h d'affilée.

Une quinzaine de films sont à l'affiche, qui n'ont pas la même heure de projection, ni la même durée; voila le planning prévu de projection :

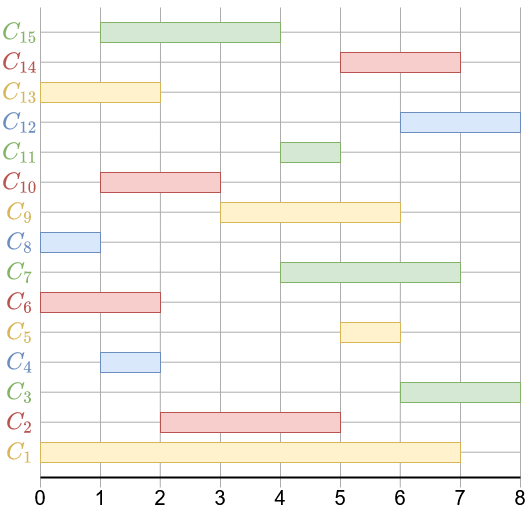
Plannings des films
C1 est un film ouzbek de 7h de contemplation des steppes d'Asie Centrale. Magnifique.

Le problème qui se pose à vous : bien sûr, vous ne pouvez voir qu'un seul film à la fois, mais vous aimeriez voir le maximum de films, tous vous intéressent autant ( surtout le film ouzbek ).
Il va donc falloir faire des choix sur la liste des films à voir : quelle est la meilleure stratégie à adopter pour cela ?

Principe

La contrainte pour que deux films soient "compatibles", est que leurs séances ne se "chevauchent" pas : par exemple, C8 et C10 sont compatibles, mais C13 et C15 ne le sont pas.
L'heure de début d'un film doit être supérieure ( ou égale, on suppose que vous pouvez passer instantanément d'une salle à une autre... ) à l'heure de fin du précédent.

Là aussi, l'étude systématique de toutes les combinaisons de films est impossible, vous allez donc adopter une stratégie gloutonne pour faire votre sélection :

La question est donc celle du critère à utiliser pour classer les films, et faire à chaque étape le meilleur choix pour le résultat global ( à savoir, voir le maximum de films ).

Plusieurs stratégies sont possibles pour classer les films :

...soit donc 6 possibilités, ça semble compliqué....heureusement, l'informatique va vous permette de résoudre votre problème !

Structure de données utilisée

Le séances seront représentées par un tuple (film, début, fin); un tableau seances contiendra l'ensemble des tuples représentant les séances.

Vous trouverez ci-dessous une fonction affiche_seances, qui permet de visualiser un ensemble de séances :

def affiche_seances(tab_seances): print("t\t:0 5 10 15 20 24") t = "" for seance in tab_seances: nom, debut, fin = seance t += nom + "\t:" + " "*debut + "#"*(fin-debut) + "\n" print(t) seances = [("C1",0,7), ("C2",2,5), ("C3",6,8), ("C4",1,2), ("C5",5,6), ("C6",0,2), ("C7",4,7), ("C8",0,1), ("C9",3,6), ("C10",1,3), ("C11",4,5), ("C12",6,8), ("C13",0,2), ("C14",5,7), ("C15",1,4)]

Tri des séances

Écrire 3 fonctions debut, fin, duree, qui serviront à trier, à l'aide de la méthode sort de Python, le tableau des séances selon les différents critères.

Tester les fonctions pour trier le tableau seances, sans oublier de tester les ordres ascendant et descendant.

def debut(seance): pass def fin(seance): pass def duree(seance): pass

SOLUTION

Implémentation de l'algorithme

Compléter le code de la fonction choix_seances ci-dessous, qui prend comme paramètres le tableau des séances trié selon un des critères ci-dessus, et qui renvoie le tableau des séances compatibles pouvant être suivies, sélectionnées grâce à l'algorithme glouton ci-dessus.

Utiliser la fonction avec les différents critères de tri possible, et visualiser le résultat : quelles stratégies sont manifestement à éliminer ?

def choix_seances(tab): """ Sélectionne les séances compatibles à suivre à l'aide de l'algorithme glouton de planning. Entrée : tab = le tableau des séances, trié selon un critère donné Sortie : le tableau des séances successives pouvant être suivies """ planning = [...] # planning = première séance t = ... # heure actuelle = heure de fin de la première séance for i in range(...): # pour chacune des séances suivantes, if ... : # si cette séance est compatible avec la précédente, ... # on l'ajoute au planning. t = ... # heure actuelle = heure de fin de la séance return planning

SOLUTION

La meilleure stratégie

Pour départager les stratégies à adopter et trouver la meilleure, vous allez utiliser votre fonction avec une liste de séances beaucoup plus conséquente.

La fonction ci-dessous génère une liste de n séances d'heure et de début aléatoire, sur une plage de 24h.

Utiliser cette fonction pour déterminer quelle est la meilleure stratégie à adopter afin de voir le maximum de films !

from random import randint def genere_intervalles(n): p = [] for i in range(1, n+1): debut = 1 fin = debut while fin <= debut: debut = randint(1, 24) fin = randint(1, 24) s = (f"C{i}", debut, fin) p.append(s) return p

SOLUTION

On montre que, en plus d'être la meilleure stratégie gloutonne, ce mode de sélection conduit à la solution optimale du planning des séances : cet algorithme est donc vraiment utilisé pour faire des plannings.

Dans le même ordre d'idée, les algorithmes gloutons se montrent efficaces pour :