NSI Première
NSI Première
Nous allons nous intéresser à un algorithme simple : celui de la recherche d'un élément de valeur donnée dans un tableau.
Un tableau au sens algorithmique est implémenté en Python avec un type construit appelé liste Python, que vous avez déjà étudié en détails ici.
En particulier, vous connaissez donc la syntaxe du test d'appartenance d'une valeur à un tableau :
if valeur in tableau:
.................
Mais on ne sait pas ce que Python fait derrière cette syntaxe pour trouver l'élément dans le tableau.
La méthode "naïve", c'est à dire qui est la plus simple, pour trouver un élément dans un tableau est la suivante :
fonction recherche_seq:
pour chaque élément successif du tableau :
si l'élément est la valeur recherchée :
alors renvoyer VRAI
fin si
fin pour
renvoyer FAUX
→ on parcourt donc le tableau élément après élément; si on trouve la valeur, on sort du parcours et de la fonction en renvoyant VRAI; si on arrive à la fin du parcours et que l'on n'a pas trouvé la valeur, on sort de la fonction en renvoyant FAUX.
Cette façon de procéder est appelée algorithme de recherche séquentielle.
Traduisez l'algorithme en codant une fonction recherche_seq.
Cette fonction prendra en argument un tableau et une valeur à chercher, et renverra True ou False selon que la valeur est présente ou non dans le tableau.
Vous testerez votre recherche sur un tableau de 50 valeurs entières entre 1 et 100 générées aléatoirement.
Modifier la fonction de façon à ce qu'elle renvoit :
Réaliser les mêmes tests que ci-dessus.
Est-ce l'algorithme utilisé par Python "en interne" pour tester l'appartenance d'une valeur dans un tableau ? Impossible de le savoir directement...mais nous allons essayer de comparer son temps d'exécution avec celui de notre algorithme "naïf".
Pour cela, nous allons utiliser le module timeit qui permet de comparer le temps d'exécution ( ou de plusieurs exécutions ) d'un script Python :
t = timeit(stmt = "code_à_éxécuter", globals=globals(), number = nombre_de_répétitions)
t1 contiendra la durée moyenne d'exécution de la recherche séquentielle, et t2 celle de la recherche "Python".Compléter le code ci-dessus avec le code des deux fonctions et un tableau de 100 valeurs aléatoires. Lancer le script plusieurs fois de suite, et comparer les valeurs de durée obtenues à chaque fois.
Que peut-on conclure ?
A conditions d'exécution identiques ( même ordinateur, même taille de données à traiter,...) tous les algorithmes ne se valent donc pas : certains sont plus efficaces que d'autre, c'est à dire qu'ils résoudront plus rapidement le problème pour lequel ils sont prévus.
On dit que leur coût en temps (ou coût temporel) est différent : un algorithme efficace aura un coût en temps plus faible qu'un autre algorithme moins efficace.
Dans le cas de notre fonction de recherche séquentielle, l'algorithme a un coût en temps plus grand que celui utilisé en interne par Python, il est donc moins efficace que ce dernier.
( Remarque : on peut aussi comparer les algorithmes en fonction de leur coût en espace, c'est à dire la plus ou moins grande quantité de mémoire dont ils ont besoin pour fonctionner; cependant nous ne nous y intéresserons pas dans ce chapitre et les suivants.)
Essayons d'analyser le coût temporel de cet algorithme, c'est à dire le nombre d'opérations élémentaires à effectuer en fonction du nombre n de données à traiter. Par exemple ici, le nombre d'opérations élémentaires à faire est le nombre de comparaisons à réaliser pour déterminer si un élément du tableau est égal à la valeur recherchée.
Nous ne pouvons pas prévoir quand cet algorithme s’arrête, mais nous pouvons dire que:
Généralement, on s’intéresse au coût au temps d'un algorithme dans le pire des cas; ici, on dira donc que le coût en temps de l'algorithme de recherche séquentielle est de n opérations élémentaires pour n données à traiter.
La complexité temporelle d'un algorithme correspond à l'évaluation du coût en temps d'un algorithme quand la quantité de données qu'il traite augmente.
Elle dépend souvent de la quantité de données notée n.
Généralement, on s'intéresse là aussi à la complexité temporelle dans le pire des cas.
Dans notre cas, le coût en temps de la recherche dans un tableau augmentera proportionnellement avec la taille du tableau : si le tableau contient 30 000 noms, le pire cas demandera
30 000 étapes; avec 60 000 noms, il y aura 60 000 étapes, etc....: le coût en temps est donc proportionnel au nombre n de données à traiter.
On dira que la complexité d'une recherche séquentielle dans un tableau est "en O(n)", ce que l'on appelle une complexité linéaire.
La notation "O(n)" ( "grand O de n" ou "O de n") est une notation mathématique qui résume la définition précédente et nous évite de dire à chaque fois : "dans le pire des cas", "proportionnel à", ...
Attention, l'étude de la complexité d'un algorithme prend du sens quand n devient très grand; pour n = 10 ou n = 20, cette notion n'a en effet pas beaucoup d'intérêt la plupart du temps car on voit alors peu de différence entre les différents algorithmes !
Mais nous ne parlons ici que de la complexité temporelle d'un ALGORITHME !
Si nous voulons savoir quelle sera la durée d'exécution du programme c'est une autre question :
La complexité temporelle d'un algorithme nous donne des indications sur le coût en temps d'un algorithme, MAIS si la complexité est théorique et ne dépend que de l'algorithme, le temps d'exécution lui est une notion pratique et dépend :
En conclusion la complexité temporelle N'EST PAS le temps d'exécution d'un programme, elle ne permet de comparer que l'efficacité d'ALGORITHMES entre eux.
Vous trouverez sur cette page un peu plus de détails sur cette notion de complexité des algorithmes.
L'algorithme de recherche d'une valeur dans un tableau est basé sur le parcours du tableau et la comparaison de chaque élément à la valeur recherchée.
Sur cette base nous pouvons imaginer des traitement différents des éléments du tableau.
Tous les algorithmes suivants étant basé sur le parcours intégral d'un tableau, leur complexité temporelle est donc O(n) dans tous les cas.
L'algorithme de recherche d'un maximum est le suivant :
fonction maximum:
maxi ← premier élément du tableau
pour chaque élément successif du tableau:
si valeur de l'élément > maxi
maxi ← valeur de l'élément
fin si
fin pour
renvoyer maximum
Vous devez coder la fonction maximum_tableau qui renvoie la valeur maximale dans un tableau.
Vous n'oublierez pas les annotations et la docstring
Tester le bon fonctionnement de votre fonction à l'aide du jeu de tests ci-dessous :
minimum_tableau renvoyant le minimum d'un tableauL'algorithme de calcul d'une moyenne est le suivant :
fonction moyenne:
somme ← 0
pour chaque élément successif du tableau:
ajouter valeur de l'élément à somme
fin pour
moyenne ← somme / n ( n = nombre d'éléments du tableau )
renvoyer moyenne
moyenne_tableau renvoyant la moyenne des éléments d'un tableau.Compléter la fonction mot_le_plus_long ci-dessous qui prend en paramètre un tableau non vide tab de mots et renvoie un tuple constitué :
En cas d'égalité entre plusieurs mots ayant la longueur maximale, on renverra celui ayant le plus petit indice.
Tester votre fonction en utilisant le jeu de tests ci-dessous :
mot_le_plus_long(['chaton', 'licorne', 'ratatouille', 'bip']) == ('ratatouille', 11)
mot_le_plus_long(['chatons', 'licorne', 'or', 'car', 'etoile']) == ('chatons', 7) # l'ordre des mots
mot_le_plus_long(['licorne', 'chatons', 'or', 'car', 'etoile']) == ('licorne', 7) # influe sur le résultat
On dispose d'un tableau contenant des valeurs entières correspondant à la hauteur de buildings placés les uns à côté des autres.
Le Soleil est situé à gauche des buildings, soit "du côté du début du tableau" :
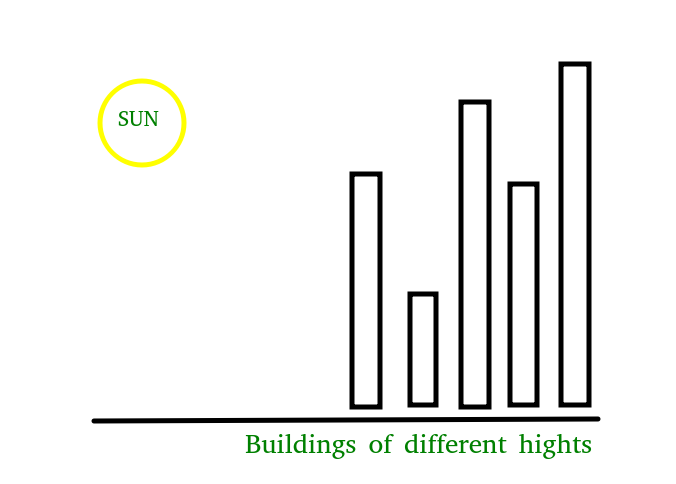
Les hauteurs des buildings ci-dessus seraient codées par le tableau : buildings = [4, 2, 5, 4, 6]
Le but est de compter le nombre de buildings au sommet desquels on verra effectivement le Soleil couchant; pour cela, la hauteur d'un building doit être strictement supérieure à celle des buildings situés à sa gauche : ainsi ci-dessus, seuls le premier, le troisième et le dernier building verront le Soleil couchant, soient les éléments du tableau aux indices 0, 2 et 4.
building_sunset, qui :
Les donnés brutes extraites d'une montre GPS se présentent sous cette forme pour chaque point enregistré :
<Trackpoint>
<Time>2021-10-17T09:58:15Z</Time>
<Position>
<LatitudeDegrees>45.5668804</LatitudeDegrees>
<LongitudeDegrees>5.9177179</LongitudeDegrees>
</Position>
<AltitudeMeters>273.1518555</AltitudeMeters>
<DistanceMeters>0.1047208</DistanceMeters>
<SensorState>Absent</SensorState>
</Trackpoint>
Nous allons simplifier cela et vous travaillerez à partir d'un tableau python contenant la durée de chaque tranche de 100 m effectuée :
[49.49, 32.37, 33.02, 33.55, 42.14, 34.6, 42.38, 32.34, 41.6, 37.03, 41.22, 37.9]
Vous devez dans cette partie coder une fonction qui renvoie le temps du meilleur 100 m.
Cette fonction prendra en argument un tableau contenant les durées de toutes les tranches de 100 m.
Pour simplifier votre travail vous trouverez ci-dessous un code qui génère un tableau à traiter pour un parcours de 10 km.
Rechercher le meilleur 100 m c'est facile, mais sur une course de 10 km cela a peu d'intérêt.
Nous allons donc tenter de rechercher le meilleur km dans le tableau précédent.
Mais sur une course de 10 km il n'y a pas que 10 fois 1 km à vérifier...comme vous pouvez le constater sur le schéma ci-dessous :
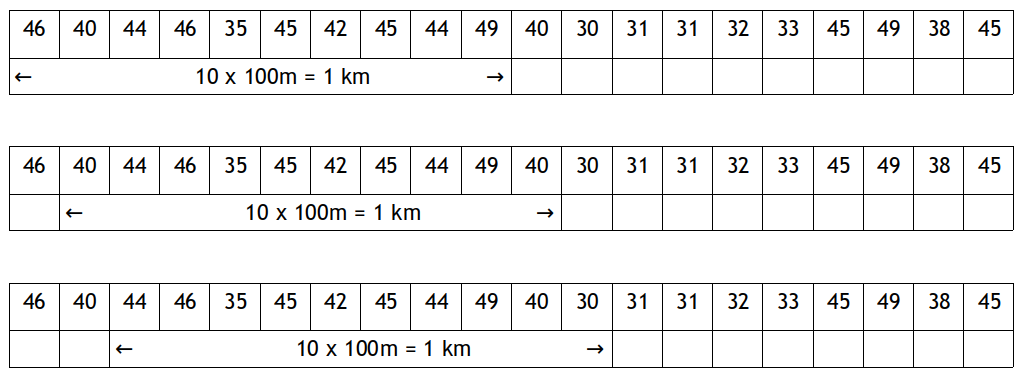
Vous devez dans cette partie coder une fonction qui renvoie le temps du meilleur km.
Cette fonction prendra en argument un tableau contenant les durées de toutes les tranches de 100 m.
Nous allons dans cette partie commencer à nous poser une question que nous reverrons en algorithmique cette année : la question de la preuve d'un algorithme.
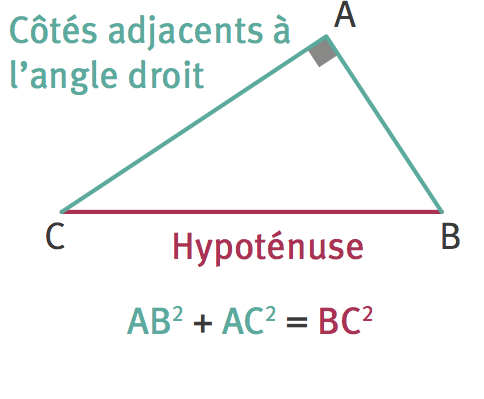
Vous connaissez le théorème ci-contre et vous savez très bien dessiner un triangle rectangle quelconque et vérifier que ce théorème est correct.
Mais vous savez aussi que ce théorème a été démontré et qu'au delà de tous les tests que l'on pourrait faire, il a été vérifié théoriquement.
Et bien c'est la même chose pour les algorithmes; on peut :
Mais il est aussi nécessaire de les démontrer.
Nous n'allons pas aujourd’hui démontrer un algorithme mais uniquement voir les deux choses qu'il faudrait démontrer...
La première chose à démontrer c'est sa terminaison, c'est à dire le fait qu'il va s'arrêter, en dehors de toute autre considération.
En effet un algorithme, la plupart du temps, effectue un grand nombre d'actions et utilise donc une boucle. Il est important de savoir si l'algorithme va s'arrêter ( sans chercher à savoir s'il remplit bien son rôle ).
Par exemple dans l'algorithme de recherche de maximum que nous venons de voir :
mettre 0 dans maximum
pour tous les éléments du tableau
si élément > maximum
mettre élément dans maximum
renvoyer maximum
On peut constater que :
Comme le tableau a nécessairement une longueur finie ( contrairement aux mathématiques, rien ne peut être infini en informatique, sauf certaines boucles mal codées...) l'algorithme va nécessairement se terminer.
Nous venons de prouver la terminaison de l'algorithme ( sans, encore une fois, avoir prouvé que celui ci nous donnait bien le maximum du tableau ).
Et cette démonstration va s'appuyer sur une notion importante : l'invariant de boucle.
En effet un algorithme, la plupart du temps, effectue un grand nombre d'actions et utilise donc une boucle.
Pour appuyer la démonstration il faut donc trouver une proposition vraie tout au long du déroulement de l'algorithme.
Par exemple dans l'algorithme de recherche que nous venons de voir :
pour tout les éléments du tableau
si l'élément est l'élément recherché
renvoyer Vrai
renvoyer Faux
Un invariant de boucle pourrait être :
"l'élément cherché est placé entre l'élément courant et la fin du tableau"
Ces notions de démonstration et d'invariant de boucle ne sont pas faciles a aborder, car, la plupart du temps, la compréhension de l'algorithme semble nous rendre inutile sa démonstration... Mais sur des algorithmes plus complexes c'est une démarche mathématique importante.
Quand on a démontré que :
On a alors réalisé une preuve mathématique de l'algorithme. On est sur de son bon fonctionnement dans n'importe quelle situation.
Il reste alors à le coder et un "bon" algorithme peut être "mal" codé, il faut donc bien faire attention, dans la phase d'implémentation, à respecter l'algorithme tel qu'il a été écrit.
Voici quelques questions pour tester si vous avez bien compris les notions de complexité et de preuve d'un algorithme.