Algorithmes de tri

Les algorithmes de tri sont un domaine très important en informatique.
Tout d'abord c'est un problème algorithmique intéressant car on connaît sa limite théorique en complexité temporelle. L'objectif est donc toujours de se rapprocher au maximum de cette limite.
Mais ce n'est pas seulement un "jeu" informatique. En effet trier des données a de nombreuses applications :

Trier des données bancaires pour pouvoir ensuite faire des transactions rapidement
Trier des chemins dans un graphe pour trouver le plus court
...

Les algorithmes de tri sont aussi très utiles aux algorithmes de recherche comme la recherche par dichotomie que l'on a déjà vue.

Tri par sélection

Principe

Tri "à la main"

se répartir par groupe de 2, et prendre un jeu de 32 cartes
disposer une dizaine de cartes sur la table, face cachée
votre objectif est de trier les 10 cartes par ordre croissant, en respectant les contraintes suivantes :

commencer le tri par le début des cartes
à un instant donné, il ne doit pas y avoir plus de deux cartes retournées.

en décomposant chaque étape, proposer alors un algorithme pour votre tri.

Algorithme

Le tri sélection est très "systématique" : il n'est pas ce que l'on ferait naturellement pour trier par exemple un jeu de cartes, mais il est très simple à mettre en œuvre par un ordinateur :

rechercher le plus petit élément du tableau, et l'échanger avec l'élément d'indice 0
rechercher le second plus petit élément du tableau, et l'échanger avec l'élément d'indice 1
...
continuer de cette façon jusqu'à ce que le tableau soit entièrement trié.

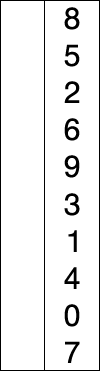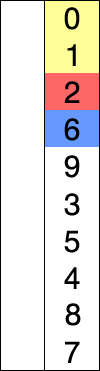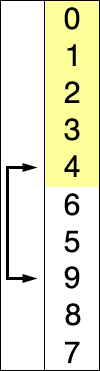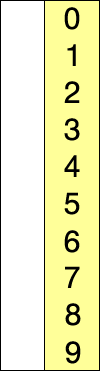
Dans l'exemple animé ci-contre, la case bleue parcours le tableau pour chercher le minimum, la case rouge correspond au minimum. Cette case rouge est ensuite déplacée pour construire la liste triée.

En gros, l'algorithme pourrait se traduire par :


pour chaque élément successif dans le tableau :
	rechercher le minimum dans la suite du tableau
	échanger ce minimum avec l’élément courant si il est plus petit que ce dernier

Plus précisément :


tri_selection(tableau t, n entier)
	Entrées	
		t est un tableau non trié
		n est la longueur de ce tableau
	Sortie
		le tableau t trié par ordre croissant

	pour i variant de 0 à n - 1
          mini ← i       
          pour j de i + 1 à n - 1
          		si t[j] < t[mini]
              		alors mini ← j
              		
          si mini est différent de i, 
          		alors échanger t[i] et t[min]
  	
  	renvoyer t

Le tri par sélection est un tri en place, ce qui signifie qu'il modifie ( = mute ) directement le tableau en entrée sans qu'il soit nécessaire d'en créer un autre.

Ceci est bien entedu possible car un tableau est justement un objet mutable; cela ne fonctionnerait bien entendu pas avec un tuple !

Répondre d'abord aux questions suivantes :

1. Repérer dans l'algorithme précédent, et indiquer ci-dessous, les lignes correspondant à la recherche de minimum. 2. A quoi correspond la variable 'mini' : un élément du tableau ? un indice dans le tableau ? autre chose ? 3. A quel cas fait référence la dernière condition ( ligne 15 ) ? 4. Pourquoi dans la deuxième boucle ( ligne 11 ), la borne inférieure est-elle 'i+1' ?

Écrire une fonction tri_selection qui implémente l'algorithme précédent en Python, et testez-la sur le tableau L généré aléatoirement en l'affichant avant et après le tri.

from random import randint def tri_selection(L): """Fonction qui trie un tableau avec l'algorithme de tri par sélection. ENTREE : L = le tableau non trié (list) SORTIE : le tableau trié (list) """ pass L = [randint(1,100) for i in range(20)]

SOLUTION

Coût

Nous allons maintenant tenter d'évaluer le coût en temps ( = complexité temporelle ) de cet algorithme.

Pour trouver un minimum dans un tableau de n éléments, il faut faire n comparaisons : la complexité en temps sera donc mesurée par le nombre total de comparaisons qu'il faudra faire pour trier entièrement le tableau.

Répondre aux questions suivantes :

1. Combien de comparaisons sont faites pour trouver le premier minimum ? 2. Combien de comparaisons sont faites pour trouver le deuxième minimum ? 3. Combien de comparaisons sont faites pour trouver le troisième minimum ? 4. Dans l'algorithme précédent, on cherche ainsi le minimum pour tous les sous-tableaux du tableau de départ. Parmi les propositions suivantes, laquelle correspond au coût en temps de l'algorithme ? (n-1) x (n-2) x .... x 1 (n-1) + (n-2) + .... + 1 n + n + n + .... + n 5. Sachant que l'expression trouvée précédemment est égale à n(n-1)/2, en déduire le coût temporel de l'algorithme de tri sélection avec la notation O()

SOLUTION

Tri par insertion

Principe

Le tri insertion est assez proche du tri que l'on met en œuvre "naturellement" si l'on doit trier un ensemble de cartes.

Tri "à la main"

se répartir par groupe de 2, et prendre un jeu de 32 cartes
mélanger le tas de cartes
trier le jeu de la manière que vous utiliseriez naturellement
en décomposant chaque étape, proposer alors un algorithme pour votre tri.

Algorithme :

On laisse le premier élément du tableau en place.
On prend le deuxième élément du tableau, si il est plus petit que le premier on l'insère à sa place, c'est à dire avant le premier.
...
On prend le i^ème élément du tableau, (la partie du tableau "à gauche" de cet élément a déjà été trié par le début de l'algorithme), et on insère alors le i^ème élément a sa place dans la partie déjà triée du tableau.

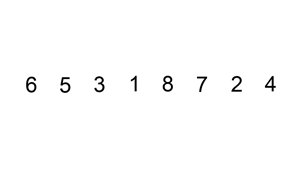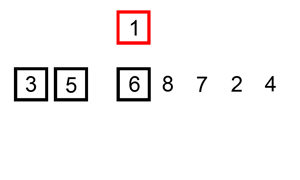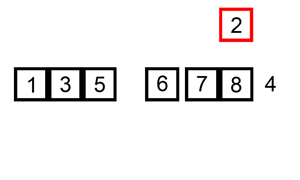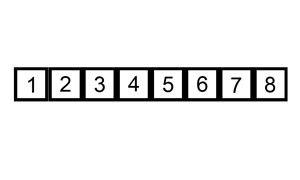
L'exemple animé ci-dessus, présente ce déroulement.

L'algorithme correspondant est donc le suivant :


pour chaque élément successif du tableau :
    venir l'insérer à sa "bonne" place dans le début de la liste triée

Pour "placer l'élément i à sa bonne place", l'idée est de parcourir le début du tableau trié ( indices 0 à i-1 du tableau ), d'y rechercher la "bonne" place, de décaler vers la droite du tableau tous les éléments suivants pour "faire de la place", et d'insérer alors l'élément dans le "trou" ainsi créé.

Dans la pratique, pour trouver la "bonne" place, on va parcourir la partie triée du tableau du haut vers le bas ( donc de i-1 à 0 ), en décalant vers la droite les éléments triés tant que l'élément à placer est plus grand que les éléments en place : quand ce n'est plus le cas, on a trouvé la "bonne" place de l'élément, et on l'insère alors.

Ce mode de fonctionnement impose que l'on garde "en mémoire" l'élément à placer car il va se faire "écraser" par ces décalages vers la droite :


tri_insertion(tableau T, n entier)
    Entrées	
        T est un tableau non trié
        n est la longueur de ce tableau
    Sortie
        le tableau t trié par ordre croissant

    pour i de 1 à n - 1:
        temp ← T[i]                     
        j ← i                               
        tant que j > 0 et T[j - 1] > temp:
            T[j] ← T[j-1]
          	décrémenter j  
        T[j] ← temp                         
	
	renvoyer T

Le tri par insertion est donc aussi un algorithme de tri en place.

Répondre tout d'abord aux questions suivantes :

1. Repérer dans l'algorithme précédent, et indiquer ci-dessous les lignes correspondant à la recherche de l'endroit ou placer l'élément courant : 2. Quelle ligne correspond à la "sauvegarde" de l'élément à déplacer ? 3. A quelle ligne précisément est réalisé le "décalage vers la droite du tableau" des éléments ? 4. A quoi correspond la ligne "décrémenter j" ( ligne 14 ) ? 5. Pourquoi dans la boucle bornée 'i' ( ligne 9 ), la borne maximum est-elle 'n-1' ?

Écrire une fonction tri_insertion qui implémente l'algorithme précédent en Python, et testez-la sur le tableau L généré aléatoirement en l'affichant avant et après le tri.

from random import randint def tri_insertion(L): """Fonction qui trie un tableau avec l'algorithme de tri par insertion. ENTREE : L = le tableau non trié (list) SORTIE : le tableau trié (list) """ pass L = [randint(1,100) for i in range(20)]

SOLUTION

Coût en temps

Nous allons maintenant tenter d'évaluer le coût en temps ( = complexité temporelle ) de cet algorithme.

A chaque étape de l'algorithme précédent, on fait des comparaison pour placer l'élément courant à sa place dans la liste déjà triée : la complexité en temps sera donc là-aussi mesurée par le nombre total de comparaisons qu'il faudra faire pour trier entièrement le tableau.

Coût dans le pire des cas

Répondre aux questions suivantes :

1. Combien de comparaisons sont faites pour trouver la place du premier élément ? 2. Combien de comparaisons sont faites pour trouver la place du deuxième élément ? 3. Combien de comparaisons sont faites pour trouver la place du troisième élément ? 4. Parmi les propositions suivantes, laquelle correspond au coût temporel de l'algorithme ? 1 x 2 x 3 x ... x (n-1) n + n + n + ... + (n-1) 1 + 2 + 3 + ... + (n-1) 5. Sachant que la relation précédente est égale à n(n-1)/2, en déduire le coût en temps de l'algorithme de tri sélection avec la notation O().

SOLUTION

Comparaison avec le tri sélection

La complexité O() établie précédemment est valable pour le pire des cas, c'est à dire un tableau complètement à l'envers : tous les éléments ont besoin d'être "déplacé" à sa bonne place.
Mais ce n'est pas toujours la situation que l'on rencontre, certains tableaux peuvent être déjà plus ou moins ordonné, qu'en est-il alors du coût en temps du tri insertion et du tri sélection ?

Pour les exemples de tableau ci-dessous ( tableau de longueur n = 9), donner le nombre de comparaisons à faire pour trier le tableau, avec l'algorithme de tri sélection ou celui de tri insertion ( vous pouvez faire ce compte à la main, ou modifier judicieusement vos codes ci-dessus pour le faire à votre place 😎...)

1. t = [9, 8, 7, 6, 5, 4, 3, 2, 1] - sélection : - insertion : 2. t = [9, 8, 7, 6, 1, 2, 3, 4, 5] - sélection : - insertion : 3. t = [1, 2, 4, 3, 5, 7, 6, 8, 9] - sélection : - insertion : 4. t = [1, 2, 3, 4, 5, 6, 7, 8, 9] - sélection : - insertion :

A partir de ces quelques exemples, discuter du coût en temps du tri sélection et du tri insertion selon le "degré de tri" d'un tableau :

Conclusion

Le tri par sélection n'est donc jamais dans la pratique utilisé...par contre, le tri par insertion est souvent utilisé après un autre algorithme plus performant, pour "peaufiner" le tri lorsque le tableau à trier devient "presque" ordonné.

Animations de différents tris — Animation montrant la vitesse d'exécution de différents algorithmes de tri dans différentes situations; on constate que le tri par sélection est systématiquement le moins rapide.
Le tri par insertion est lui plus efficace sur des tableaux *presque triés*, c'est pourquoi on l'utilise parfois en complément d'autres algorithmes pour "finir le travail" 🙂...