Du point de vue historique, le rapport de von Neumann ( "First Draft of a Report on the EDVAC" ) sorti en 1945 ( voir frise chronologique ) constitue un moment-clé, puisqu'il propose une architecture pour une machine informatique universelle et autonome, c'est à dire avec programme enregistré en mémoire, et qui peut donc réaliser des opérations diverses sans intervention d'un opérateur extérieur. Auparavant, les calculateurs étaient destinés à n'effectuer qu'un certain type bien spécifique de calculs, comme par exemple celui de trajectoires balistiques ou le décryptage de messages codés, et ne pouvaient pas être "programmées" au sens où on l'entend actuellement.
La Small-Scale Experimental Machine (SSEM), calculateur construit en Angleterre, est considéré comme la première machine basée sur l'architecture de von Neumann ayant fait tourner
un programme enregistré ( en 1948 ).
Techniquement, cette architecture a d'abord mis en jeu des tubes à vide, puis des transistors et enfin des circuits intégrés, mais c'est toujours
celle qui est utilisée dans les machines actuelles.

Les ordinateurs construits avec l’architecture de von Neumann sont constitués de quatre composants :

La particularité de cette architecture est que les programmes et les données qu'ils manipulent partagent la même mémoire; dans certaines architectures ( comme celle dite de Harvard ), programmes et données disposent au contraire de mémoires séparées.
Tous ces composants communiquent les uns avec les autres par l'intermédiaire d'un ensemble de connexions appelées bus ( en jaune sur la figure ).
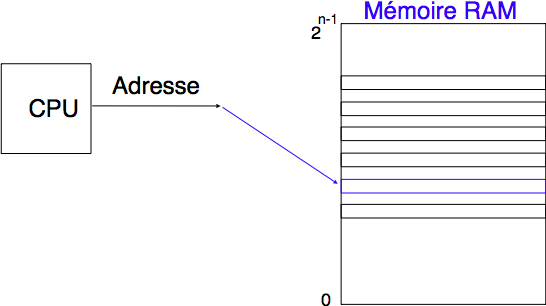
On peut se représenter la mémoire comme une série de cellules, chaque cellule étant capable de stocker 1 octet.
Chacune de ces cellules possède une adresse, exprimée sous forme de valeur numérique.
Les opérations sur la mémoire sont de 2 types : lecture / écriture. Une opération de lecture consiste à aller lire l’octet situé à l’adresse mémoire XXXXX et une opération d’écriture consiste à écrire un octet
donné à l’adresse mémoire YYYYY.
Toute donnée informatique ne peut y être représentée que par un nombre ( binaire, de surcroît...), puisque c'est la seule information qu'une machine peut traiter.
Cependant, du fait de l'architecture de von Neumann, qui stocke aussi bien programmes que données dans la même mémoire, ces nombres peuvent représenter diverses informations :
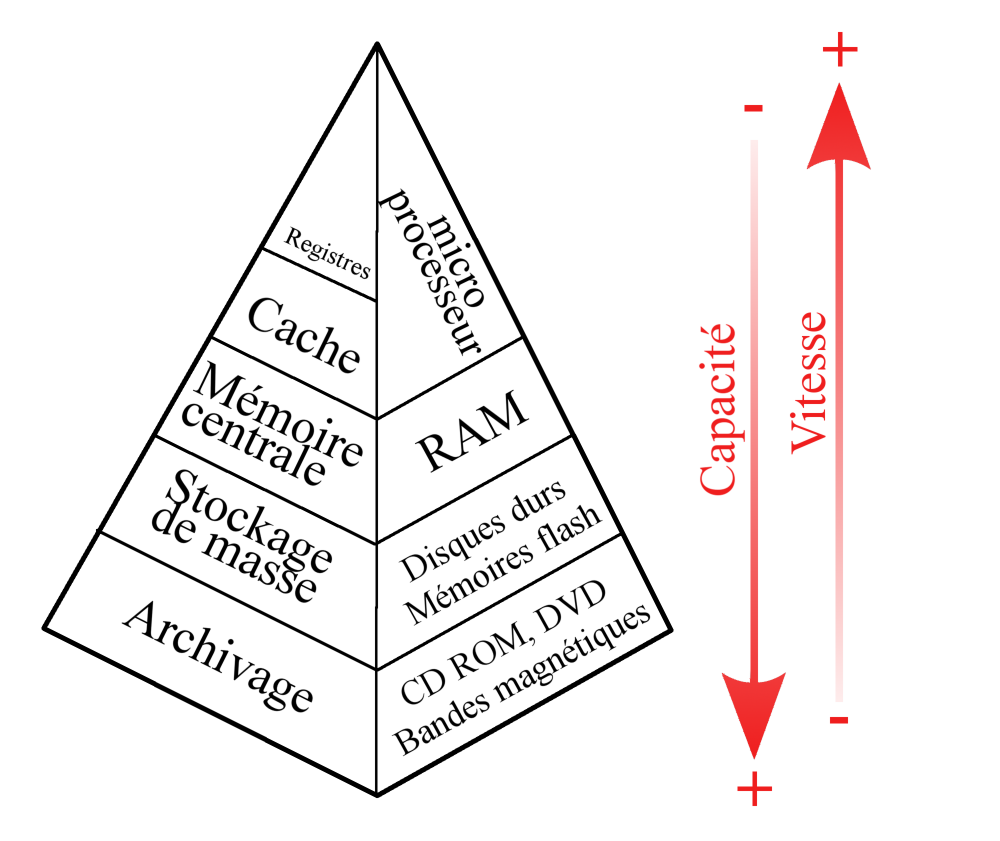
Différents types de mémoire existent dans une machine : selon les cas, le processeur peut avoir besoin d'une mémoire très rapide pour exécuter les opérations les plus courantes, ou alors de mémoires pas forcément rapides mais de grande capacité.
L'unité de contrôle est "pilotée" par une horloge très stable qui lui envoie un "top" régulièrement toutes les XXXX secondes ( ou plutôt ms, voire ns : c'est la fréquence du processeur qui indique cette durée; plus la fréquence est élevée, plus les "top" sont rapprochés dans le temps ).
Chaque "top" correspond à un "pas" de fonctionnement du microprocesseur; un pas de fonctionnement peut correspondre à une opération :
Un registre particulier du processeur, nommé compteur programme ou PC ( Program Counter ), contient l’adresse-mémoire de la prochaine instruction à exécuter ( ce qui lui permet de savoir "où il en est du programme"...); au démarrage du processeur, le registre PC est normalement initialisé à l'adresse 0, début de la mémoire, puis il est automatiquement incrémenté par l'unité de contrôle après chaque opération.
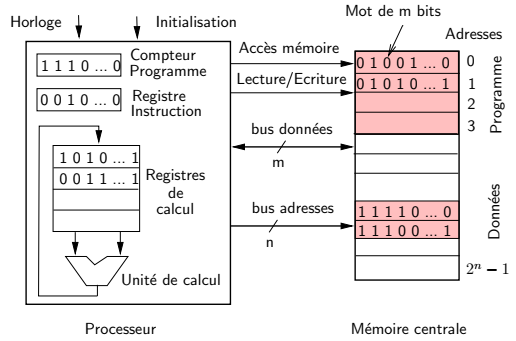
Les programmes sont donc lus linéairement par le processeur, instruction après instruction.
Le CPU a un fonctionnement cyclique :
La capacité du processeur à exécuter tous les programmes s’explique par ce fonctionnement très souple.
Un processeur donné est capable d’exécuter un certain nombre d’opérations de base, celles pour lesquelles il dispose d’un circuit électronique qui les réalise.
L’ensemble des instructions exécutables directement par le microprocesseur (instructions machines) constitue ce que l’on appelle le langage machine du processeur.

Chaque instruction machine correspond à une configuration électronique binaire composée principalement de 2 parties :
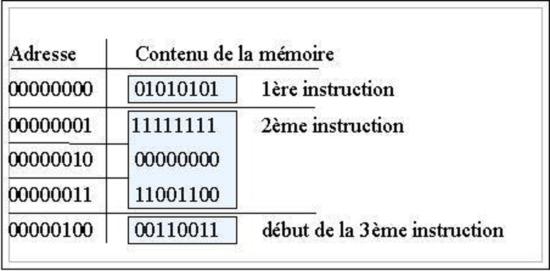
Il existe un langage machine différent pour chaque famille de processeur; la conséquence est qu'un programme écrit par exemple pour un processeur d'architecture x86-64 ( les processeurs des PC actuels ) ne s’exécutera pas sur un processeur d'architecture ARM ( utilisé par exemple dans les smartphones ) : il faudra complètement réécrire le programme !
Voila comment était programmé les premières machines : des interrupteurs, ou des connexions filaires, étaient "basculés" pour "entrer" les interminables successions de "0" et de "1" nécessaires pour réaliser la programmation; inutile de préciser le temps que cela pouvait prendre, et les innombrables erreurs que cela engendrait...
Une amélioration pour l'ergonomie du codage a été, dans les listings de programme, de remplacer les nombres binaires par des mnémoniques, courts ensembles de quelques lettres qui indiquent de manière non ambiguë le rôle de l'instruction.
Le mnémonique du code de l'opération vue dans l'exemple précédent est ainsi "ADDA"; l'instruction complète s'écrira alors : "ADDA $2".
L'assembleur n'est pas un autre langage, distinct du langage machine; c'est simplement une "traduction" pour que la compréhension humaine des programmes et leur correction devienne plus facile; bien entendu, c'est toujours des "0" et des "1" qu'il faut coder dans la machine.

Une des premières difficultés est déjà de connaître le langage machine du processeur sur lequel on veut travailler, et de devoir s'adapter en cas de changement d'architecture.
Ensuite, une des propriétés des UAL est qu'elles ne travaillent en pratique qu'avec deux opérandes.
Conséquence, on ne peut pas demander à une UAL de faire par exemple directement le calcul : 2 + 7 - 5 + 99
En effet ce calcul comporte quatre opérandes (ou quatre valeurs). Il va donc falloir décomposer le travail en demandant à l'UAL trois calculs successifs avec deux opérandes :
De plus, pour des raisons d'optimisation diverses , les valeurs des opérandes doivent être chargées explicitement dans des registres avant de faire un calcul, et la valeur du résultat devra être mémorisée explicitement dans un registre ou un emplacement mémoire; c'est ainsi par exemple par le registre A appelé accumulateur que "transitent" tous les calculs.
Par exemple, pour réaliser la simple opération d'addition suivante : R = S + 2, il faudra en fait écrire quelque chose comme :
Moralité : un processeur ne pouvant effectuer que des taches "de base", il va donc falloir en assembleur ( ou en langage machine...) décomposer au maximum le travail à faire, de façon à lui "mâcher" le travail...
Aujourd'hui, vous allez coder une machine en langage machine et en assembleur pour que vous compreniez bien ce qu'est la programmation bas-niveau, et à quoi on échappe en utilisant des langages haut-niveau comme Python !
Le programme de NSI n'exige cependant pas que vous sachiez programmer en assembleur, mais uniquement que vous soyez capables de "dérouler quelques instructions en assembleur".
L'important est que vous compreniez ce qui se passe exactement au niveau d'un microprocesseur en fonctionnement.
Programmer en langage machine/assembleur sur un PC est possible, mais compliqué...Des simulateurs logiciels existent, mais nous vous proposons d'utiliser une vraie machine, très simplifiée, dont les entrées/sorties sont visualisées grâce à des LED, exactement comme pour les premiers kits de micro-ordinateurs des années 70 qui ont lancé la vague de l'informatique personnelle ( Altair 8800 et IMSAI 8080. ).
Cette machine se nomme le Digirule 2A, se programme en langage machine ( code binaire ), et peut s' acheter pour une dizaine d'euros sur le web; vous disposez dans la salle de quelques "clones" de la machine d'origine.
Caractéristiques :


Vous l'aurez compris...il va falloir vous mettre dans la peau des pionniers de l'informatique des années 40 pour entrer les 0 et les 1 qui constitueront votre programme...
Heureusement, vous serez aidé par un simulateur, dans laquelle vous écrirez votre code en assembleur et qui vous donnera automatiquement le code binaire correspondant; vous utiliserez ce simulateur dans un premier temps pour écrire quelques programmes en assembleur, puis vous programmerez ensuite ( si vous avez le temps ) un "vrai" Digirule.
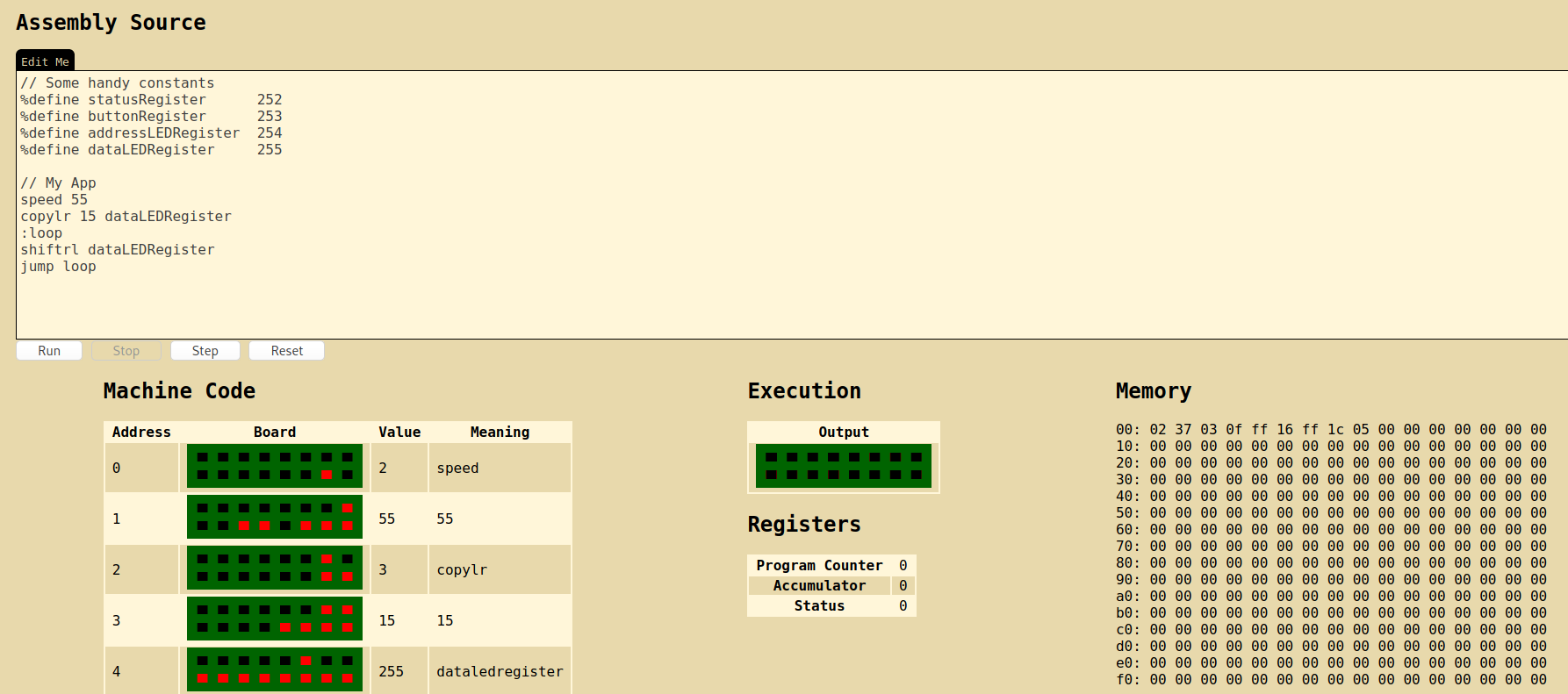
Le code entré est automatiquement traduit en langage machine en signalant les éventuelles erreurs ou omissions de données.
L'exécution du programme peut être lancée et stoppée grâce aux boutons Run et Stop; le code peut aussi être exécuté pas-à-pas avec le bouton Step.
Le bouton Reset remet à zéro le processeur en réinitialisant ses registres ( le PC est remis à l'adresse 0, soit le début du code du programme ).
Le bouton Save permet de sauvegarder le code assembleur dans un fichier.
Les instructions du langage machine du Digirule sont présentées dans ce document. Ces instructions sont en nombre réduit ( une trentaine ) mais dans un "vrai" microprocesseur, elles sont bien plus nombreuses.
Un code assembleur est déjà entré dans l'éditeur; vous pouvez l'exécuter pour voir son résultat :
// Some handy constants
%define statusRegister 252
%define buttonRegister 253
%define addressLEDRegister 254
%define dataLEDRegister 255
// My App
speed 55
copylr 15 dataLEDRegister
:loop
shiftrl dataLEDRegister
jump loop
( Vous remarquerez dans la partie Machine Code que les instructions, écrites sur une seule ligne dans l'éditeur, occupent en réalité 1, 2 ou 3 adresses mémoires.)
//( lignes 2 et 8 ) sont des commentaires : elles ne sont donc pas exécutées.%define ( lignes 3 à 6 ) permettent d'associer un nom ( = alias ) à un emplacement mémoire particulier, de façon à ne pas avoir à retenir cette adresse et pouvoir utiliser un nom plus "parlant" à sa place;
par exemple, dataLEDRegister est l'alias de l'emplacement 255 qui contient l'information affichée sur les LEDs de données.: ( ligne 11 ) est une étiquette ( ou label ) : elle permet de faire référence à un endroit du code pour pouvoir y retourner depuis un autre endroit, par exemple avec une
instruction jump ( = saut inconditionnel - ligne 13 ).Apporter des modifications au programme pour faire défiler vers la droite, partir d'un affichage différent, etc...
Voila quelques programmes en assembleur à analyser/modifier/coder selon la situation.
Il vous sera demandé de tracer l'exécution des programmes ( on dit aussi dérouler la séquence d'instructions ), c'est à dire de déterminer à chaque pas du programme le contenu de certains registres ou adresses mémoires, ou le résultat d'une opération.
Aidez-vous du document pour déterminer les instructions à utiliser et la manière de les écrire.
Quelques indications :
dataLEDRegisterVoila un code assembleur de quelques lignes :
// My App
copylr 15 20
copylr 27 21
copyra 20
addra 21
copyar 22
copyrr 22 dataLEDRegister
Status.Les premiers microprocesseurs, comme le Digirule, ne disposaient pas d'instructions pour la multiplication et la division car beaucoup plus complexes à implanter qu'un circuit additionneur. Pourtant ils étaient quand même capable de faire ces opérations ( le 4004, premier microprocesseur, a d'ailleurs été utilisé à l'origine dans une calculatrice ).
Comment faisaient-il alors ? Tout simplement, dans le cas de la multiplication, en faisant une succession d'additions : 15 x 3 = 15 + 15 + 15.
Pour cela, il faut disposer de l'analogue des boucles dans les langages de haut-niveau.
Dans le premier exemple, il y avait une boucle infinie basée sur l'instruction de saut inconditionnel jump :
:loop // étiquette de début de boucle
....... // instruction(s) à répéter
jump loop // saut inconditionnel vers l'étiquette 'loop'
Pour contrôler le nombre de "tours" de boucles, il va falloir utiliser un emplacement mémoire comme compteur; ce compteur sera décrémenté, et quand il arrivera à 0, le programme devra "sortir" de la boucle.
En assembleur, cela se présentera sous cette forme :
copylr X Y // copier la valeur X vers l'adresse Y qui servira de compteur de boucle
:loop // étiquette de début de boucle
....... // instruction(s) à répéter
decrjz Y // décrémenter la valeur à l'adresse du compteur et tester si elle est égale à 0
jump loop // saut inconditionnel vers l'étiquette 'loop'
......... // sortie de boucle ( après X tours )
L'instruction decrjz ( = Decrement Register Jump if Zero ) fonctionne ainsi : elle décrémente la valeur à l'adresse du compteur, et teste si elle devient égale à 0.
( Remarque : lorsque le résultat d'une opération vaut 0, cela est signalé par le bit 0 du registre Status, qui prend donc la valeur 1. )
Pour simplifier, on ne considérera que la division entière de deux nombres multiples l'un de l'autre.
On va suivre également un algorithme de soustractions successives; le quotient sera égal au nombre de fois que l'on doit soustraire le deuxième nombre au premier pour arriver à 0.
Pour trouver par exemple le quotient de 48 // 12 : 48 - 12 - 12- 12 - 12 = 0 → le quotient est donc égal à 4.
Il faut donc pour cela utiliser une boucle qui "tourne" jusqu'à ce qu'une valeur devienne égale à 0.
On utilisera pour cela en assembleur la structure suivante :
:loop // étiquette de début de boucle
....... // instruction(s) à répéter
bcrss 0 252 // tester si le bit 0 ( = zero bit ) du registre Status est égal à 0
jump loop // saut inconditionnel vers l'étiquette 'loop'
......... // sortie de boucle ( après X tours )
L'instruction bcrss ( = Bit Check Register Skip if Set ) teste si la valeur d'un bit donné d'un registre donné est égal à 1; comme précédemment, si ce n'est pas le cas, le programme continue normalement, sinon
l'instruction suivante est sautée.
Ici, on teste le bit "zero", qui est le LSB du registre Status, et qui est mis à 1 lorsque le résultat de l'opération précédente à donné un résultat nul, ce qui est ce qui nous intéresse ici.
Vous allez maintenant coder réellement ces programmes en assembleur, ou plutôt carrément en langage machine, sur un "vrai" Digirule...
Pour cela, vous pouvez suivre les indications de la partie "Machine Code" du simulateur, qui vous indique directement quelles LEDs doivent être éteintes ou allumées pour coder la valeur à entrer à une adresse donnée...
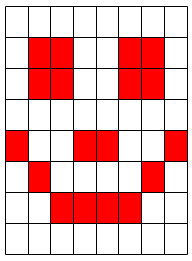
On peut exploiter le phénomène de persistance de la vision pour faire du « light-paiting », en « secouant » de bas en haut le Digirule pendant qu’il affiche très rapidement les lignes composant une image les unes à la suite des autres : une image semble se former dans l’espace, alors qu’une seule ligne de LEDs n’est "affichée" à la fois...
A vous d’écrire le programme permettant de réaliser le light-painting de l’image ci-contre ( ou une autre de votre choix !).
Des programmes sont enregistrés dans la mémoire du Digirule, notamment le célèbre « Kill the bit » ; vous pouvez le charger en tenant appuyé le bouton LOAD, et en sélectionnant le bouton D6.
D'autres applications sont disponibles...