while pour parcourir le
tableau.False, et que
l'on "basculera" à True si l'on trouve la valeur dans le tableau.while : 1) est-on arrivé à la fin du tableau, et 2 ) a-t-on trouvé la valeur.
from random import randint
def recherche_seq(tableau, valeur) :
""" Fonction qui recherche séquentiellement la présence d'une valeur dans un tableau d'entiers.
Entrées :
tableau = le tableau (list)
valeur = la valeur à rechercher (int)
Sortie :
booléen indiquant la présence ou non de la valeur dans le tableau (bool)
"""
i = 0 # indice de parcours du tableau
trouve = False # drapeau de présence ou d'absence de la valeur
while i < len(tableau) and trouve == False:
if element == valeur:
trouve = True
i += 1
return trouve
tableau = [randint(1, 100) for i in range(50)]
print(recherche(tableau, 12) # par exemple...
Ici, il est nécessaire parcourir le tableau en intégralité : une boucle for est donc mieux adaptée; et comme ce sont les indices des
éléments ayant la valeur recherché qui nous intérèsse(nt), un parcours par indice est judicieux.
from random import randint
def recherche_seq_occurrences(tableau, valeur):
""" Fonction qui recherche séquentiellement les occurrences d'une valeur dans un tableau d'entiers
Entrées :
tableau = le tableau (list)
valeur = la valeur à rechercher (int)
Sorties :
le tableau des indices des éléments ayant la valeur recherchée (list)
"""
occurrences = []
for i in range(len(tableau)) :
if tableau[i] == valeur :
occurrences += [i]
return occurrences
tableau = [randint(1,100) for i in range(50)]
print(recherche(tableau, 12) # par exemple...
from random import randint
from timeit import timeit
def recherche_python(tableau, valeur) :
return valeur in tableau # renvoi direct de l'évaluation de l'expression booléenne !
# Programme principal
tableau = [randint(1,100) for i in range(50)]
t1 = timeit(stmt = 'recherche_naive(tableau, 15)', globals=globals(), number = 1000)
print(t1)
t2 = timeit(stmt = 'recherche_python(tableau, 15)', globals=globals(), number = 1000)
print(t2)
0.001952268999957596
0.0007598840002174256
>>>
→ on constate que les durées mesurées changent d'une exécution à l'autre, mais que celle de la version Python est toujours plus petite que la version "naïve" : l'algorithme utilisé par Python doit donc être plus efficace...
def maximum(tableau):
"""
Fonction renvoyant le maximum dans un tableau d'entiers
Entrée :
tableau = tableau d'entiers (list)
Sortie :
la valeur maximale dans le tableau (int)
"""
maximum = tableau[0] # maximum initialisé à la valeur du premier élément du tableau
for element in tableau:
if element > maximum:
maximum = element
return maximum
def minimum(tableau):
"""
Fonction renvoyant le minimum dans un tableau d'entiers
Entrée :
tableau = tableau d'entiers (list)
Sortie :
la valeur minimale dans le tableau (int)
"""
minimum = tableau[0] # initialisé avec la valeur du premier élément du tableau
for element in tableau:
if element < minimum:
minimum = element
return minimum
def moyenne(tableau):
"""
Fonction renvoyant la moyenne d'un tableau d'entiers
Entrée :
tableau = tableau d'entiers (list)
Sortie :
la valeur moyenne du tableau (float)
"""
somme = 0
for element in tableau:
somme += element
return somme / len(tableau)
def mot_le_plus_long(tab):
longueur_max = len(tab[0]) # la taille du premier élément du tableau
mot_max = tab[0] # le premier élément du tableau
for mot in tab : # pour chaque mot dans le tableau
if len(mot) > longueur_max : # si le mot est plus long que le plus grand actuel
longueur_max = len(mot) # alors on stocke sa longueur
mot_max = mot # et le mot lui même
return mot_max, longueur_max # renvoi des résultats
print(mot_le_plus_long(['chaton', 'licorne', 'ratatouille', 'bip'])) # ('ratatouille', 11)
print(mot_le_plus_long(['chatons', 'licorne', 'or', 'car', 'etoile'])) # ('chatons', 7)
print(mot_le_plus_long(['licorne', 'chatons', 'or', 'car', 'etoile'])) # ('licorne', 7)
def deux_max(tab):
"""
Renvoie les deux premiers maximum ( = les deux plus grandes valeurs )
dans un tableau.
Entrée : un tableau d'entiers ( list de int ou de float )
Sortie : les deux plus grandes valeurs ( tuple de int ou de float )
"""
max1 = tab[0]
max2 = tab[0]
for valeur in tab:
if valeur > max1:
max2 = max1
max1 = valeur
elif valeur > max2:
max2 = valeur
return max1, max2
On utilise en fait ici le même algorithme que la recherche du maximum : on parcourt le tableau des buildings de gauche à droite, et à chaque fois que le maximum est modifié, cela signifie que l'on a trouvé un building "plus haut que le plus haut" rencontré jusqu'ici, c'est à dire plus grand que tous ceux situés à sa gauche : ce building verra donc forcément le Soleil; on incrémente donc le compteur des buildings face au Soleil.
def building_sunset(buildings):
"""
Renvoie le nombre de buildings qui verront le soleil.
Entrée : un tableau dont chaque élément est la taille d'un building ( list de int)
Sortie : le nombre de buildings qui voient le soleil ( int )
"""
n = 1 # compteur de buildings face au Soleil : celui situé tout à gauche verra forcément le Soleil !
h_max = buildings[0] # initialisation de la hauteur maximale courant ( celle du premier building au début )
for h in buildings:
if h > h_max:
n += 1
h_max = h
return n
def building_sunset_v2(buildings):
"""
Renvoie les indices des buildings qui verront le soleil.
Entrée : un tableau dont chaque élément est la taille d'un building ( list de int)
Sortie : le tableau des indices des de buildings qui voient le soleil ( list de int )
"""
n = [0]
h_max = buildings[0]
for i in range(len(buildings)):
if buildings[i] > h_max:
n += [i]
h_max = buildings[i]
return n
b1 = [4, 2, 5, 4, 6]
print(building_sunset_v2(b1)) # renvoie 3
print(building_sunset_v2(b1)) # renvoie [0, 2, 4]
Complexité en temps : on parcourt les n éléments du tableau dans tous les cas, la complexité est donc O(n).
On utilise ici deux boucles imbriquées :
On peut ainsi tester toutes les possibilités de profit si on vend à l'indice j après avoir acheté à l'indice i,
et on cherchera alors le maximum parmi toutes ces possibilités.
def profit_maximum(cours):
""" Fonction qui détermine le profit maximum en achetant à une date, puis en vendant à une date ultérieure
Entrée :
cours = le tableau des valeurs de l'action (list de int)
Sorties :
le profit maximum, la date d'achat et la date de vente pour obtenir ce profit ( tuple de 3 int ).
"""
profit_max = 0
achat = 0
vente = 0
for i in range(len(cours)-1): # on s'arrête à l'avant-dernier élément du tableau ( on ne peut pas acheter et vendre le même dernier jour !)
for j in range(i+1, len(cours)):
profit = cours[j]-cours[i]
if profit > profit_max:
profit_max = profit
achat = i
vente = j
return profit_max, achat, vente
Complexité en temps : plus délicat !!...
On parcourt les n-1 éléments du tableau, et pour chacun de ces éléments, on parcourt le reste du tableau : on parcourt donc globalement n x n éléments ( un peu moins en réalité, voir ci-dessous ), soit n² opérations de comparaison → la complexité est O(n²).
Plus précisément :
En tout, il faut donc parcourir : 1+2+....+(n-3)+(n-2)+(n-1); en maths, on montre que cette somme est égale à : n(n-1)/2.
→ le coût en temps est donc égal exactement à (n²-n)/2, la complexité est O(n²).
On retiendra très généralement que la présence de deux boucles imbriquées donne une complexité en O(n²) à un algorithme.
def profit_maximum_v2(cours):
profit_max = 0
achat = 0
vente = 0
for i in range(len(cours)):
if cours[i] < cours[achat]:
achat = i
else:
profit = cours[i]-cours[achat]
if profit > profit_max:
profit_max = profit
vente = i
return profit_max, achat, vente
C'est un algorithme qui revient donc à chercher en même temps le maximum et le minimum dans le tableau...
Intérêt : comme on ne parcourt qu'une seule fois le tableau, la complexité est cette fois en O(n).
On a besoin ici de déterminer DEUX valeurs différentes :
def longueur_gel(temperatures):
"""
Renvoie la durée de la plus grande période de gel, c'est à dire le plus grand nombre de jours consécutifs
où la température est restée inférieure ou égale à 0°C.
Entrée :
le tableau des températures des jours successifs ( list de int )
Sortie :
la durée de la plus longue période de gel ( int )
"""
maxi = 0 # durée de la PLUS GRANDE période de gel
l = 0 # durée d'une période de gel QUELCONQUE
for t in temperatures: # pour chaque température dans le tableau,
if t <= 0 : # si la température est négative,
l += 1 # on incrémente la durée de la période actuelle.
if l > maxi: # a-t-on trouvé une longueur plus grande que la maximum déterminé jusque là ?
maxi = l # dans ce cas, la longueur de la période actuelle devient le nouveau maximum.
else: # sinon ( sous-entendu : si la température n'est pas inférieure ou égale à 0 ),
l = 0 # alors on réinitialise le comptage de la durée de la période à 0.
return maxi
Il s'agit simplement d'une recherche de minimum dans un tableau :
def meilleur100m(L):
mini = L[0]
for hecto in L:
if hecto < mini:
mini = hecto
return mini
Plus délicat : c'est aussi une recherche de minimum, mais d'un minimum calculé à partir de 10 éléments successifs du tableau, sur toutes les "plages" possibles de 10 éléments successifs dans le tableau :
def meilleurkm(L):
minikm = 100**100 # valeur suffisamment grande pour qu'on trouve ensuite forcément une plus petite !
for i in range (len(L)-9): # attention, il faut parcourir le tableau jusqu'à 9 éléments avant le dernier sinon 'Index out of range'....
mkm = 0
for j in range(10): # boucle de calcul du temps au kilomètre, donc sur 10 éléments successifs à partir de l'indice i;
mkm = mkm + L[i+j] # revient donc à calculer : L[i+0] + L[i+1] + L[i+2] +.... + L[i+9]
if mkm < minikm: # test si le temps calculé est un nouveau minimum
minikm = mkm
return minikm
En y réfléchissant bien...on fait beaucoup de calculs inutiles : à chaque nouvelle "plage" de 10 éléments successifs, il n'y a que deux valeurs qui changent, la première et la dernière; tous les autres éléments ont été déjà inclus dans la calcul du kilomètre précédent !
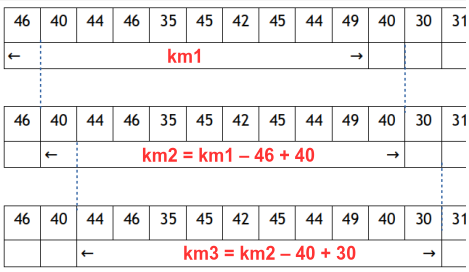
C'est donc un peu idiot de refaire totalement le calcul sur 10 éléments : il suffit en fait, à chaque nouvelle "plage", de retrancher la première valeur et d'ajouter la nouvelle au km calculé sur la "plage" précédente :
def meilleurkm_v2(L):
debut = 0 # indice de début de "plage" de calcul
fin = 9 # indice de fin de "plage" ( entre 'debut' et 'fin' inclus, il y aura toujours 10 éléments)
# initialisation du meilleur km :
# c'est, au début, celui calculé sur les 10 premiers éléments du tableau
km_min = 0
for i in range(debut, fin+1):
km_min += L[i]
km = km_min
while fin < len(L)-1: # on parcourt ensuite le reste du tableau;
km = km - L[debut] # pour calculer le nouveau km, on retranche au km précédent la première valeur,
debut += 1 # on incrémente 'debut'
fin += 1 # et 'fin' pour "avancer" la plage de calcul de 1 élément,
km = km + L[fin] # et on ajoute au calcul du nouveau km la valeur du nouvel élément en fin de "plage".
if km < km_min: # on teste alors si
km_min = km # on a trouvé un meilleur km.
return km_min
Intérêt de cette approche ?
Cette façon de faire, où l'on mémorise un calcul afin de ne pas avoir à le refaire par la suite, s'appelle programmation dynamique; cette notion est au programme de Terminale.