Algorithmes de tri

Tri par sélection

Questions sur l'algorithme

1. Les lignes correspondant à la recherche de minimum sont les lignes 10 à 13.
2. La variable mini correspond à un indice dans le tableau, pas un de ses éléments ! Après la ligne 13, mini contient l'indice du minimum du sous-tableau considéré (de l'indice i+1 à l'indice n-1
3. Les lignes 15 et 16 correspondent aux instructions pour permuter l'élément d'indice i et celui d'indice mini dans le cas où c'est nécessaire ( c'est à dire quand i != mini ).
   
4. à la ligne 11, on peut lire : pour j de i + 1 à n - 1 : ceci traduit la recherche du minimum dans la suite du tableau à partir de l'élément i, c'est à dire de i+1 à n-1.

Implémentation Python

					
from random import randint

def tri_selection(L):
    n = len(L)
    
    for i in range(0, n):       
        mini = i
        for j in range(i+1, n) : # on parcourt la partie du tableau située APRÈS l'indice i
            if L[j] < L[mini] :
                mini = j
        
        if mini != i :
            temp = L[i]
            L[i] = L[mini]
            L[mini] = temp
            # les trois lignes précédentes peuvent s'écrire aussi L[i], L[mini] = L[mini], L[i]
   
    return L

L = [randint(1,100) for i in range(20)]
print(L)
print(tri_selection(L))					
			

Coût en temps

Il n'y a ici pas de "pire cas" ou de "meilleur cas" : dans tous les cas, il faut, pour chacun des éléments, parcourir l'intégralité du reste du tableau :

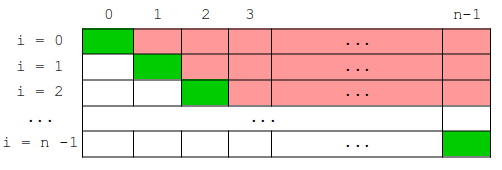
→ on fait donc en totalité : (n-1) + (n-2) + (n-3) + .... + 0 comparaisons = n(n-1)/2 = (1/2)(n²-n).

Pour de grandes valeurs de n, cette expression tend vers n² : cet algorithme est donc de complexité O(n²) ( = quadratique ).

Tri par insertion

Questions sur l'algorithme

1. Les lignes correspondant à la recherche de l'endroit ou placer l'élément courant sont les lignes 10 à 14.
2. On sauvegarde l'élément à déplacer avant de trouver sa place à la ligne 10; on le place à la "bonne" place à la ligne 15.
3. On réalise le "décalage vers la droite du tableau" des éléments à la ligne 13.
4. La ligne "décrémenter j" ( ligne 14 ) correspond au "déplacement vers la gauche du tableau" lors de la recherche de la place de l'élément courant.
5. Dans la boucle i ( ligne 9 ), la borne maximum est n-1 car le premier élément du tableau est indicé "0" donc le dernier est indicé "n-1".

Implémentation

def tri_insertion(L):
    for i in range(1, len(L)):
        
        temp = L[i]
        j = i
        
        while  j > 0 and L[j-1] > temp:
            L[j] = L[j-1]
            j = j-1 
        L[j] = temp	# on insère l'élément à sa "bonne" place
    
    return L						
						

Coût en temps

Dans le pire des cas, la "bonne place" de chaque élément est le tout début ( indice 0 ) du tableau ( le pire des cas pour cet algorithme est donc un tableau qui est initialement trié dans l'ordre décroissant ).

Dans ce pire des cas, on doit alors faire, pour trouver la "bonne place" de chaque élément :

• Pour i = 1 : j varie de 1 à 0 soit 1 décalage
• Pour i = 2 : j varie de 2 à 0, soit 2 décalage
• Pour i = 3 : j varie de 3 à 0, soit 3 décalage
• ...
• Pour i = n - 1 : j varie de n-1 à 0, soit n-1 décalages

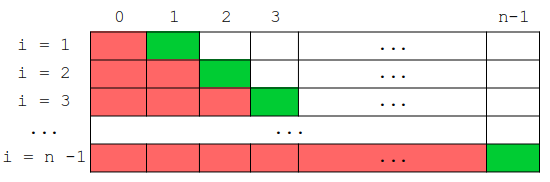
→ on fait donc en totalité : 1 + 2 + 3 + ... + (n-1) décalages = n(n-1)/2 = (1/2)(n²-n).

Pour de grandes valeurs de n, cette expression tend vers n² : cet algorithme est donc (aussi) de complexité O(n²) ( = quadratique ).

Mais la complexité s'entend dans le pire des cas; or, dans le tri par insertion, on arrête le "parcours à rebours" de la partie triée du tableau dès que l'on a trouvé la place où insérer l'élément courant; la position de cette place n'est pas forcément au tout début de la partie triée, ce qui fait que ce parcours ne concerne parfois qu'un petit nombre d'éléments, surtout si le tableau est d'origine déjà un peu trié : en moyenne, le tri par insertion a donc un coût en temps qui est meilleure que le tri par sélection...