TP Parcours de graphe

Un problème de labyrinthe

On peut considérer un labyrinthe comme un ensemble de "cases" dans une grille; une case "vide" indique par exemple un passage, alors qu'une case "pleine" indique un mur :

Un labyrinthe est le plus souvent représenté sous forme d'un tableau de tableaux en mémoire , chaque case étant à l'intersection d'une ligne et d'une colonne de cette grille :


# '0' = case vide / '1' = mur )
laby = [
    [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], 
    [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1], 
    [1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1], 
    [1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1], 
    [1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1], 
    [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], 
    [1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], 
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1]
]

Le parcours d'un labyrinthe pour en trouver la sortie peut alors être fait en utilisant par exemple la récursivité ( avec les limites que l'on connaît pour les très grands labyrinthes ).

Pour ce projet cependant, on utilisera une approche purement "relationnelle" : le labyrinthe sera modélisé par un graphe, où les cases vides représentent les sommets du graphe, et le fait que deux cases "vides" sont reliés entre elles correspondra à l'existence d'une arête entre ces deux sommets.

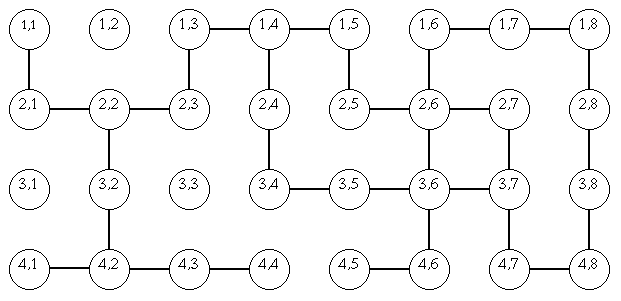
Trouver la sortie d'un labyrinthe revient donc à chercher un chemin dans le graphe entre le "sommet d'entrée" du labyrinthe et le "sommet de sortie".

Modélisation du labyrinthe

Vous pourrez utiliser la classe Graphe pour modéliser le labyrinthe en l'implémentant sous forme de liste d'adjacence.

Cependant attention, un sommet ne sera pas désigné par un simple caractère mais sera étiqueté par un tuple contenant les coordonnées ( ligne, colonne) dans la grille de la case correspondant à ce sommet ( cf. image ci-dessus ).

C'est un travail un peu compliqué, mais une fois le graphe créé, il sera très facile de s'en servir pour trouver la sortie du labyrinthe...

Écrire une fonction cree_graphe() qui prend comme paramètre le tableau de tableaux laby et crée le graphe modélisant le labyrinthe.

En parcourant le tableau de tableaux passé comme argument, cette fonction devra créer les sommets du graphe mais également les relations qui existent entre deux cases lorsque celles-ci communiquent ( c'est à qu'elles sont adjacentes ).
Ces relations devront a priori être à double sens ( graphe non orienté ).

Pour vérifier que le graphe créé est correct, vous pourrez afficher son dictionnaire de listes d'adjacence, ou utiliser la méthode dessiner de la classe Graphe si vous l'aviez implémentée.

from graphe import Graphe def cree_graphe(laby: list)->Graphe: """Fonction qui crée le graphe modélisant un labyrinthe décrit par un tableau de tableaux. Entrée: laby = tableau de tableaux modélisant le graphe - Codage : 0 = case vide / 1 = mur Sortie : un objet de type Graphe modélisant le graphe. Chaque sommet y est désigné par un tuple (ligne, colonne) dans le labyrinthe """ pass # '0' = case vide / '1' = mur ) laby = [ [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1] ]

SOLUTION

Trouver la sortie du labyrinthe

La question : à partir de l'entrée du labyrinthe, quel chemin suivre pour atteindre la sortie ( pas forcément le plus court...) ?

C'est un problème classique pour lequel plusieurs techniques sont possibles pour une personne se trouvant à l'intérieur du labyrinthe.

Mais nous avons la chance d'avoir le plan du labyrinthe ! Laissons alors l'ordinateur déterminer la sortie à notre place...

Écrire une fonction resoudre() qui prend comme paramètre le graphe modélisant le labyrinthe, le sommet d'entrée et le sommet de sortie, et qui détermine le chemin à suivre pour sortir du labyrinthe depuis le sommet d'entrée jusqu'au sommet de sortie ( qui doivent bien entendu être dans le graphe...).

La fonction renverra le chemin à suivre sous une forme à déterminer (liste des sommets à suivre par exemple ).

from graphe import Graphe def cree_graphe(laby: list)->Graphe: # Code précédent pass def resoudre(g: Graphe, depart: tuple, arrivee: tuple)->list: """Fonction qui détermine le chemin à suivre pour sortir d'un labyrinthe. Entrée: g = graphe modélisant le labyrinthe depart = tuple (ligne, colonne) représentant le sommet de départ arrivee = idem pour le sommet d'arrivée Sortie : la liste des sommets à suivre pour aller du sommet de départ à celui d'arrivée """ pass # '0' = case vide / '1' = mur ) laby = [ [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1] ]

Attention à la manière dont est représenté chaque sommet ( un tuple ) dans le graphe.

Vérifier que la fonction donne le bon résultat !! ( facile à déterminer sur le graphe en exemple...)

SOLUTION

Affichage et visualisation du chemin à suivre

La méthode imshow du module Matplotlib.pyplot permet d'afficher une matrice "2D", avec des couleurs différentes selon la valeur des éléments de la matrice : c'est tout à fait ce qu'il nous faut pour visualiser le résultat de la recherche de parcours de sortie !

Écrire une fonction affiche qui :

prend comme paramètres la matrice représentant le labyrinthe et la liste des sommets à suivre de l'entrée à la sortie du labyrinthe.
modifie la matrice ( ou sa copie...) de manière à placer la valeur 2 dans les éléments correspondants aux cases du parcours à suivre
utilise la méthode imshow pour afficher le labyrinthe et son chemin de sortie.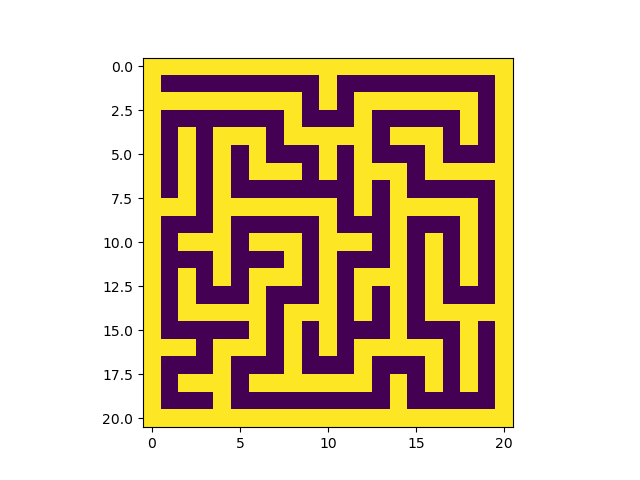

import matplotlib.pyplot as plt from graphe import Graphe def cree_graphe(laby: list)->Graphe: # Code précédent pass def resoudre(g: Graphe, depart: tuple, arrivee: tuple)->list: # Code précédent pass def affiche(laby: list, chemin: list)->None: """Fonction qui affiche le labyrinthe et le chemin de sortie. Entrées: laby = le tableau de tableaux représentant le labyrinthe chemin = la liste des sommets à suivre pour sortir du labyrinthe Sortie: Aucune """ pass plt.imshow(laby) plt.show() # '0' = case vide / '1' = mur ) laby = [ [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1] ]

SOLUTION

Prolongement possible

Les fichiers textes ci-dessous contiennent la description de quelques labyrinthes selon le codage suivant : 0 = case vide, 1 = mur, 4 = entrée, 5 = sortie.
Une case correspond à un caractère de chaque ligne.

laby0.txt, laby1.txt, laby2.txt

Écrire une fonction qui extrait les informations de ces fichiers pour en tirer le tableau de tableaux représentant le labyrinthe, puis utiliser les fonctions précédentes pour résoudre le labyrinthe !

SOLUTION

Créer des labyrinthes

De très nombreux algorithmes existent pour générer des tableaux de tableaux représentant un labyrinthe; en voici un qui produit des labyrinthes parfaits, c'est à dire dont chaque case est relié à une autre par un unique chemin.

Il utilise un parcours de graphe en profondeur avec retour en arrière ( backtracking ) :

on part d'un labyrinthe ne contenant que des murs
à partir d'une case donnée, l'algorithme crée aléatoirement un chemin en "cassant" des murs, tant qu'il peut trouver des cases encore non explorées
si il n'y a plus de case non explorée au bout du chemin, l'algorithme "revient en arrière" au début du chemin, et recherche un nouveau chemin à partir de là, y créant donc une "intersection" dans le labyrinthe
si toutes les cases du labyrinthe ont été explorées, l'algorithme s'arrête...

Cet algorithme suppose de garder la trace des cases déjà explorées, ainsi que celle des débuts de chemins, afin d'y revenir au besoin ("backtracking" ).

Même si l'algorithme ressemble à un parcours de graphe, il n'est pas nécessaire de créer un graphe à proprement parler : c'est le tableau de tableaux qui sera directement modifié.


fonction creer_laby(s: sommet courant):
	
	ajouter s à la liste des cases déjà explorées
   
	si il y a des cases accessibles depuis s et pas encore explorées:
		en prendre une au hasard
		casser le mur entre elle et s
		ajouter s à la liste des débuts de chemin
		appeler récursivement la fonction creer_laby à partir de la nouvelle case
	sinon:
		extraire le dernier début de chemin de la liste des débuts ( si il en reste un )
		appeler récursivement la fonction creer_laby à partir de lui

Le plus délicat est de déterminer les cases accessibles depuis une case donnée.

Écrire une fonction creer_laby qui implémente l'algorithme ci-dessus pour générer un tableau de tableaux représentant un labyrinthe, et l'afficher ensuite.

Le tableau initial ne contenant que des murs est déjà donné, pour un nombre de lignes et de colonnes modifiables.

Les murs sont en jaune, les cases vides en violet.

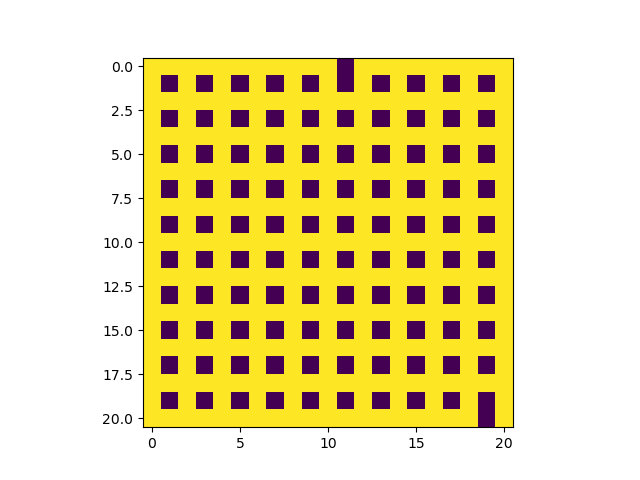
L'entrée et la sortie du labyrinthe sont placées et peuvent être modifiées.

Le point d'entrée de l'algorithme pourra être n'importe quelle case vide ( pas un mur évidemment ), pas forcément l'entrée ou la sortie.

from random import randint, shuffle # à utiliser au besoin import matplotlib.pyplot as plt # pour l'affichage du labyrinthe def creer_laby(laby: list[list], s: tuple[int, int], visites: list, debuts: list)->list[list]: '''Fonction qui créé un tableau de tableaux représentant un labyrinthe, à l'aide de l'algorithme de parcours en profondeur avec retour en arrière. Entrées : laby = le tableau de tableaux représentant le labyrinthe, ne contenant que des murs au premier appel s = la case courante visites = la liste des cases déjà explorées débuts = la liste des débuts de chemin Sortie: le tableau de tableaux modifié ''' pass # Dimensions du labyrinthe H = 10 L = 10 # labyrinthe ne contenant que des "murs": laby = [[0 if i%2!=0 and j%2!=0 else 1 for j in range(2*L+1)] for i in range(2*H+1)] # entrée et sortie du labyrinthe ( peuvent être déplacées ) laby[0][1] = 0 # entrée laby[2*H][2*L-1] = 0 # sortie debut = (1, 1) # point d'entrée de l'algorithme ( peut être modifié ) laby = creer_laby(laby, debut, [], []) plt.imshow(laby) plt.show()

SOLUTION

Résolveur automatique du problème des seaux

Dans le problème des seaux "original", il est assez facile de déterminer le chemin à suivre pour aller du sommet (0, 0) au sommet (4, 0), car les deux seaux ont des contenances maximales assez faibles ( 5L et 3L ); qu'en serait-il avec des seaux de contenances beaucoup plus grandes, disons 15L et 7L ? Combien d'étapes seraient nécessaires pour aboutir par exemple à une situation correspondant au sommet (11, 0) ? Et d'abord, existe-t-il même une solution ??

La modélisation "automatique" du graphe correspondant au problème permettrait de s'affranchir de ce travail "à la main", en laissant l'ordinateur déterminer le chemin à suivre si celui-ci existe !

Modélisation du problème par un graphe

Plutôt que de se concentrer sur un problème particulier, vous allez même écrire un script qui permette la résolution du problème pour n'importe quelles contenances de saut, que vous stockerez par exemple dans deux variables S1 et S2.

Toute la difficulté sera de créer les relations qui doivent exister entre les sommets pour respecter les contraintes du problème, et seulement celles-ci.

Écrire une fonction cree_graphe qui :

crée les sommets du graphe sous forme de tuples (v1, v2) représentant toutes les situations possibles pour les volumes v1 et v2 des deux seaux, avec : 0 ≤ v1 ≤ S1, et 0 ≤ v2 ≤ S2.
crée les arcs ( a priori, certaines relations ne se feront que dans un sens ) modélisant les relations qui correspondent à des "transitions permises" d'un sommet à un autre du graphe selon les contraintes du problèmes ( on ne peut que vider ou remplir au maximum un des seaux, aucun instrument de mesure plus précis n'étant disponible ).

Pour créer ces arcs, on parcourra tous les sommets du graphe, et pour chacun d'entre eux, on se posera la question : avec quel(s) autre(s) sommet(s) doit il y avoir une relation ?

Pour ne rien oublier, voila les "catégories" de relations à modéliser :

remplir un des deux seaux en laissant le contenu de l'autre inchangé
vider un des deux seaux et laisser le contenu de l'autre inchangé
transvaser ( si possible ) complètement le contenu d'un des seaux dans l'autre si ce dernier est vide
transvaser une partie d'un des deux sauts pour remplir l'autre quand c'est possible.

C'est clairement la dernière catégorie la plus délicate à modéliser; bien réfléchir à :

la condition que doit vérifier v1 ( respectivement v2 ) par rapport à S2 et v2 ( respectivement S1 et v1 ) pour qu'un transvasement soit possible du seau 1 pour remplir le seau 2 ( respectivement du seau 2 pour remplir le seau 1 )
le volume qu'il faut alors transvaser, en fonction de v1, S2 et v2 ( respectivement v2, S1 et v1 )

En déduire alors entre quels sommets du graphe il faut créer un arc.

from graphe import Graphe # Constantes à modifier pour changer de situation S1 = 5 S2 = 3 def cree_graphe(S1: int, S2: int)->Graphe: """Fonction qui créé le graphe associé au problème des seaux ( création des sommets et des arcs ). Entrées : S1 = contenance du seau 1 S2 = contenance du seau 2 Sortie : un objet de type Graphe modélisant le problème. """ pass

SOLUTION

Résolution du problème

La résolution du problème des seaux va donc consister à rechercher le chemin à suivre pour aller du sommet (0, 0) du graphe à un sommet donné.

Écrire une fonction resoudre qui prend en paramètre le graphe associé au problème et le sommet d'arrivée, et qui renvoie les étapes à suivre ( sous forme de chaîne de caractères par exemple ), correspondant au chemin dans le graphe pour résoudre le problème.

On pourra éventuellement dans un premier temps, déterminer si un chemin existe effectivement.

from graphe import Graphe # Constantes à modifier pour changer de situation S1 = 5 S2 = 3 def cree_graphe(S1: int, S2: int)->Graphe: # Code ci-dessus pass def resoudre(g: Graphe, s: tuple)->str: """Fonction renvoyant le chemin à suivre pour résoudre le problème des seaux. Entrée: g = le graphe modélisant le problème s = le sommet d’arrivée Sortie: la chaîne de caractères indiquant les étapes à suivre pour résoudre le problème. """ pass

Pour tester la fonction, on rappelle que pour le problème original (S1 = 5 et S2 = 3), le chemin à suivre pour arriver à un seau contenant 4L est :


'(0, 0) -> (5, 0) -> (2, 3) -> (2, 0) -> (0, 2) -> (5, 2) -> (4, 3) -> (4, 0)'

Pour la situation où S1 = 15 et S2 = 7, voila le chemin à suivre pour aller au sommet (11, 0) 😥 :


'(0, 0) -> (15, 0) -> (8, 7) -> (8, 0) -> (1, 7) -> (1, 0) -> (0, 1) -> (15, 1) -> (9, 7) -> (9, 0) -> (2, 7) -> (2, 0) -> (0, 2) -> (15, 2) -> (10, 7) -> (10, 0) -> (3, 7) -> (3, 0) -> (0, 3) -> (15, 3) -> (11, 7) -> (11, 0)'

SOLUTION

Prolongement possible

Rajouter une fonctionnalité qui permette de calculer le nombre d'étapes pour arriver à la solution du problème.

Résolution d'un jeu de réflexion

De nombreux petits jeux de réflexion peuvent être résolus grâce à la théorie des graphes et de leur parcours, dans la mesure où il s'agit souvent d'aller d'un état donné du jeu à un autre, en passant par des états intermédiaires : chaque état du jeu peut alors représenter un sommet d'un graphe, et le passage d'un état à un autre les relations entre ces sommets.

La recherche d'un chemin dans ce graphe permet alors de déterminer l'enchaînement des différents états qui permet de résoudre le jeu.

Voila par exemple le célèbre jeu de réflexion Loup-Chèvre-Chou, qui fait partie de la catégorie des "problèmes de passage de rivière" :

Un berger, en compagnie d’un loup, de sa chèvre et d’un chou sur une rive, veut traverser une rivière.
Pour cela, il dispose d’une petite barque qui ne peut contenir que lui et un autre objet ou animal.
De plus, si la chèvre et le chou sont ensemble sur une rive quand le berger s’éloigne, la chèvre mange le chou. Et si le loup et la chèvre sont ensemble quand le berger s’éloigne, le loup mange la chèvre !

Comment faire pour que tout le monde traverse sans problème ?

Représentation du problème

Il faut se poser la question de comment représenter la situation : on peut par exemple convenir que chaque état du jeu sera représenté par une chaîne de 3 caractères, telle que :

le premier caractère indique la rive où se trouve le loup, le deuxième la chèvre, le troisième le chou
un caractère '0' indique la rive gauche, un caractère '1' la rive droite

( Si vous préférez utiliser un autre codage de votre choix, help yourself ! )

Au début du problème, l'état du jeu est donc '000'; il s'agit donc de parvenir à l'état '111' en suivant les règles du jeu, c'est à dire trouver l’enchaînement des états '010', '110', etc.. permis par le jeu.

Modélisation par un graphe

Chaque état du jeu représentera un sommet d'un graphe. Ces sommets ne sont pas en très grand nombre, ce qui fait que la résolution de ce problème pourrait se faire à la main...mais nous allons laisser Python réfléchir à notre place...

Mais il va falloir mettre à l'épreuve ses capacités d'abstraction !

Combien de sommets le graphe contiendra-t-il ? Sera-t-il orienté ou pas ?
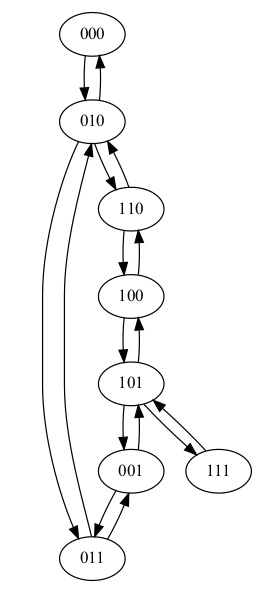
Dans un premier temps, on créera tous les sommets que peut avoir le graphe modélisant le problème, sans se soucier des relations entre eux.
Écrire le code qui permet de créer un graphe avec la liste de ses sommets, sommets dont l'étiquette sera la chaîne de caractères représentant un état du jeu.

Pour "automatiser" cette création, on pourra se servir de la fonction bin() qui renvoie la représentation binaire d'un nombre entier; le résultat est sous la forme d'une chaîne '0bXX', il faudra donc retirer les caractères '0b' du début. De plus, pour faire en sorte que chaque code fasse bien 3 caractères, on pourra utiliser la méthode de chaîne zfill(n) qui permet de rajouter n caractères '0' au début de la chaîne à partir de laquelle elle est appelée.
Intéressons-nous ensuite aux relations entre ces sommets : une relation représentera un passage "permis" ( par les règles ) entre un état du jeu et un autre; pour chaque sommet, on ne créera donc une relation avec un autre que si les conditions suivantes sont réunies :
- il ne faut pas créer de relation entre un sommet et lui-même ( pas de boucle dans ce graphe )
- un seul objet ou animal peut traverser à la fois ( en plus du berger ) : il ne faut donc pas créer de relation entre deux sommets dont les étiquettes ont plus d'un caractère de différence, ce qui signifierait qu'on a fait changer de rive plus d'un objet/animal à la fois.
- enfin, il ne faut pas créer de relation entre deux sommets qui correspondent à deux états où soit le loup et la chèvre restent ensemble sur la même rive, soit la chèvre et le chou restent ensemble sur la même rive ( attention, cela ne veut pas dire que ces états sont "interdits", mais qu'ils ne doivent pas rester ainsi lors du passage à un autre état : on peut par exemple amener le loup et la chèvre sur la même rive, et repartir avec un des deux ).
  Bien réfléchir aux codes des états correspondant à ces situations, et ne pas créer de relation entre les sommets correspondants.
Là aussi, la création des relations peut être tout à fait automatisée.

Résolution du problème

A l'aide de vos connaissances, et notamment du travail réalisé au chapitre précédent, déterminer dans le graphe établi précédemment un chemin permettant de résoudre le problème ( il existe en réalité deux solutions. )