Implémentation Python des algorithmes de parcours de graphes

Algorithmes BFS et DFS

Vous allez maintenant implémenter les algorithmes vus au chapitre précédent.

Préalablement, il faudra que vous disposiez des ressources vous permettant de gérer un graphe bien sûr, mais également les structures de données ( pile et file ) nécessaires aux parcours.

Pour les graphes : une implémentation sous forme de matrice d'adjacence serait mal adaptée ( pourquoi ?? )...
Pour la file : vous avez plusieurs possibilités, qui utilisent toutes le paradigme de programmation objet :
- soit utiliser une implémentation réalisée par vous-même ( liste Python, qui présente des limitations en terme d'efficacité, même si a priori ici, les files ne seront jamais très grandes , ou version file avec deux piles que vous aviez faite en exercice, ou file circulaire, optimisée, etc...)
- la classe deque, que vous avez déjà utilisée pour le parcours en largeur des arbres.
Pour la pile : là-aussi, plusieurs solutions :
- une classe écrite par vous-même, qui utilise une liste Python ou une liste chaînée ( donc de bonne efficacité puisque n'utilisant que les méthodes de liste Python pop() et append() qui sont en O(1). )
- la classe deque

Les deques sont une généralisation des piles et des files ( deque se prononce "dèque" et est l'abréviation de l'anglais double-ended queue) : il est possible d'ajouter et retirer des éléments par les deux bouts des deques. Celles-ci gèrent des ajouts et des retraits utilisables par de multiples fils d'exécution (thread-safe) et efficaces du point de vue de la mémoire des deux côtés de la deque, avec approximativement la même performance en O(1) dans les deux sens.

Il faut importer la classe deque à partir du module collections :


from collections import deque

Pour créer une deque vide :


pile = deque() # ou file = deque() bien sûr...

Il existe plusieurs méthodes pour ajouter/retirer des éléments à chaque "extrémité" d'une deque :

	A gauche	A droite
insertion d'un élément	`appendleft(x)`	`append(x)`
suppression et renvoi d'un élément	`popleft()`	`pop()`

Chaque extrémité d'une deque étant parfaitement équivalente en terme de complexité, à vous de choisir les méthodes adaptées pour la gestion de votre file ou de votre pile.

Enfin, la fonction len() peut être appliquée à une deque pour déterminer le nombre d'éléments qu'elle contient.


len(pile) # renvoie le nombre d'éléments dans la deque

Dans un script qui importe tous les modules nécessaires, écrire le code des fonctions suivantes, puis les tester sur les graphes donnés en exemple.

Ici, "traiter un sommet" consistera soit à simplement afficher son étiquette, soit à remplir ( par exemple ) un tableau avec les étiquettes des sommets, tableau qui sera renvoyé en fin de parcours pour visualiser celui-ci.

Du parcours de graphe en profondeur d'abord récursif :

Attention à la nécessité de passer comme paramètre la structure de données gardant la trace des sommets déjà visités; étant mutable, cette structure devra être initialisée en dehors de la fonction.

def DFS_recursif(G, u, visites): """ Traite les sommets d'un graphe dans l'ordre de son parcours en profondeur récursif. Entrées : G = le graphe u = le sommet courant ( = départ du parcours au premier appel ) visites = structure de données ( list ou dict ) stockant les sommets déjà visités ( initialisée en dehors de la fonction ) Sortie : aucune, ou le parcours ( list ) """ pass directed = {"A":["C", "D"], "B":["K"], "C":["E"], "D":["C", "E", "G"], "E":["B"], "F":["G"], "G":["E", "H", "J"], "H":[], "I":["F"], "J":["I"], "K":["H", "I"] } undirected = {"A":["C"], "B":["E", "K"], "C":["A", "D"], "D":["C", "E", "F", "G"], "E":["B", "D", "G"], "F":["D", "G", "I"], "G":["D", "E", "F", "H", "J"], "H":["G", "K"], "I":["F", "J", "K"], "J":["G", "I"], "K":["B", "H", "I"] }

Du parcours de graphe en profondeur d'abord ( DFS ) itératif :

Attention à marquer le sommet de départ comme visité avant le parcours des autres sommets.

#from collections import deque #from pile import * def DFS_iteratif(G, s): """ Traite les sommets d'un graphe dans l'ordre de son parcours en profondeur itératif. Entrées : G = le graphe r = le sommet de départ du parcours Sortie : aucune, ou le parcours ( list ) """ pass directed = {"A":["C", "D"], "B":["K"], "C":["E"], "D":["C", "E", "G"], "E":["B"], "F":["G"], "G":["E", "H", "J"], "H":[], "I":["F"], "J":["I"], "K":["H", "I"] } undirected = {"A":["C"], "B":["E", "K"], "C":["A", "D"], "D":["C", "E", "F", "G"], "E":["B", "D", "G"], "F":["D", "G", "I"], "G":["D", "E", "F", "H", "J"], "H":["G", "K"], "I":["F", "J", "K"], "J":["G", "I"], "K":["B", "H", "I"] }

Du parcours de graphe en largeur d'abord ( BFS ) :

#from collections import deque #from file import * def BFS(G: Graphe, s): """ Traite les sommets d'un graphe dans l'ordre de son parcours en largeur. Entrées : G = le graphe s = le sommet de départ du parcours Sortie : aucune, ou le parcours ( list ) """ pass directed = {"A":["C", "D"], "B":["K"], "C":["E"], "D":["C", "E", "G"], "E":["B"], "F":["G"], "G":["E", "H", "J"], "H":[], "I":["F"], "J":["I"], "K":["H", "I"] } undirected = {"A":["C"], "B":["E", "K"], "C":["A", "D"], "D":["C", "E", "F", "G"], "E":["B", "D", "G"], "F":["D", "G", "I"], "G":["D", "E", "F", "H", "J"], "H":["G", "K"], "I":["F", "J", "K"], "J":["G", "I"], "K":["B", "H", "I"] }

SOLUTION

Applications

Existence d'un chemin

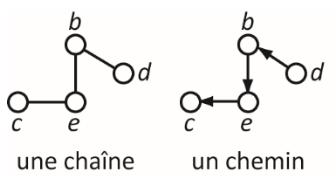
Un chemin dans un graphe orienté est une succession d'arcs qui permet d'aller d'un sommet à un autre;
Dans un graphe non-orienté, une telle succession d'arêtes est appelée une chaîne.

Mais pour simplifier nous utiliserons le terme "chemin" aussi bien dans le cas des graphes orientés ou non; et plus précisément, nous chercherons des chemins élémentaires, c'est à dire qui ne passent pas deux fois par le même sommet.

Principe

Comment déterminer si il existe un chemin élémentaire entre deux sommets, et surtout, quel est alors ce chemin ? Voila un problème qui se rencontre par exemple dans la recherche de la sortie d'un labyrinthe ( ce sera traité en application.), ou alors savoir si un routeur donné dans un réseau est accessible de tous les autres.

Le parcours en profondeur permet de trouver un chemin entre deux sommets ( dont l'un constitue la racine du parcours ) : en effet, il suit les sommets de voisins en voisins, et "revient en arrière" si il aboutit à une impasse pour "repartir" d'un nouvel embranchement ( c'est pourquoi on parle parfois de bactracking ou retour en arrière pour cet algorithme ).

Attention, l'algorithme permet simplement de savoir si un chemin existe entre deux sommets, ce n'est pas forcément le plus court !

Le problème est que le parcours du graphe ne garde pas la trace des sommets sur le chemin à suivre : le parcours explore tous les sommets du graphe, mais on ne voudrait "garder" que ceux "que l'on ne visite qu'une seule fois"...

Pour cela, il va donc falloir, pour chaque sommet visité, stocker ( par exemple dans un dictionnaire, initialisé comme vide ) le prédécesseur dans le parcours du graphe de ce sommet, c'est à dire le "sommet ( unique) d'où l'on vient" pour chaque sommet visité; ce dictionnaire aura même deux rôles :

on pourra, en "remontant" la liste des prédécesseurs jusqu'au début du parcours, "reconstituer" le chemin à suivre.
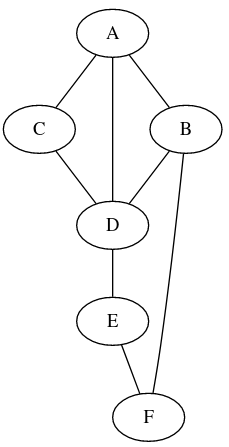
Par exemple, dans le graphe ci-contre, le dictionnaire des prédécesseurs associé à un parcours en profondeur depuis le sommet 'A' est :
```
pred = {'A': None, 'B': 'A', 'C': 'A', 'D': 'A', 'E': 'D', 'F': 'E'}				
						
```
A partir de ce dictionnaire, on peut alors "reconstruire" n'importe quel chemin depuis le sommet 'A', en partant du sommet de fin puis en remplaçant progressivement un sommet par son prédécesseur.
Par exemple, pour le chemin de 'A' à 'F' :
```
'A' -> 'D' -> 'E' -> 'F'				
						
```
( non, ce n'est pas le plus court chemin...)
Ce dictionnaire remplacera également la structure mémorisant les sommets déjà visités ( le tableau visites des implémentations de parcours précédentes ) : un sommet qui n'est pas dans le dictionnaire n'a donc pas encore été visité...

Dans ce dictionnaire, le sommet de départ du parcours aura bien entendu None comme prédécesseur.

Utilisation du parcours en profondeur pour trouver un chemin

Écrire une fonction cherche_chemin qui renvoie le dictionnaire des prédécesseurs pour un parcours entre deux sommets quelconques depart et fin d'un graphe si un chemin existe effectivement.

Penser que l'on n'a pas besoin de parcourir tous les sommets du graphe : dès que l'on rencontre le sommet de fin, on peut arrêter la recherche;
et bien sûr, si l'on a terminé le parcours et que l'on n'a pas trouvé le sommet de fin, c'est donc que le chemin n'existe pas...

#from pile import * #from collections import deque def cherche_chemin(G, depart, fin)->dict: """ Renvoie le dictionnaire des prédécesseurs pour un parcours en profondeur d'un graphe entre deux de ses sommets, si le chemin entre ces sommets existe. Entrées : G = le graphe depart = sommet de départ fin = sommet d'arrivée Sortie : le dictionnaire des prédécesseurs des sommets si le chemin existe une information ( None par exemple ) indiquant que le chemin n'existe pas dans le cas contraire """ pass # Graphe de l'exemple en introduction : g = { "A": ["B", "C"], "B": ["D", "F"], "C": ["D"], "D": ["E"], "E": ["F"], "F": [] }

SOLUTION

Une fonction pour reconstruire un chemin

On suppose maintenant disposer du dictionnaire des prédécesseurs complet ( donc, à la fin du parcours ); le chemin sera alors déterminé à partir de ce dictionnaire à l'aide d'une fonction annexe chemin.

Le chemin sera renvoyé sous la forme d'une liste des sommets à suivre depuis le départ jusqu'à la fin du chemin : ['A', 'D', 'E', 'F']

Écrire cette fonction, et la tester avec un dictionnaire simple.

Cette fonction peut être codée très simplement sous forme récursive ! Comme d'habitude, réfléchir à son cas de base et à son cas général...

def chemin(fin, pred: dict)->list: '''Fonction qui reconstruit le chemin depuis un sommet de départ jusqu'à un sommet de fin en utilisant le dictionnaire des prédécesseurs de chaque sommet dans le parcours depuis le sommet de départ. Entrées : fin = le sommet à atteindre pred = le dictionnaire associant à chaque sommet l'étiquette de son prédécesseur dans le parcours du graphe depuis le sommet de départ Sortie : le tableau ( dans l'ordre ) des sommets à suivre depuis la racine du parcours jusqu'au sommet 'fin' ''' pass # Dictionnaire pour l'exemple de ce paragraphe : pred = {'A': None, 'B': 'A', 'C': 'A', 'D': 'A', 'E': 'D', 'F': 'E'}

SOLUTION

Recherche et affichage

Utiliser maintenant les deux fonctions conjointement pour vérifier que la recherche du chemin est effective dans le graphe de l'exemple de ce paragraphe.
Utiliser également ces fonctions pour montrer qu'un chemin existe dans le deuxième graphe entre les sommets 'A' et 'F', mais pas entre 'A' et 'E'.

#from pile import * #from collections import deque def cherche_chemin(G, depart, fin)->dict: pass def chemin(fin, pred: dict)->list: pass # Graphe de l'exemple en introduction : g = { "A": ["B", "C"], "B": ["D", "F"], "C": ["D"], "D": ["E"], "E": ["F"], "F": [] } # Deuxième graphe : g2 = { "A": ["B", "C"], "B": ["D", "F"], "C": ["D"], "D": ["E"], "E": [], "F": ["E"] }

Plus court chemin entre deux sommets

Voila un autre problème, mais vous allez voir que ce n'est pas beaucoup plus compliqué...

Vous imaginez bien : cette fois-ci, c'est le parcours en largeur qui va permettre de résoudre ce problème.

En effet, le parcours en largeur parcourt les sommets du graphe en "s'éloignant" progressivement de la racine du parcours; lorsqu'on rencontre le sommet d'arrivée, on est donc assurés d'avoir parcouru le plus petit nombre d'arêtes/arcs.

On doit cependant là aussi garder la trace des sommets à parcourir, c'est pourquoi le stockage des prédécesseurs de chaque sommet dans le parcours sera également nécessaire.

Écrire une fonction plus_court_chemin de façon à ce qu'elle renvoie le plus court chemin entre deux sommets quelconques, en utilisant également la fonction annexe de reconstruction du chemin.

L'algorithme trouve-t-il cette fois bien le plus court chemin ?

#from file import * #from collections import deque def chemin(fin, pred)->str: pass def plus_court_chemin(G, depart, fin)->dict: '''Fonction qui renvoie le dictionnaire des prédécesseurs pour un parcours d'un graphe en largeur entre deux de ses sommets, si le (plus court) chemin entre ces sommets existe. Entrées : G = le graphe depart = sommet de départ fin = sommet d'arrivée Sortie : le dictionnaire des prédécesseurs des sommets si le chemin existe une information indiquant que le chemin n'existe pas dans le cas contraire ''' pass

SOLUTION

recherche d'un chemin → parcours en profondeur
recherche du plus court chemin → parcours en largeur

Pourquoi ne pas toujours utiliser le parcours en largeur pour trouver un chemin dans un graphe, puisque celui-ci nous donne en plus le plus court des chemins ( si il existe bien entendu ) ?

Il faut voir que le parcours en largeur parcours tous les sommets du graphe en "s'éloignant" progressivement du sommet de départ; dans un très grand graphe, il peut se passer un moment avant que l'on ne "tombe" sur le sommet d'arrivée si celui-ci se trouve très éloigné du départ.

Le parcours en profondeur "explore" au contraire un chemin en suivant toutes les possibilités jusqu'à aboutir à une "impasse", auquel cas il "retourne en arrière" pour "explorer une nouvelle piste"; il y a donc beaucoup plus de chances que l'on tombe ainsi plus rapidement sur le sommet d'arrivée, dans la mesure bien sûr où le chemin existe...

Il existe des algorithmes de recherche de plus court chemin plus efficaces que BFS, mais si la seule recherche de l'existence d'un chemin suffit, alors DFS peut suffire...

Détermination de la présence d'un cycle/d'un circuit

Un graphe non orienté présente un cycle si il existe une suite d'arêtes, une chaîne, dont le sommet de début et de fin est le même.
Dans le cas d'un graphe orienté, une telle suite d'arcs est appelée un circuit.

La recherche de la présence d'un cycle dans un graphe permet de détecter, par exemple, des situations où des informations tourneraient "en boucle" dans un réseau, et optimiser celui-ci, ou alors transformer le graphe en arbre ( qui est, on le rappelle, un graphe orienté acyclique ).

Le principe est simple : il faut chercher si il existe dans le graphe un chemin entre le sommet de départ...et lui-même !
Dans la pratique, à partir d'un de ses sommets, on parcourt le graphe ( en largeur ou en profondeur, peu importe..), et si en un point du parcours, on "retombe" sur le sommet de départ ( graphe orienté ) ou un sommet déjà visité ( graphe non-orienté ), alors le graphe comporte effectivement un cycle.

Cependant, dans un graphe orienté, ou non-orienté mais pas ( complètement ) connexe, il peut y avoir des sommets "non-accessibles" selon le sommet duquel on commence le parcours, et la recherche d'éventuels cycles ne sera donc pas exhaustive : il faut donc recommencer le parcours depuis tous les sommets ( dans l'idéal, il faudrait en fait faire le parcours de toutes les composantes connexes du graphe, mais la détermination de celles-ci n'est pas au programme. Alors, tant pis pour le O(n²) 😌...).

Circuit dans un graphe orienté

Dans ce cas, l'algorithme est très simple : c'est une simple adaptation de la recherche d'un chemin entre deux sommets; à chaque "découverte" d'un nouveau sommet, on teste simplement si il a déjà été visité : si c'est le cas, et si ce sommet est celui de départ, alors on a détecté un circuit ; dans le cas contraire, on continue le parcours :


pour chaque sommet v adjacents du sommet courant
    si v n'a pas encore été visité:
        marquer le sommet v comme visité
        continuer le parcours à partir de v
    sinon, si on est revenu au sommet de départ:
        on a détecté un circuit !

Il serait également intéressant d'afficher le circuit au cas où celui-ci est détecté.

Pour cela, on peut lors de la recherche de circuit, remplir un dictionnaire des prédécesseurs comme cela a été fait dans la recherche de chemin.
Combiné à la fonction de "reconstruction" d'un chemin, ceci permettra d'identifier le circuit détecté dans le graphe.

écrire une fonction cherche_circuit, qui :
- prend comme paramètre un graphe et le sommet de départ
- renvoie le dictionnaire des prédécesseurs de chaque sommet si un circuit est détecté, None sinon.
Attention, il faudra que ce dictionnaire représente complètement le chemin d'un sommet....vers lui-même !! Par exemple, pour le graphe circuit, on doit obtenir :
```
pred = {'B': 'E', 'K': 'B', 'H': 'K', 'I': 'K', 'F': 'I', 'G': 'F', 'E': 'G', 'J': 'G'}					
					
```
En adaptant la fonction de "reconstruction" d'un chemin à partir du dictionnaire des prédécesseurs, écrire une fonction affiche_circuit qui renvoie le tableau des sommets représentant un circuit.
Utiliser les 3 fonctions avec les 2 graphes cycliques donnés en exemple pour vérifier le bon fonctionnement de votre implémentation.

def cherche_circuit(G, s)->dict: """ Parcourt un graphe depuis un de ses sommets afin de détecter un éventuel circuit. Entrées : G = le graphe ( orienté ) s = le sommet de départ du parcours Sortie : le dictionnaire des prédécesseurs de chaque sommet si un circuit est détecté, None sinon. """ pass def affiche_circuit(u, depart, pred:dict)->list: """ Renvoie un circuit sous la forme d'un tableau de sommets. Entrées : u = le sommet courant depart = le sommet de départ du circuit pred = le dictionnaire des prédécesseurs dans le circuit Sortie : tableau des sommets représentant le circuit """ pass def contient_circuit(G)->list: """ Recherche un circuit à partir de chacun des sommets du graphe, et l'affiche le cas échéant. """ for s in G.liste_sommets(): res = cherche_circuit_v2(G, s) if res is not None: return affiche_circuit(s, s, res) # reconstruction du circuit depuis le sommet...jusqu'à lui-même return None pas_circuit = {"A":["C"], "B":["K"], "C":[], "D":["C", "E", "G"], "E":["B"], "F":[], "G":["E", "F", "H", "J"], "H":[], "I":["F"], "J":["I"], "K":["H", "I"] } circuit = {"A":["C"], "B":["K"], "C":[], "D":["C", "E", "G"], "E":["B"], "F":["G"], "G":["E", "H", "J"], "H":[], "I":["F"], "J":["I"], "K":["H", "I"] }

SOLUTION

Cycle dans un graphe non-orienté

Dans ce cas, l'approche est un peu différente : on détecte un cycle si, au cours du parcours, on rencontre simplement un sommet déjà visité.

Mais il y a une contrainte : dans un graphe non orienté, un sommet déjà visité peut être le prédécesseur direct du sommet en cours de visité; le prédécesseur est alors aussi un successeur du sommet courant , on détecterait alors faussement un cycle...

L'idée est, à toute étape de l'algorithme, de justement "garder la trace" du prédécesseur de chaque sommet en cours de visite, pour ne pas le tester comme départ d'un éventuel cycle.
Si en un point de l'algorithme, on rencontre un sommet déjà visité, mais qui n'est pas le prédécesseur du sommet courant, alors on aura détecté un cycle :

Pour cela, on pourra par exemple enfiler/dépiler un tuple constitué du sommet et de son prédécesseur


tant que la file/la pile n'est pas vide:
    defiler/dépiler (u, pred)
    marquer le sommet u comme visité
    pour tous les sommets v adjacents de u:
        si v n'a pas encore été visité:
            empiler/enfiler (v, u)
        sinon ( ⇔ v a déjà été visité ), si v n'est pas le prédécesseur de u:
            renvoyer le cycle !
on n'a pas trouvé de cycle : renvoyer None

Au début du parcours, on enfilera/empilera None comme prédécesseur du sommet de départ.

écrire une fonction cherche_cycle, qui :
- prend comme paramètre un graphe non orienté et un sommet de départ
- renvoie le dictionnaire des prédécesseurs de chaque sommet si un cycle est détecté, None sinon.
Utiliser alors la fonction contient_cycle, qui prend un graphe en paramètre, recherche la présence d'un cycle, et affiche le cycle au cas où celui-ci existe dans le graphe
Cette fonction utilisera une fonction affiche_cycle adaptée de la fonction affiche_circuit.

def cherche_cycle(G, s)->dict: """ Parcourt un graphe depuis un de ses sommets afin de détecter un éventuel cycle. Entrées : G = le graphe s = le sommet le sommet de départ Sortie : le dictionnaire des prédécesseurs de chaque sommet si un cycle est détecté, None sinon. """ pass def affiche_cycle(u, depart, pred:dict)->str: """ Renvoie un cycle sous la forme d'un tableau de sommets Entrées : u = le sommet courant depart = le sommet de départ du cycle pred = le dictionnaire des prédécesseurs dans le cycle Sortie : tableau des sommets représentant le cycle """ pass def contient_cycle(G)->str: """ Recherche un cycle à partir de chacun des sommets d'un graphe non-orienté, et l'affiche le cas échéant. """ for s in G.liste_sommets(): res = cherche_cycle(G, s) if res is not None: return affiche_cycle(s, s, res) # reconstruction du circuit depuis le sommet...jusqu'à lui-même return None pas_cycle = {"A":["C"], "B":["C"], "C":["A","B","D","E"], "D":["C", "F"], "E":["C","G"], "F":["D"], "G":["E", "H", "I"], "H":["G"], "I":["G"] } cycle = {"A":["C"], "B":["C"], "C":["A","B","D","E"], "D":["C", "F"], "E":["C","G"], "F":["D","G"], "G":["E", "F", "H", "I"], "H":["G"], "I":["G"] }

Distances entre deux sommets

Algorithmes pas au programme officiel. Ce sont des "prolongements" de l'algorithme du parcours en largeur.

Plus petite distance en nombre d'arcs/d’arêtes

La plus petite distance entre deux sommets d’un graphe est la longueur du plus petit chemin possible entre ces deux sommets. Dans un graphe non pondéré, elle est donc égale au nombre minimal d'arêtes/d'arcs à parcourir entre les deux sommets.

Dans le parcours en largeur, on "s'éloigne" petit à petit de la racine du parcours. En tenant le compte du nombre de "niveaux" dont l'algorithme s'est "éloigné" depuis la racine, il permet donc de déterminer la distance entre la racine du parcours et chaque sommet du graphe.

Ceci est une simplification de l'algorithme plus général appelé algorithme de Dijkstra, qui calcule les distances d'un sommet donné à tous les autres dans un graphe pondéré.

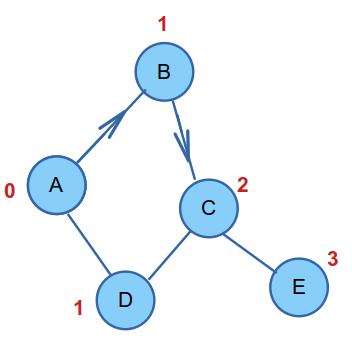
Distances dans un graphe — Distances des sommets depuis le sommet A

Le dictionnaire des prédécesseurs n'est plus nécessaire puisqu'on ne s’intéresse pas ici à un chemin en particulier. A la place, on stockera les distances de chaque sommet depuis le sommet de départ du parcours.

Le principe : on réalise donc un parcours BFS du graphe depuis un sommet de départ.
Pour chaque sommet pas encore visité, on calcule sa distance depuis le sommet de départ : on alors a parcouru une arête/un arc de plus depuis le prédécesseur du sommet; la distance de ce sommet à la racine du parcours est donc celle de son prédécesseur augmentée de 1.

a quel moment de l'algorithme change-t-on de "niveau d'exploration" en passant au niveau "suivant" ?
que faut-il alors modifier dans l'algorithme BFS pour calculer la distance de chaque sommet en cours de visite depuis le sommet de départ du parcours ?
écrire alors une fonction distances qui calcule les distances de chaque sommet du graphe à un sommet de départ du parcours.
tester la fonction sur un graphe non orienté.

#from file import * #from collections import deque def distances(G, depart)->dict: '''Fonction qui calcule les distances depuis un sommet du graphe à tous les autres sommets. Entrée : G = le graphe depart = le sommet de départ Sortie : le dictionnaire donnant pour chaque sommet sa distance depuis le sommet de départ ''' pass

SOLUTION

Plus petite distance dans un graphe pondéré

Dans ce cas, on part du principe que, par exemple, le "poids" d'un arc/d'une arête représente la distance entre deux sommets : plus le poids est grand, plus cette distance est élevée.

La situation est plus délicate à traiter : en effet, si il y a plusieurs chemins pour aller jusqu'à un sommet donné, leurs longueurs cumulées ne sont généralement pas les mêmes; il va alors falloir dans ce cas pouvoir déterminer laquelle est la plus petite...

Une "vraie" recherche du plus court chemin doit donc tenir compte de la distance cumulée depuis le début du parcours.

L'algorithme de Dijkstra

Pour cela, l'algorithme de Dijkstra ( hors programme ) utilise une structure de données appelée file à priorité ( FAP ) pour stocker, puis sélectionner, pour chaque sommet, l'arête/arc de plus faible "poids" dans la longueur totale du chemin à suivre d'un sommet aux autres sommets d'un graphe :

Cet algorithme est étudié en détails ailleurs dans ce cours dans le contexte du routage sur un réseau.

C'est donc un parcours en largeur d'un graphe pondéré avec recherche du plus court chemin; cet algorithme donne un résultat optimal, mais peut être très lent sur de (très) grands graphes.

Algorithme

On initialise les distances (« distances ») de tous les sommets à l’infini : on n’a aucune information les concernant
On met le sommet de départ à une distance 0 puisque l’on part de ce sommet
On n’a visité aucun sommet, donc on crée une liste de sommets visités vide
Tant qu’il y a des distances infinies dans les sommets non visités (pour être sûr de ne pas manquer le chemin le plus court) :
- On détermine le sommet le plus proche, non visité, du sommet où on est et on y voyage
- On détermine les voisins du sommet où on arrive
  - Comparaison de la distance déjà calculée des voisins avec la distance obtenue si on passe par le sommet où l’on est
  - Si la distance, en passant par le sommet où l’on est, est plus petite que la distance en mémoire, on la met à jour pour obtenir la plus petite distance possible
- On marque le sommet comme visité
On retourne la liste des distances (« distances »)

Une implémentation en Python peut être trouvée ici.

Autres algorithmes du plus court chemin

Une amélioration de l'efficacité de l'algorithme de Dijkstra est l’algorithme A* ( "A-star" ), qui utilise une heuristique pour déterminer à chaque étape, la "direction" vers laquelle aller pour atteindre le sommet d'arrivée.
Cet algorithme ne donne pas forcément un résultat optimal, mais est beaucoup plus rapide; c'est celui qui est utilisé comme IA dans de nombreux jeux.

Visualisation de différents algorithmes de recherche de plus court chemin

https://honzaap.github.io/Pathfinding/