TP Labyrinthe

Sortir du labyrinthe

On peut considérer un labyrinthe comme un ensemble de "cases" dans une grille; une case "vide" indique par exemple un passage, alors qu'une case "pleine" indique un mur :

Un labyrinthe est le plus souvent représenté sous forme d'un tableau de tableaux en mémoire , chaque case étant à l'intersection d'une ligne et d'une colonne de cette grille :


# '0' = case vide / '1' = mur )
laby = [
    [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], 
    [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1], 
    [1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1], 
    [1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1], 
    [1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1], 
    [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], 
    [1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], 
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1]
]

Attention, ce n'est pas du tout une matrice d'adjacence.

Le parcours d'un labyrinthe pour en trouver la sortie peut alors être fait en utilisant par exemple la récursivité ( avec les limites que l'on connaît pour les très grands labyrinthes ).

Pour ce projet cependant, on utilisera une approche purement "relationnelle" : le labyrinthe sera modélisé par un graphe, où les cases vides représentent les sommets du graphe, et le fait que deux cases "vides" sont reliés entre elles correspondra à l'existence d'une arête entre ces deux sommets.

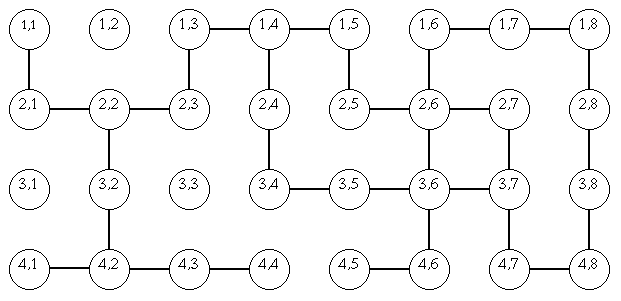
Trouver la sortie d'un labyrinthe revient donc à chercher un chemin dans le graphe entre le "sommet d'entrée" du labyrinthe et le "sommet de sortie".

Modélisation du labyrinthe

Le graphe sera implémenter sous forme de dictionnaire de listes d'adjacence.

Cependant attention, un sommet ne sera pas désigné par un simple caractère mais sera étiqueté par un tuple contenant les coordonnées (ligne, colonne) dans la grille de la case correspondant à ce sommet ( cf. image ci-dessus ).

En parcourant le tableau de tableaux passé comme argument, on devra créer les sommets du graphe mais également les relations qui existent entre deux cases lorsque celles-ci communiquent ( c'est à dire que les sommets sont adjacents ).
Ces relations devront a priori être à double sens ( graphe non orienté ).

Pour créer le graphe, vous pouvez vous inspirer de l'algorithme optimisé suivant :

On parcourt la grille case par case, de gauche à droite et de haut en bas;
si la case courante contient 0, on crée le sommet correspondant à cette case,
si la case à gauche de la case courante contient aussi un 0, on crée une arête entre les deux cases,
idem pour la case juste en dessous de la case courante.

En précédant ainsi, lors de la création d'une arête, il n'y a pas besoin de tester l'existence des sommets correspondants dans le graphe, ils existent forcément !

Écrire une fonction cree_graphe qui prend comme paramètre le tableau de tableaux laby et renvoie le graphe modélisant le labyrinthe.

Pour vérifier que le graphe créé est correct, vous pourrez afficher son dictionnaire de listes d'adjacence, ou utiliser la fonction dessine_graphe du module graphe si vous l'aviez implémentée.

def cree_graphe(laby: list[list])->dict: """ Fonction qui crée le graphe modélisant un labyrinthe décrit par un tableau de tableaux. Entrée: laby = tableau de tableaux modélisant le graphe - Codage : 0 = case vide / 1 = mur Sortie : Le graphe sous forme de listes d'adjacence. Chaque sommet y est désigné par un tuple (ligne, colonne) dans le labyrinthe """ pass # '0' = case vide / '1' = mur ) laby = [ [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1] ]

SOLUTION

Trouver la sortie du labyrinthe

La question : à partir de l'entrée du labyrinthe, quel chemin suivre pour atteindre la sortie ( pas forcément le plus court...) ?

C'est un problème classique pour lequel plusieurs techniques sont possibles pour une personne se trouvant à l'intérieur du labyrinthe.

Mais nous avons la chance d'avoir le plan du labyrinthe ! Laissons alors l'ordinateur déterminer la sortie à notre place...

Écrire une fonction trouver_sortie qui prend comme paramètre le graphe modélisant le labyrinthe, le sommet d'entrée et le sommet de sortie, et qui détermine le chemin à suivre pour sortir du labyrinthe depuis le sommet d'entrée jusqu'au sommet de sortie ( qui doivent bien entendu être dans le graphe...).

La fonction renverra le chemin à suivre sous une forme à déterminer (liste des sommets à suivre par exemple ).

def trouver_sortie(g: dict, depart: tuple, arrivee: tuple)->list: """ Fonction qui détermine le chemin à suivre pour sortir d'un labyrinthe. Entrée: g = le graphe modélisant le labyrinthe depart = tuple (ligne, colonne) représentant le sommet de départ arrivee = idem pour le sommet d'arrivée Sortie : le tableau des sommets à suivre pour aller du sommet de départ à celui d'arrivée """ pass

Attention à la manière dont est représenté chaque sommet ( un tuple ) dans le graphe.

Vérifier que la fonction donne le bon résultat !! ( facile à déterminer sur le graphe en exemple...)

SOLUTION

Affichage et visualisation du chemin à suivre

La méthode imshow du module Matplotlib.pyplot permet d'afficher une matrice "2D", avec des couleurs différentes selon la valeur des éléments de la matrice : c'est tout à fait ce qu'il nous faut pour visualiser le résultat de la recherche de parcours de sortie !

Écrire une fonction affiche qui :

prend comme paramètres la matrice représentant le labyrinthe et la liste des sommets à suivre de l'entrée à la sortie du labyrinthe.
modifie la matrice ( ou sa copie...) de manière à placer la valeur 2 ( ou toute autre valeur différente de 0 ou 1 ) dans les éléments correspondants aux cases du parcours à suivre
utilise la méthode imshow pour afficher le labyrinthe et son chemin de sortie.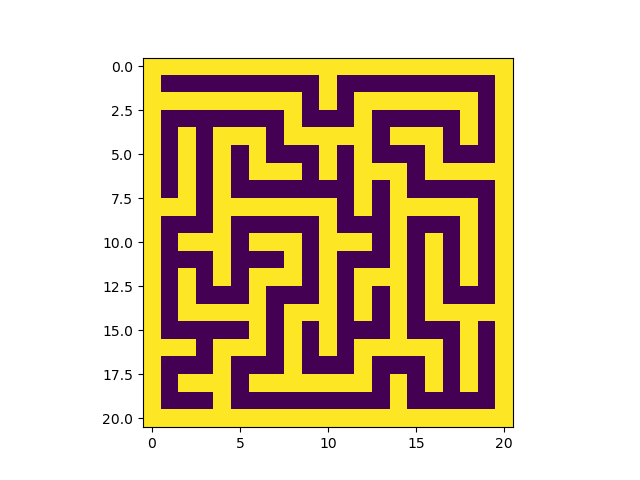

import matplotlib.pyplot as plt def affiche(laby: list[list], chemin: list)->None: """Fonction qui affiche le labyrinthe et le chemin de sortie. Entrées: laby = le tableau de tableaux représentant le labyrinthe chemin = la liste des sommets à suivre pour sortir du labyrinthe Sortie: Aucune """ pass plt.imshow(laby) plt.show()

SOLUTION

Prolongement possible

Les fichiers textes ci-dessous contiennent la description de quelques labyrinthes selon le codage suivant : 0 = case vide, 1 = mur, 4 = entrée, 5 = sortie.
Une case correspond à un caractère de chaque ligne.

laby0.txt, laby1.txt, laby2.txt

Écrire une fonction qui extrait les informations de ces fichiers pour en tirer le tableau de tableaux représentant le labyrinthe, puis utiliser les fonctions précédentes pour résoudre le labyrinthe !

SOLUTION

Créer des labyrinthes

De très nombreux algorithmes existent pour générer des tableaux de tableaux représentant un labyrinthe; en voici un qui produit des labyrinthes parfaits, c'est à dire dont chaque case est relié à une autre par un unique chemin.

Il utilise un parcours de graphe en profondeur avec retour en arrière ( backtracking ) :

on part d'un labyrinthe ne contenant que des murs
à partir d'une case donnée, l'algorithme crée aléatoirement un chemin en "cassant" des murs, tant qu'il peut trouver des cases encore non explorées
si il n'y a plus de case non explorée au bout du chemin, l'algorithme "revient en arrière" au début du chemin, et recherche un nouveau chemin à partir de là, y créant donc une "intersection" dans le labyrinthe
si toutes les cases du labyrinthe ont été explorées, l'algorithme s'arrête...

Cet algorithme suppose de garder la trace des cases déjà explorées, ainsi que celle des débuts de chemins, afin d'y revenir au besoin ("backtracking" ).

Même si l'algorithme ressemble à un parcours de graphe, il n'est pas nécessaire de créer un graphe à proprement parler : c'est le tableau de tableaux qui sera directement modifié.


fonction creer_laby(s: sommet courant):
	
	ajouter s à la liste des cases déjà explorées
   
	si il y a des cases accessibles depuis s et pas encore explorées:
		en prendre une au hasard
		casser le mur entre elle et s
		ajouter s à la liste des débuts de chemin
		appeler récursivement la fonction creer_laby à partir de la nouvelle case
	sinon:
		extraire le dernier début de chemin de la liste des débuts ( si il en reste un )
		appeler récursivement la fonction creer_laby à partir de lui

Le plus délicat est de déterminer les cases accessibles depuis une case donnée.

Écrire une fonction creer_laby qui implémente l'algorithme ci-dessus pour générer un tableau de tableaux représentant un labyrinthe, et l'afficher ensuite.

Le tableau initial ne contenant que des murs est déjà donné, pour un nombre de lignes et de colonnes modifiables.

Les murs sont en jaune, les cases vides en violet.

L'entrée et la sortie du labyrinthe sont placées et peuvent être modifiées.

Le point d'entrée de l'algorithme pourra être n'importe quelle case vide ( pas un mur évidemment ), pas forcément l'entrée ou la sortie.

from random import randint, shuffle # à utiliser au besoin import matplotlib.pyplot as plt # pour l'affichage du labyrinthe def creer_laby(laby: list[list], s: tuple[int, int], visites: list, debuts: list)->list[list]: """Fonction qui créé un tableau de tableaux représentant un labyrinthe, à l'aide de l'algorithme de parcours en profondeur avec retour en arrière. Entrées : laby = le tableau de tableaux représentant le labyrinthe, ne contenant que des murs au premier appel s = la case courante visites = la liste des cases déjà explorées débuts = la liste des débuts de chemin Sortie: le tableau de tableaux modifié """ pass # Dimensions du labyrinthe H = 10 L = 10 # labyrinthe ne contenant que des "murs": laby = [[0 if i%2!=0 and j%2!=0 else 1 for j in range(2*L+1)] for i in range(2*H+1)] # entrée et sortie du labyrinthe ( peuvent être déplacées ) laby[0][1] = 0 # entrée laby[2*H][2*L-1] = 0 # sortie debut = (0, 1) # point d'entrée de l'algorithme ( peut être modifié ) laby = creer_laby(laby, debut, [], []) plt.imshow(laby) plt.show()

SOLUTION