Parcours des arbres

Il peut être nécessaire de parcourir l'ensemble des nœuds d'un arbre (pour les répertorier, pour réaliser une recherche, pour obtenir une liste triée avec un ABR, ou tout simplement pour transmettre un arbre d'un système à un autre dans un fichier texte...), mais au vu de la structure hiérarchique, il n'y a pas de parcours classique à priori (contrairement à la liste, ou le parcours est "naturel").
Voici quelques exercices de parcours d'arbre et leur correction.

Parcours en profondeur (d'abord)..ou DFS (Deep First Search)

Beaucoup d’algorithmes se résument à traiter individuellement chaque nœud de l’arbre (pour en faire la liste, pour effectuer un calcul...). On se donne donc une opération Traiter à appliquer à chaque nœud.
Dans le parcours en profondeur, on va profiter de la structure récursive de l'arbre binaire. Parcourir un arbre c'est :

parcourir le sous arbre gauche
parcourir le sous arbre droit

Reste a savoir quand traiter le nœud commun à ces deux sous arbres...

Avant de parcourir les deux sous arbres → parcours préfixe
Entre le parcours des deux sous arbres → parcours infixe
Après le parcours des deux sous arbres → parcours suffixe

Parcours préfixe

Dans ce parcours, nous traitons donc la racine avant de parcourir ses deux sous arbres. Par exemple pour l'arbre ci-dessous:

Parcours

( cochez pour l'exemple ci-dessous )

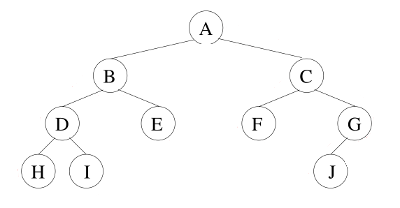
L'algorithme du parcours préfixe d'un arbre est donc le suivant :

		
parcoursPrefixe(Arbre):

Traiter la racine de l'arbre 

Si il y a un sous arbre gauche
	parcourir le sous arbre gauche

Si il y a un sous arbre droit
	parcourir le sous arbre droit

A vous de coder une fonction ( ou une méthode de la classe Arbre ) pour le parcours préfixe d'un arbre, et de la tester sur quelques exemples. Le traitement utilisé sera uniquement l'affichage de la valeur du nœud.

from classe_arbre import * def parcours_prefixe(arbre): pass arbre = Arbre('A', Arbre('B', Arbre('D', Arbre('H'), Arbre('I')), Arbre('E')), Arbre('C', Arbre('F'), Arbre('G', Arbre('J'))))

SOLUTION

Parcours infixe

Une fois que vous avez compris le parcours préfixe, les deux suivants sont très simples, il suffit de déplacer la place du traitement dans l'algorithme de parcours. Ainsi il devient :

		
parcoursInfixe(Arbre):

Si il y a un sous arbre gauche
	parcourir le sous-arbre gauche

Traiter la racine de l'arbre	

Si il y a un sous arbre gauche
	parcourir le sous-arbre droit

Parcours

( cochez pour l'exemple ci-dessous )

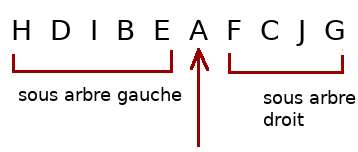
A vous de coder une fonction, ou une méthode, pour le parcours infixe d'un arbre et de la tester sur quelques exemples. Le traitement utilisé sera uniquement l'affichage de la valeur du nœud.

from classe_arbre import * def parcours_infixe(arbre): pass arbre = Arbre('A', Arbre('B', Arbre('D', Arbre('H'), Arbre('I')), Arbre('E')), Arbre('C', Arbre('F'), Arbre('G', Arbre('J'))))

SOLUTION

Parcours suffixe

Une fois que vous avez compris les deux autres parcours, le suffixe est évident. L'algorithme devient :

		
parcoursSufixe(Arbre):

Si il y a un sous arbre gauche
	parcourir le sous arbre gauche

Si il y a un sous arbre droit
	parcourir le sous arbre droit
	
Traiter la racine de l'arbre

Parcours

( cochez pour l'exemple ci-dessous )

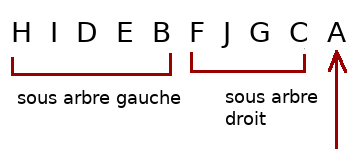
A vous de coder une fonction, ou une méthode, pour le parcours suffixe d'un arbre et de la tester sur quelques exemples. Le traitement utilisé sera uniquement l'affichage de la valeur du nœud.

from classe_arbre import * def parcours_suffixe(arbre): pass arbre = Arbre('A', Arbre('B', Arbre('D', Arbre('H'), Arbre('I')), Arbre('E')), Arbre('C', Arbre('F'), Arbre('G', Arbre('J'))))

SOLUTION

Parcours en largeur (d'abord) d'un arbre

Le parcours en largeur est assez explicite, car les nœuds sont parcourus dans la largeur de l'arbre, par "niveaux" successifs :

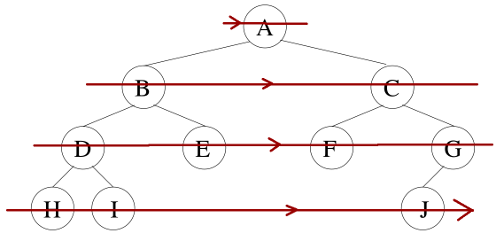
Cependant on remarque que la structure récursive de l'arbre ne pourra pas être exploitée ici.
Pour réaliser ce parcours nous auront besoin d'un TAD linéaire que vous avez déjà utilisé : la file.

L'idée est la suivante :

Enfiler la racine
La défiler puis la traiter
Enfiler ses deux nœuds fils
Défiler le premier nœud fils, le traiter
Enfiler ses deux nœuds fils
etc...

File

Parcours

( cochez pour l'exemple ci-dessus )

Si l'on écrit l'algorithme correspondant on aura :

		
parcoursLargeur(arbre):
    arbre est un arbre
    
    file est une File
    Enfiler l'arbre dans la file
    
    Tant que la file n'est pas vide
        s = défiler la file
        Traiter s
    
        Si le fils gauche de s n'est pas vide
            Enfiler le fils gauche de s dans la file
        
        Si le fils droit de s n'est pas vide
            Enfiler le fils droit de s dans la file

A vous de coder ce parcours en largeur d'un arbre et de le tester. Le traitement d'un nœud sera là-aussi l'affichage de son étiquette.
Pensez à importer au préalable un module dans lequel se trouve le code pour manipuler une structure de file; vous pouvez également utiliser la classe deque du module collections, plus efficace.

Les deques sont une généralisation des piles et des files ( deque se prononce "dèque" et est l'abréviation de l'anglais double-ended queue) : il est possible d'ajouter et retirer des éléments par les deux bouts des deques. Celles-ci gèrent des ajouts et des retraits utilisables par de multiples fils d'exécution (thread-safe) et efficients du point de vue de la mémoire des deux côtés de la deque, avec approximativement la même performance en O(1) dans les deux sens.

Il faut importer la classe deque à partir du module collections :


from collections import deque

Pour créer une deque vide :


pile = deque() # ou file = deque() bien sûr...

Il existe plusieurs méthodes pour ajouter/retirer des éléments à chaque "extrémité" d'une deque :

	A gauche	A droite
insertion d'un élément	`appendleft(x)`	`append(x)`
suppression et renvoi d'un élément	`popleft()`	`pop()`

Chaque extrémité d'une deque étant parfaitement équivalente en terme de complexité, à vous de choisir les méthodes adaptées pour la gestion de votre file ou de votre pile.

Enfin, la fonction len() peut être appliquée à une deque pour déterminer le nombre d'éléments qu'elle contient.


len(pile) # renvoie le nombre d'éléments dans la deque

from classe_arbre import * #from file import * #from collections import deque def parcours_largeur(arbre): pass # 5 feuilles : arbre = Arbre('A', Arbre('B', Arbre('D', Arbre('H'), Arbre('I')), Arbre('E')), Arbre('C', Arbre('F'), Arbre('G', Arbre('J'))))

SOLUTION

Applications

Pour les applications suivantes, si cela n'est pas spécifié, à vous de choisir le "bon" parcours d'arbre à utiliser !

Nombre de feuilles d'un arbre

Écrire une fonction nb_feuilles, qui prend un arbre en paramètre, et qui renvoie le nombre de feuilles dans cet arbre.

from classe_arbre import * #from file import File #from collections import deque def nb_feuilles(arbre)->int: pass # 5 feuilles : arbre = Arbre('A', Arbre('B', Arbre('D', Arbre('H'), Arbre('I')), Arbre('E')), Arbre('C', Arbre('F'), Arbre('G', Arbre('J'))))

SOLUTION

Feuille la plus haute

Écrire une fonction feuille_haute, qui prend un arbre en paramètre, et qui renvoie la hauteur de la feuille la plus proche de la racine.

La fonction devra utiliser un parcours en largeur d'abord de l'arbre. En cas d'ex-æquo, la fonction retournera la feuille la plus à gauche dans l'arbre.

from classe_arbre import * #from file import File #from collections import deque def feuille_haute(arbre)->int: pass # feuille la plus haute = 'E' : arbre = Arbre('A', Arbre('B', Arbre('D', Arbre('H'), Arbre('I')), Arbre('E')), Arbre('C', Arbre('F'), Arbre('G', Arbre('J'))))

SOLUTION

Tri avec un ABR

Les arbres binaires de recherche sont des structures ordonnées complexes. Nous avons constaté que pour la recherche d'un élément qu'un ABR était équivalent à une liste triée.
L'intérêt de l'ABR étant la facilité d'insertion d'un élément.
Cette structure ordonnée peut nous permettre de trier un tableau.

Attention, lisez bien l'intégralité de ce paragraphe avant de vous lancer dans le codage !

Vous devez créer une fonction tri_ABR() prenant en paramètre un tableau non trié et renvoyant un tableau trié.
Vous devrez utiliser les classes Arbre ( du module classe_arbre ), ABR avec sa méthode inserer( classe que vous aurez sans doute intérêt à mettre aussi dans son propre module à importer par souci de clarté du code ) et une fonction de parcours d'arbre.
La fonction devra donc :

Créer un ABR à partir de la liste passée en argument
Parcourir cet arbre de façon judicieuse pour créer une liste triée.

Mais, avant de vous lancer tête la première dans le code, vous devez :

Lire ce paragraphe sur les tests unitaires
Proposer trois tests unitaires dans la docstring de votre fonction

Et seulement ENSUITE, vous commencerez à coder votre fonction.
Lors de la phase de test vous utiliserez bien sur le module doctest.

from classe_arbre import * import doctest class ABR(Arbre): def inserer (self, v): if self.valeur is None: return ABR(v, None, None) elif (v < self.valeur): if self.filsgauche is None: return ABR(self.valeur, ABR(v, None, None), self.filsdroit) else: return ABR(self.valeur, self.filsgauche.inserer(v), self.filsdroit) elif (v > self.valeur): if self.filsdroit is None: return ABR(self.valeur, self.filsgauche, ABR(v, None, None)) else: return ABR(self.valeur, self.filsgauche,self.filsdroit.inserer(v)) def tri_ABR(tab: list)->list: """ Utilise un ABR pour trier un tableau. TESTS : >>> .... >>> .... """ pass

Pour finir... un peu de complexité :

Rappeler la complexité minimum d'un tri : Quelle est la complexité de la construction de votre ABR ? Quelle est la complexité de la construction de votre liste triée ? En déduire la complexité de votre fonction. Cette méthode de tri est-elle efficace ?

SOLUTION

Cet arbre est-il un ABR ?

Écrire une fonction est_abr qui prend comme paramètre un arbre, et renvoie True ou False selon que cet arbre est un ABR ou pas.

Une petite aide :

Cas général : un arbre est un ABR si cet arbre est un ABR, ET que son fils gauche est aussi un ABR, ET que son fils droit est aussi un ABR.
Cas de base : une feuille est (forcément...) un ABR 😎

Tester la fonction avec les deux arbres donnés en exemple, puis avec un ABR quelconque.

from classe_arbre import * def est_abr(arbre)->bool: pass pas_abr = Arbre(1, Arbre(3, Arbre(4, Arbre(6), Arbre(8))), Arbre(9, Arbre(2), Arbre(5))) abr = Arbre(23, Arbre(12, Arbre(6), Arbre(13)), Arbre(36, Arbre(28), Arbre(45)))

SOLUTION

"Profondeur" dans un arbre

On cherche à écrire une fonction qui détermine à quelle "profondeur" se trouve une valeur dans un arbre, c'est à dire à quel "niveau" de l'arbre cette valeur se situe : le niveau de la racine étant égal à 0, le niveau d'une valeur est donc le nombre d'arête(s) qui la sépare de la racine.

Une application pourrait être la détermination du nombre de générations d'écart entre un individu et un de ses ancêtres.

Écrire une fonction profondeur_valeur, qui prend comme paramètre un arbre et une valeur, et qui renvoie le niveau à laquelle cette valeur se situe dans l'arbre.
La fonction devra renvoyer -1 si la valeur ne se trouve pas dans l'arbre.

Une petite aide : on pourra s'inspirer de la méthode utilisée pour calculer la hauteur d'un arbre...sauf qu'ici, il faudra arrêter le calcul récursif avant d'arriver "tout en bas" de l'arbre, c'est à dire lorsqu'on a trouvé la valeur dans l'arbre; comment faire ? Et comment gérer le cas où la valeur n'est pas dans l'arbre ?

Tester la fonction avec un arbre quelconque, et avec un ABR.

from classe_arbre import * def profondeur_valeur(arbre, valeur: int, niveau = 0)->int: pass

SOLUTION

Arbres arithmétiques

Nous avons vu précédemment comment calculer une expression stockée dans un arbre arithmétique.
Mais comment obtenir cet arbre arithmétique ?

Vous devez coder une fonction encode_arbreArith(), qui prend en paramètre une chaîne de caractères contenant une expression arithmétique correcte, et qui la stocke dans un arbre arithmétique.
Nous avons déjà vu comment décoder un arbre arithmétique, mais les parcours d'arbre que nous venons de voir ne seraient-ils pas aussi une solution à ce problème ? A vous de trouver le parcours qui pourra résoudre le problème, et écrire une fonction decode_arbreArith qui utilise un parcours d'arbre arithmétique pour évaluer une expression préalablement codée.

from classe_arbre import * def encode_arbreArith(expr: str)->Arbre: pass def decode_arbreArith(arbre: Arbre)->int: pass

SOLUTION