NSI Terminale
NSI Terminale
Vous avez déjà, pendant votre scolarité, vu ou utilisé des données structurées dans des arbres :
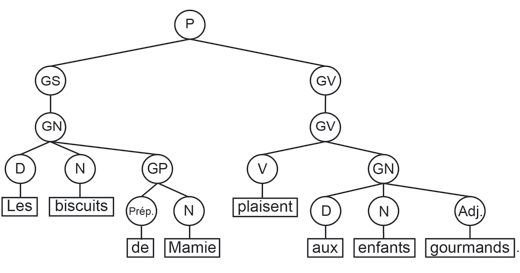
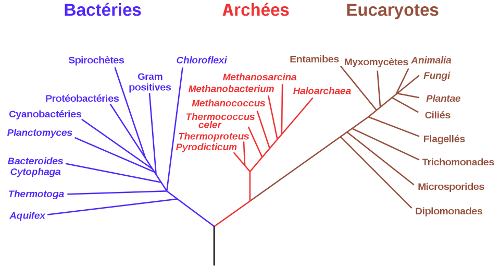
Vous en avez peut-être même déjà croisés sans le savoir au fil de vos lectures...
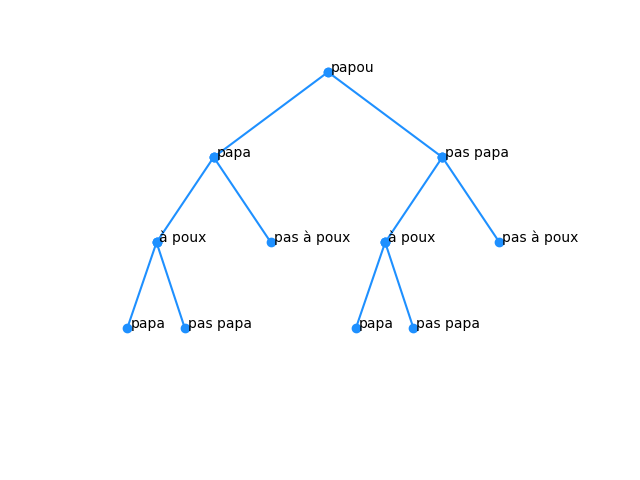
La structure d'arbre permet d'organiser des données de façon hiérarchique, ce qui simplifie ensuite la lecture et le traitement de ces données.
Il n'est pas facile de définir un arbre, car c'est en fait un cas particulier de graphe.
Nous retiendrons que dans un arbre il n'y a jamais de chemin d'un nœud vers lui même. Il n'y a jamais de cycle dans un arbre.
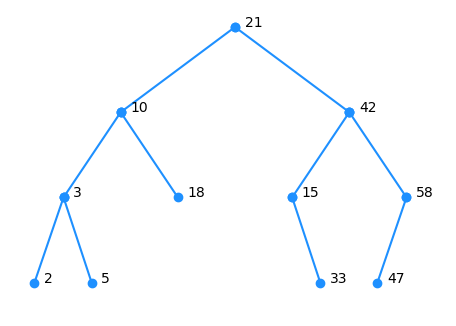
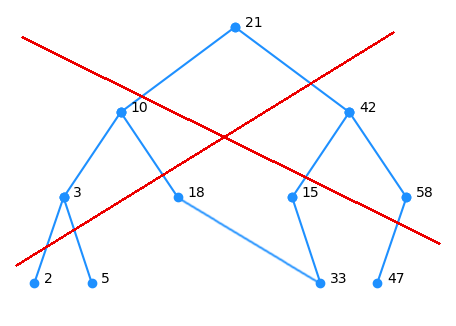
D'après vous ce qui est représenté ci-dessous est-il un arbre ?
et si c'est le cas, que semble-t-il lui manquer ?
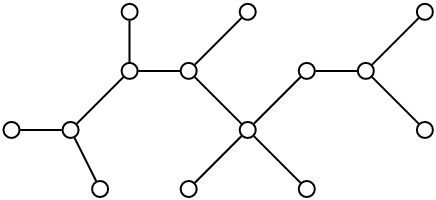
Les arbres sont très utilisés en informatique parce qu'ils permettent de stocker des données volumineuses et de rendre efficace l'accès à ces données. Voici deux exemples d'applications :
Les arbres lexicographiques sont à la base des algorithmes de compression de données. Les préfixes communs à plusieurs mots n'apparaissent qu'une seule fois dans l’arbre.
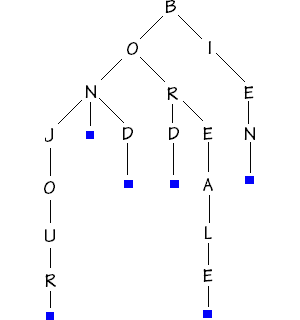
Recopiez cet arbre et ajoutez les mots "bordure" et "binaire".
Les arbres sont également utilisés en analyse syntaxique. vous avez déjà vu ce genre de choses avec les piles (vérification du parenthésage).
Voici l'arbre arithmétique qui représente l'expression (x + 1)(3y + 2) :
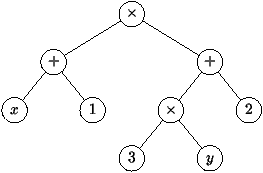
A vous de représenter l'arbre correspondant à l'expression : 3 + (x/2 + 1).
Mais on retrouve les arbres dans de multiples applications en informatique :
Comme pour tout nouveau domaine de l'informatique, il va falloir se mettre d'accord sur une série de termes nécessaire pour décrire les arbres.
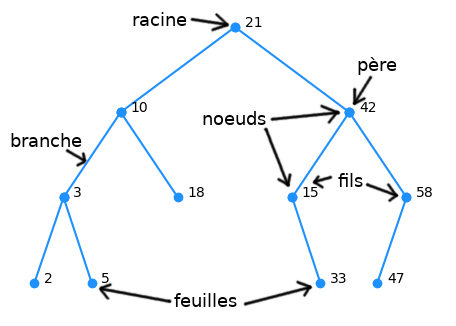
Un arbre est un ensemble organisé de nœuds. Chaque nœud a un père, sauf le nœud appelé racine.
Un nœud peut avoir un certain nombre de fils ( ou enfants ). Si un nœud n'a aucun fils, on dit que c'est une feuille.
Les nœuds sont reliés entre eux par des branches ( appelées quelquefois arêtes, ce qui est la terminologie utilisée pour les graphes ).
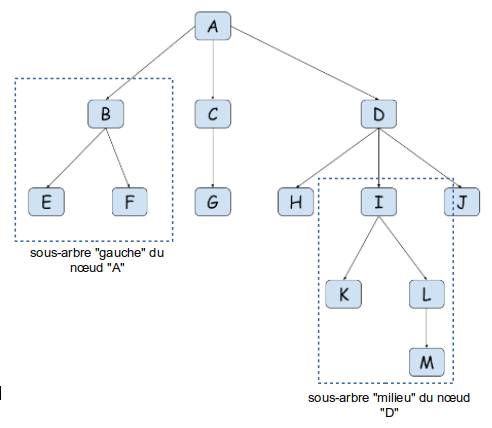
On appelle sous-arbre l'ensemble des nœuds "descendants" d'un nœud donné ( donc pas seulement le nœud-fils ) :
Chaque nœud d'un arbre peut porter ou non une étiquette. Cette étiquette peut être un entier, un texte, ou quelque chose de beaucoup plus complexe...
Dans l'arbre ci-contre, seules les feuilles ont des étiquettes.
La hauteur d'un nœud est égal au nombre de branches qu'il faut parcourir pour aller jusqu'à ce nœud depuis la racine.
La hauteur d'un arbre est la hauteur de son nœud le plus haut.
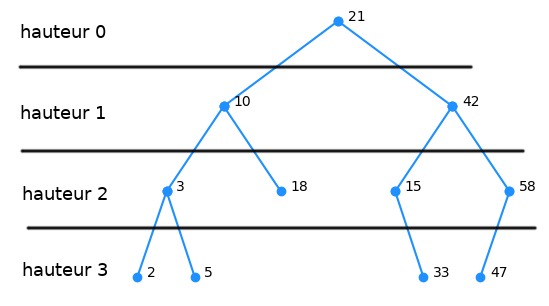
Dans certains ouvrages, la hauteur de la racine d'un arbre est considérée comme étant 1. Dans le cas précédent, la hauteur de l'arbre serait 4.
La taille d'un arbre est égale au nombre de nœuds de l'arbre.
Quelle est la taille de l'arbre ci-contre ?
Le degré d'un nœud est le nombre de fils de ce nœud.
Le degré d'un arbre est le plus grand degré de ses nœuds.
Quel est Le degré de l'arbre ci-contre ?