Arbres binaires de recherche (ABR ou BST)

Introduction

Nous avons vu que dans certains cas les arbres binaires étaient une bonne structure de données car ils permettaient de diminuer le temps d'accès à ces données.
Mais la structure d'arbre binaire est trop générale pour pouvoir s'appliquer dans de nombreux cas. Nous allons donc ajouter des contraintes à cette structure.

Structure d'un ABR

Un Arbre Binaire de Recherche (ABR ou BST en anglais) est un arbre binaire pour lequel :

Chaque nœud possède une étiquette
Il est possible de classer les étiquettes (ordre alphabétique, plus petit/plus grand ...)

de plus pour tout nœud de l'arbre :

Tous les fils du sous arbre gauche possèdent une étiquette inférieure à celle du nœud considéré
Tous les fils du sous arbre droit possèdent une étiquette supérieure à celle du nœud considéré

Parmi les 4 arbres ci-dessous, lequel est un ABR ?

SOLUTION

Les ABR ont donc par nature une structure doublement récursive :

D'une part ce sont des arbres binaires (un arbre, c'est un nœud, relié à un arbre gauche et à un arbre droit)
D'autre part, la contrainte imposée par les ABR est elle même récursive.

Construire un ABR

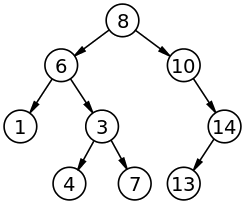
L'efficacité lors de la recherche dans un ABR dépend de la structure de cet arbre, et on peut constater ci-dessous qu'il n'existe pas un unique ABR pour un ensemble de données.

En effet les deux arbres ci-dessus sont des ABR contenant les données 1,3,4,6,7,8,10,13,14, cependant ils n'ont pas la même structure !.

Nous allons créer une nouvelle sous classe de la classe Arbre : la classe ABR :


class ABR(Arbre):

Comme au chapitre précédent, la classe ABR va hériter de la classe Arbre. Un ABR sera donc un Arbre avec des méthodes supplémentaires.

La méthode la plus importante est celle qui permet de construire un ABR à partir d'une série de données.

La méthode ci-dessous permet d'insérer une étiquette v dans un arbre (self), en respectant les contraintes des ABR. Pour bien comprendre l'algorithme mis en œuvre, répondez aux questions ci-dessous :


def inserer (self,v):
	if self.valeur==None:
		return ABR(v,None,None)

	elif(v<self.valeur):
		if self.filsgauche==None:
			return ABR(self.valeur,ABR(v,None,None),self.filsdroit)
		else:
			return ABR(self.valeur,self.filsgauche.inserer(v),self.filsdroit)

	elif (v>self.valeur):
		if self.filsdroit==None:
			return ABR(self.valeur,self.filsgauche,ABR(v,None,None))
		else:
			return ABR(self.valeur,self.filsgauche,self.filsdroit.inserer(v))

Cette méthode est-elle récursive ? Précisez les lignes qui permettent de répondre.
Quelles sont les préconditions sur cette méthode ?
Que se passe-t-il si la valeur à insérer est déjà présente dans l'ABR ?
Quelles sont les postconditions sur cette méthode ?

SOLUTION

Maintenant que vous comprenez le fonctionnement de cette méthode, nous allons tenter de construire un ABR dans un cas simple.

Vous allez devoir construire un ABR contenant les 10 premiers entiers. Pour cela, on va utiliser une liste contenant ces entiers.
Affichez à chaque fois l'ABR construit. Pour simplifier les questions, suivez la numérotation ci-dessous :

On remarquera que la méthode inserer renvoie un nouvel arbre; il faudra en tenir compte pour modifier un arbre existant après lui avoir inséré un ( ou plusieurs ) noeud(s)...

from classe_arbre import * class ABR(Arbre): def inserer (self, v): if self.valeur == None: return ABR(v, None, None) elif v < self.valeur: if self.filsgauche == None: return ABR(self.valeur, ABR(v, None, None), self.filsdroit) else: return ABR(self.valeur, self.filsgauche.inserer(v), self.filsdroit) elif v > self.valeur: if self.filsdroit == None: return ABR(self.valeur, self.filsgauche, ABR(v, None, None)) else: return ABR(self.valeur, self.filsgauche, self.filsdroit.inserer(v)) # construire un premier ABR : ABR1 avec cette liste : liste1 = [1, 2, 3, 4, 5, 6, 7, 8, 9] # construire le deuxieme ABR : ABR2 avec cette liste : liste2 = [5, 2, 1, 3, 4, 8, 7, 6, 9]

Puis répondez aux questions suivantes :

A quelle structure que vous avez déjà vue correspond l'ABR1 ?
De façon générale, quelle est la complexité de la recherche dans un tel ABR contenant n nœuds ?
Comment peut-on qualifier la structure de l'ABR2 ?
Quel choix initial sur la racine de l'ABR permet d'obtenir cette structure ?

SOLUTION

Recherche dans un ABR

Une fois la structure de l'ABR construite, l'intérêt est maintenant de l'exploiter pour retrouver un élément.
Nous allons donc enrichir la classe ABR avec une méthode recherche.
Pour une fois vous allez coder les tests AVANT de coder la fonction de recherche. Pour cela il faut bien sur connaître sa spécification et utiliser un ABR spécifique :


recherche (ABR, v):
	ABR : un arbre binaire de recherche
	v: la valeur à chercher dans l'arbre
	Renvoie Vrai si v est présente dans ABR, Faux sinon

Fonction de test

Vous devez coder une fonction test_recherche sans aucun paramètre, qui affichera si tous les tests sont vérifiés.

Votre fonction devra tester les cas suivants :

Si la valeur cherchée n'est pas présente
Si la valeur cherchée est un nœud interne
Si la valeur cherchée est la racine
Si la valeur cherchée est une feuille

...et afficher un message approprié en cas d'échec ou de réussite à ces tests.

Bien sur il n'est pas possible de tester votre fonction de test...

def test_recherche(): pass

SOLUTION

Fonction de recherche

Vous allez maintenant devoir coder une méthode de recherche dans un ABR.
Du fait de sa structure récursive, la fonction peut l'être ... Mais pas nécessairement...
Voici les deux algorithmes correspondant aux version récursives et impératives de cette méthode. A vous de coder l'une de ces deux méthodes (ou les deux si vous avez le temps...).


recherche itérative :
	ABR : un arbre binaire de recherche
	v: la valeur à chercher dans l'arbre
	Renvoie Vrai si v est présente dans ABR, Faux sinon
	
	Tant que ABR n'est pas vide et que v est différente de la racine de ABR	
		Si v<la racine de ABR
			ABR=fils gauche de ABR
		Sinon
			ABR=fils droit de ABR
		        
      Si ABR est vide
      	renvoyer Faux  
		Sinon
			renvoyer Vrai


recherche récursive :
	ABR : un arbre binaire de recherche
	v: la valeur à chercher dans l'arbre
	Renvoie Vrai si v est présente dans ABR, Faux sinon

	Si v = la racine de l'ABR
		renvoyer Vrai
	Sinon 
		Si v<la racine de ABR et fils gauche de ABR n'est pas vide
			renvoyer recherche recursive de v dans le fils gauche de ABR 	
		Sinon si v>la racine de ABR et fils gauche de ABR n'est pas vide
			renvoyer recherche recursive de v dans le fils droit de ABR
		Sinon
			renvoyer Faux

Et bien sûr, n'oubliez pas de tester vos méthodes !

SOLUTION

Applications : un peu d'économie...

Présentation du problème et des données

Nous allons utiliser les ABR pour classer des données plus concrètes : Nous allons classer les pays du monde par ordre de PIB/habitant.

Nous disposons de ces données pour 212 pays du monde (il en manque quelques uns qui ne communiquent pas ces chiffres : Corée du nord, paradis fiscaux...), dans le fichier csv pib.csv contenant, dans cet ordre :

Le nom du pays
La valeur de son PIB/habitant en US$
La valeur de son rang au niveau mondial

Le code ci-dessous permettra de récupérer les données du fichier csv et de les placer dans un tableau de tableaux :


import csv

liste_payspib = []

with open("pib.csv", 'r', encoding='utf-8') as f:
    lecteur = csv.reader(f, delimiter=',')
    for ligne in lecteur :
        liste_payspib.append(ligne)

Construire l'arbre

Vous devez maintenant construire l'arbre qui va contenir ces données.
Mais, si l'arbre ne contient que les rangs des pays, cela n'a que très peu d'intérêt... Dans cette application, les étiquettes des nœuds de l'ABR ne sont pas des entiers mais des listes du type :


['Mongolie', '4295', '129']

Comme la construction d'un ABR nécessite une relation d'ordre entre ses éléments, les comparaisons ne se feront que sur le dernier élément de ces listes.

Vous devez maintenant :

Écrire la méthode inserer_pays qui permette de construire l'ABR
Construire l'ABR correspondant
L'afficher grâce à la méthode dessinePaysdéjà présente dans la classe Arbre

Dans l'éditeur ci-dessous, le fichier pib.csv est ouvert directement à partir du site.

import csv from classe_arbre import * liste_payspib = [] with open("fichiers/pib.csv", 'r', encoding='utf-8') as f: lecteur = csv.reader(f, delimiter=',') for ligne in lecteur : liste_payspib.append(ligne) class ABR(Arbre): def inserer_pays(self, liste): pass

SOLUTION

Rechercher le 111eme pays

Maintenant que l'ABR est construit (même s'il n'est pas très lisible...), il faut être capable de rechercher un élément dans ce tableau.

Vous devez coder une méthode recherche_pays(ABR, r) décrite ci-dessous :


recherche_pays(ABR, r)
	ABR : un ABR donc les étiquettes des nœuds sont des listes du type ['Mongolie', '4295', '129']
	r: une valeur de rang à chercher
	la méthode trouve le pays de rang r et renvoie la liste le décrivant.
	S il n y a pas de pays de rang r la fonction renvoie Vide

Vous pourrez bien sur vous aider des deux méthodes codées précédemment.

def recherche_pays(ABR: ABR, r: int)->list: pass

SOLUTION

Comparaison avec une liste triée...

Nous arrivons à la fin de notre première réflexion sur les arbres, et sur les ABR. Cette structure est hiérarchique par nature, contrairement à un tableau par exemple.
Nous allons tenter de comparer un ABR et une liste triée.

Comment se nomme l'algorithme qui permet de trouver un élément dans une liste triée ?
Quelle est sa complexité dans une liste de longueur n ?
Quelle est l'ordre de grandeur de la hauteur d'un ABR contenant n données ?
Quelle est la complexité de la recherche dans un ABR contenant n données ?

SOLUTION

Si vous avez répondu correctement à ces questions, vous ne devez pas bien voir l'intérêt d'un ABR par rapport à une liste triée... Intéressons nous à l'évolution de ces structures :

Quelle est la complexité de l'ajout d'un élément dans une liste triée ?
Quelle est la complexité de l'ajout d'un élément dans un ABR ?

SOLUTION