TP : partition de l'espace

Ou voir qu'un arbre n'est pas forcément binaire !...

Introduction

Le problème de la partition de l'espace se pose en informatique dans de nombreux domaines, dès lors que l'on a une grande quantité de données à considérer dans un espace donné, comme par exemple :

la gestion des collisions dans un jeu vidéo, entre le "sprite" représentant le joueur et ceux représentant les ennemis, les obstacles du décor, etc...
la détermination des k plus proches points d'intérêt ( comme des restaurants ) parmi une multitude sur une carte
la compression d'image de grande taille
...

Nous allons prendre l'exemple de la gestion des collisions : si le nombre de sprites à l'écran est très élevé, il va être très coûteux de tester la collision avec chacun de ces sprites; il serait plus judicieux de ne tester la collision qu'avec ceux qui sont dans le voisinage le plus proche...mais alors, comment déterminer ceux-ci ?

Principe

Partition de l'espace

On utilise une structure de donnée arbre quaternaire ( = quadtree en anglais ), c'est à dire un arbre de degré 4 ( chaque nœud, sauf les feuilles, a 4 enfants ).

L'idée va être de découper récursivement l'espace en zone de plus en plus petites, et de placer les points qui sont dans ces zones comme données stockées dans le quadtree.

Considérons les 3 cartes ci-dessous :

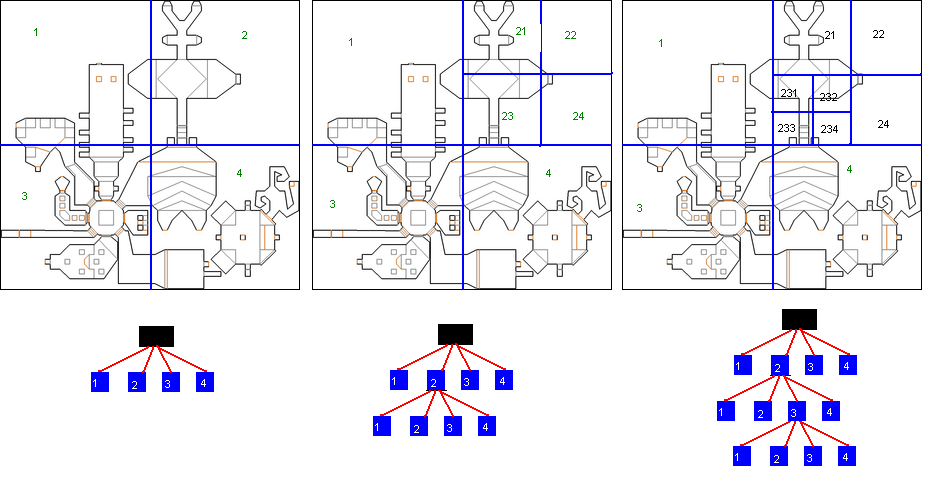
la première carte est celle de l'espace entier, que l'on découpe en 4 zones de taille identique, 4 fois plus petites ( traits bleus ); les nouvelles zones ainsi créées sont appelées 1, 2, 3 et 4.

En mémoire, la racine de l'arbre quaternaire correspondra à l'espace entier, et chacun de ses 4 enfants à une de ces 4 zones.
dans la carte du milieu, on a divisé la zone 2 en 4 zones identiques, nommées 21, 22, 23 et 24.

Ces 4 zones correspondront aux 4 enfants du nœud représentant la zone 2.
enfin, la dernière carte montre la division de la zone 23 en 4 zones identiques, correspondant aux 4 enfants du nœud de la zone 23.

Et ainsi de suite, et ce de même pour toutes les autres zones : en arrivant à la zone de plus petite division ( voir ci-dessous le cas de base de cette découpe ), on stockera alors dans une feuille de l'arbre les points qui sont dans cette zone

Dans cette structure, seules les feuilles stockent donc des données, pas les nœuds de hauteur inférieure.

Implémentation Python d'un quadtree

On choisira l'implémentation POO suivante :


class QuadTree:

    def __init__(self, x0, y0, l, h):
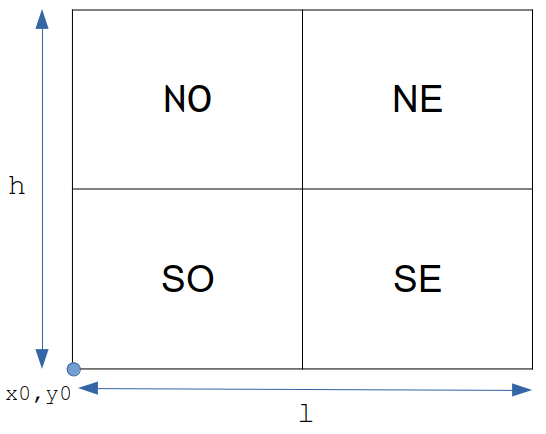
        self.x0 = x0 # coordonnées du sommet en bas à gauche de la zone correspondant à ce quadtree
        self.y0 = y0
        self.l = l # largeur de la zone
        self.h = h # hauteur de la zone
        self.NO = None # les 4 fils de ce quadtree, initialisés à None (NO = nord-ouest, NE = nord-est, etc...)
        self.NE = None
        self.SE = None
        self.SO = None
        self.points = [] # la liste des points stockés dans ce quadtree, donc appartenant à la zone correspondante

Quand on arrive sur une feuille, les quatre pointeurs vers les Quadtree fils seront None.
Comme ces pointeurs seront soit tous nuls, soit tous non nuls, pour vérifier qu'un nœud est une feuille, il suffira donc de regarder le premier fils, et voir s'il est None ou pas.

D'après le principe énoncé ci-dessus, L'attribut self.points sera donc vide, sauf pour les feuilles.

Algorithme de découpage

Comment découper un Quadtree ? Jusqu'où continuer à découper ?

L'idée est de définir une constante MAX_POINTS, qui sera le nombre maximal de points qu'on veut stocker dans une zone "élémentaire" ( = celle de plus petite taille ).
Par exemple, on voudra stocker au maximum 10 points, parce que l'on va chercher à tester les collisions sur les 10 voisins les plus proches.

Cependant, la répartition des points étant aléatoire, on n'aura pas forcément MAX_POINTS points dans chaque feuille, c'est un maximum ...

on créé un quadtree, dans la racine duquel on insère tous les points de l'espace.
la méthode d'insertion va alors insérer récursivement tous ces points dans le quadtree :
- si la liste de ces points a moins de MAX_POINTS éléments, alors on est arrivé à une feuille : on stocke l'ensemble des points dans la feuille.
- sinon :
  - on répartit les points dans 4 listes, correspondant aux zones des 4 fils; pour cela, on utilisera une méthode is_in qui permettra de déterminer si un point donné se trouve dans telle ou telle zone.
  - une fois la répartition faite, on divise alors le quadtree en créant les 4 quadtree fils.
  - et on insère récursivement la liste respective des points dans chacun de ces quadtree.

Bien entendu, la construction d'un quadtree peut prendre du temps; mais, pour la carte des objets fixes dans un jeu vidéo, la construction peut se faire une fois pour toutes au chargement de la carte, voire même le quadtree peut être stocké avec la carte directement.

Utilisation du quadtree pour la recherche des plus proches voisins

Une fois le quadtree créé, il est évident de l'utiliser pour déterminer les MAX_POINTS plus proches voisins : il faut "descendre" récursivement dans l'arbre, jusqu'à atteindre la feuille correspondant à la zone dans laquelle se trouve le point; à ce moment, on renvoie simplement la liste des points stockés dans le quadtree correspondant.

cas de base : on est arrivé à une feuille, on renvoie la liste des points stockés dans cette feuille
cas général :
- si le point se trouve dans la zone correspondant au fils SO, alors on recherche récursivement dans le fils SO
- sinon si le point se trouve dans la zone correspondant au fils SE, alors on recherche récursivement dans le fils SE
- etc...

Application

Téléchargez et enregistrez le fichier quadtree_eleve.py qui vous servira de base de départ.

Dans ce fichier on trouve :

une classe Point modélisant un point de l'espace
une classe QuadTree dont les méthodes seront à compléter; cette classe contient le constructeur et la méthode is_in citée ci_dessus : pour son utilisation, étudier la docstring de cette méthode.
une méthode afficher qui permettra d'afficher le découpage de l'espace et les points dans chaque zone à l'aide d'un graphique Matplotlib
une fonction afficher_voisins qui permettra d'afficher les résultats de la recherche de voisins d'un point donné, à l'aide d'un graphique Matplotlib : les points à tester apparaissent en bleu, le point "témoin" en vert, et les points les plus proches en rouge.

Construction du quadtree

On considérera un espace plan de taille 256 x 256; la coordonnée (0, 0) se trouve en bas à gauche de cet espace.

Compléter la méthode inserer de la classe Quadtree, qui implémente l'algorithme de découpage présenté ci-dessus.
créer une liste de 50 objets Point dont les coordonnées seront déterminées aléatoirement dans les limites de la taille de l'espace.
instancier le quadtree, et y insérer la liste des points.
afficher le quadtree

Détermination des plus proches voisins

compléter la méthode trouver_voisins de la classe QuadTree qui implémente l'algorithme de recherche ci-dessus
instancier un objet Point qui sera le "témoin" autour duquel on cherchera les plus proches voisins.
afficher le résultat renvoyé par cette méthode !.
modifier le nombre de points maximal par feuille, le nombre de points, la taille de l'espace, etc...

Prolongement

Vous pouvez prolonger ce travail en écrivant une fonction qui implémente une recherche "naïve" de n plus proches voisins dans une liste de points, et comparer à l'aide du module timeit le temps d’exécution de chacune des deux approches vues dans ce TP.

Quelle est la complexité de chacun des algorithmes de recherche utilisé ?

Correction

Une correction possible pour ce TP.