Arbres binaires

Introduction

Nous avons vu de façon générale, les arbres dans la partie précédente. Nous allons restreindre un peu notre champ d'action en nous consacrant maintenant uniquement aux arbres binaires.

Les arbres binaires sont des arbres de degré 2, donc :

Les nœuds d'un arbre binaire ont au plus deux fils.
On distinguera le fils gauche et le fils droit.

Comme on peut le remarquer dans la définition ci-dessus, la structure des arbres ( et en particulier des arbres binaires ) est récursive !

Et oui un arbre binaire, c'est :

un nœud racine
un arbre binaire que l'on devrait appeler "sous-arbre gauche", mais que l'on qualifiera simplement de "fils gauche".
un arbre binaire que l'on appellera "fils droit"

Propriétés

Avant de continuer notre réflexion sur les arbres binaires, nous allons tenter de comprendre pourquoi cette structure hiérarchique est intéressante.

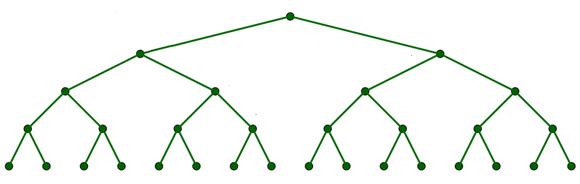
L'arbre ci-dessous est un arbre binaire un peu particulier car il est complet, c'est à dire que les nœuds de cet arbre ont tous exactement un fils gauche et un fils droit, sauf les feuilles bien entendu...

arbre binaire complet

Quelle est la hauteur de cet arbre ?
Quelle est la taille de cet arbre ?
Combien de données peuvent être stockées dans cet arbre ?
Combien de branches doit-on parcourir au maximum pour atteindre n'importe quelle donnée de cet arbre ?
Quelle est la hauteur d'un tel arbre de taille 63, 127, 255 ?
De façon générale quelle est la hauteur d'un arbre binaire complet contenant n nœuds ?

SOLUTION

Implémentation

Vous avez déjà implémenté ou mis en œuvre de nombreux types abstraits de données linéaires : piles, files, listes...
L'arbre binaire n'est pas un type linéaire, mais il est tout à fait possible de l'implémenter en python.
Dans certains cas il est intéressant d'implémenter un arbre dans une liste Python. Cependant dans cette situation, il n'est pas forcément facile de trouver les fils d'un nœud, et on perd l'intérêt de la structure récursive.

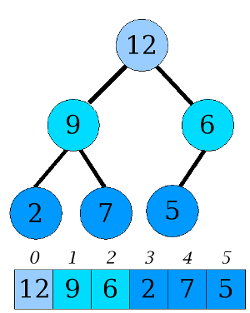
Nous choisirons une implémentation en POO qui ressemble à celle utilisée pour implémenter les listes chaînées :


class Arbre:
    def __init__(self, valeur = None, filsgauche = None, filsdroit = None):
        self.valeur = valeur
        self.filsgauche = filsgauche
        self.filsdroit = filsdroit

On notera bien que, dans cette classe :

self peut représenter aussi bien l'arbre complet qu'un sous-arbre quelconque
self.valeur est l'étiquette de la racine de l'arbre ou du nœud-racine du sous-arbre
self.filsgauche et self.filsdroit sont des objets de type Arbre, enfants de la racine ou du nœud-racine du sous-arbre
si la racine ou le nœud-racine du sous-arbre n'a pas d'étiquette, alors self.valeur = None
si la racine ou le nœud-racine du sous-arbre n'a, par exemple, pas de fils droit alors self.filsdroit = None

Afin de faciliter votre travail, une méthode d'affichage des arbres binaires a déjà été implémentée. Vous n'aurez donc, pour utiliser cette nouvelle classe, qu'a télécharger le fichier classe_arbre.py à l'enregistrer et à l'importer en début de script.

Vous pouvez utiliser ce module aussi bien avec Pyzo qu'en ligne dans les éditeurs.

dans le premier cas, rappelez-vous que ce fichier et votre script doivent être dans le même répertoire.
Dans le deuxième cas, pensez au préalable à l'enregistrer dans le système de fichiers virtuel ( bouton Charger un fichier ) pour qu'il soit ensuite disponible pour les scripts. Importer également le module de dessin Matplotlib ( bouton Importer un module )

Pour comprendre le fonctionnement de la classe Arbre, construisez et affichez l'arbre hetre ci-contre.

L'affichage se fait grâce à la méthode dessine() de la classe.

from classe_arbre import * hetre = ... hetre.dessine()

SOLUTION

Une application : les arbres arithmétiques

Nous avons vu dans la première partie qu'il était possible de coder une expression arithmétique dans un arbre binaire. En effet l'arithmétique correspond à la combinaison d'un opérateur (+, -, x, /) et de deux opérandes (entiers, réels...).

Par exemple l'arbre arithmétique ci-contre représente l'expression (x+1)(3y+2).

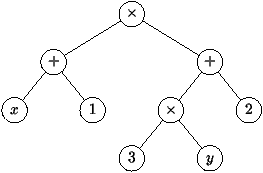
Construisez cet arbre grâce à la classe Arbre.

from classe_arbre import * arit = ... arit.dessine()

SOLUTION

L'intérêt de construire un tel arbre à partir d'une expression arithmétique est multiple :

C'est utile pour calculer cette expression (il faut bien comprendre qu'ici "(x+1)(3y+2)" est de type str et que si l'on connaît les valeur de x et de y il n'est pas simple de calculer sa valeur).
Cela peut être utile pour résoudre de manière formelle une équation
Cela peut être utile également pour calculer de manière formelle la dérivée d'une expression.

Vous trouverez ci-dessous l'algorithme (récursif) qui permet de calculer la valeur d'une expression arithmétique contenue dans un arbre binaire :


méthode calcule(arbre arithmétique)

	entrée : arbre binaire arithmétique
	sortie : valeur de l'expression arithmétique
	
	Si l'arbre est une feuille alors :
		renvoyer valeur de la feuille
	Sinon si l'étiquette du nœud est '+' alors:
		renvoyer calcule(filsgauche) + calcule(filsdroit)
	Sinon si l'étiquette du nœud est '-' alors:
		renvoyer calcule(filsgauche) - calcule(filsdroit)
	Sinon si l'étiquette du nœud est '*' alors:
		renvoyer calcule(filsgauche) * calcule(filsdroit)
	Sinon si l'étiquette du nœud est '/' alors:
		renvoyer calcule(filsgauche) / calcule(filsdroit)

Vous devez coder une méthode calcule(self) qui permet d'évaluer la valeur d'une expression arithmétique présentée sous forme d'arbre binaire arithmétique.
Vous testerez cette méthode sur l'arbre codé précédemment, en donnant au préalable des valeurs aux variables x et y ( attention alors lors de la construction de l'arbre ! ).

Mais vous ne pouvez pas "compléter" la classe Arbre présente dans le fichier classe_arbre.py que vous avez importé...
Vous allez en fait créer une sous classe Arbrearith qui héritera de toutes les propriétés de la classe Arbre.
Concrètement (l'héritage n'est pas au programme de la TNSI, mais ce n'est pas compliqué...), vous allez créer une nouvelle classe à partir de la classe Arbre, qui disposera de ses méthodes mais qui leur rajoutera ses propres fonctionnalités :

	
class Arbrearith(Arbre):
	''' La classe Arbrearith hérite des méthodes de Arbre '''
	
	def calcule(self): # mais elle implémente aussi ses propres fonctionnalités
		...

Le constructeur d'Arebrearith est celui de la classe Arbre, et la méthode dessine peut également être utilisée.

from classe_arbre import * class Arbrearith(Arbre): def calcule(self): pass x = 2 y = 3 # par exemple... arit = Arbrearith( ... ) # utiliser les variables x et y pour construire l'arbre arit.dessine() print(arit.calcule())

SOLUTION

Un problème binaire : le morse

Même si le morse est un langage binaire un peu démodé, il peut être intéressant de se pencher sur la possibilité d'un décodage rapide de tel message pour voir l’intérêt des arbres binaires.

Nous baserons notre travail sur le dictionnaire de morse ci-dessous :


dicomorse = { 'A':'.-', 'B':'-...','C':'-.-.', 'D':'-..', 'E':'.','F':'..-.', 'G':'--.', 'H':'....','I':'..','J':'.---','K':'-.-','L':'.-..', 'M':'--', 'N':'-.','O':'---', 'P':'.--.', 'Q':'--.-','R':'.-.', 'S':'...','T':'-','U':'..-', 'V':'...-', 'W':'.--','X':'-..-', 'Y':'-.--', 'Z':'--..','1':'.----', '2':'..---', '3':'...--','4':'....-', '5':'.....', '6':'-....','7':'--...', '8':'---..', '9':'----.','0':'-----', ', ':'--..--', '.':'.-.-.-','?':'..--..', '/':'-..-.', '-':'-....-','(':'-.--.', ')':'-.--.-',' ':'.......'}

Construire l'arbre binaire

La première chose à faire est de transformer ce dictionnaire en arbre binaire.
La règle de construction pour une lettre sera la suivante :

On part de la racine de l'arbre
Si le premier caractère est un trait on suit la branche de droite
Si le premier caractère est un point on suit la branche de gauche
On traite ainsi tous les traits et les points du caractère
l'étiquette du nœud final sera la lettre codée

On doit ainsi obtenir l'arbre suivant :

arbre morse

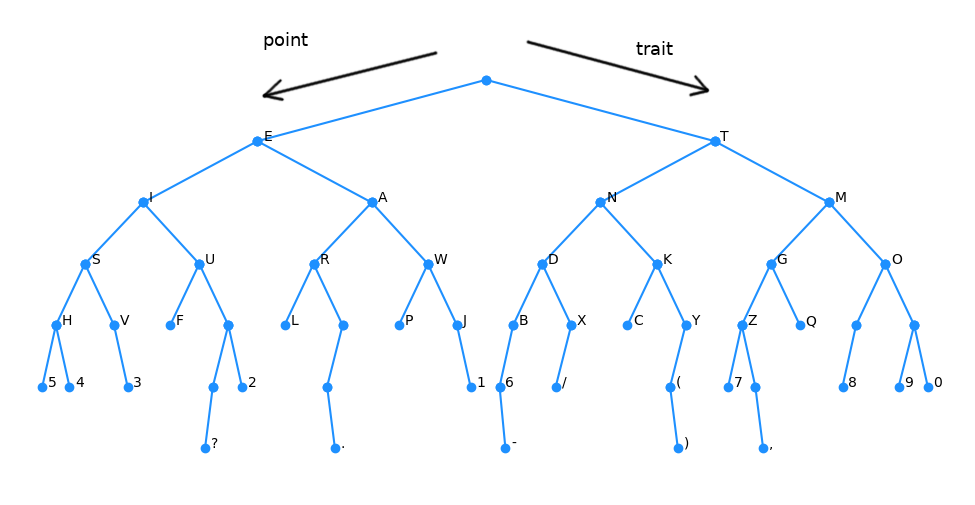
Il va donc falloir "descendre dans l'abre" pour parcourir ses différentes branches...

Voyez alors l'analogie qu'il y a avec la manière que vous avez utilisé pour vous déplacer dans une liste chaînée :


maillon = tete                    # référence vers la tête de la liste
tant que maillon n'est pas None:  # tant qu'on n'est pas arrivé au dernier maillon,
	maillon = le maillon suivant   # on passe au maillon suivant.

Le même principe peut alors être utilisé ici, à la différence près qu'il y a un choix à faire dans la branche où l'on souhaite descendre :


noeud = racine                        # référence vers la racine de l'arbre
tant que noeud n'est pas None:        # tant qu'on n'est pas arrivé à une feuille,
	si on veut aller à gauche:
		noeud = le fils gauche du noeud
	sinon:
		noeud = le fils droit du noeud

Vous allez maintenant devoir compléter la fonction creer_arbre_morse ci-dessous, qui permet de créer cet arbre binaire.
Pour vous faciliter cette tache de création, vous pourrez utiliser les deux méthodes de la classe Arbre :


insertion_gauche(valeur): # permet d'insérer un nœud-fils à gauche du nœud courant, en précisant son étiquette
			
insertion_droite(valeur):  # idem à droite

from classe_arbre import * def creer_arbre_morse(): dicomorse = { 'A':'.-', 'B':'-...','C':'-.-.', 'D':'-..', 'E':'.','F':'..-.', 'G':'--.', 'H':'....','I':'..','J':'.---','K':'-.-','L':'.-..', 'M':'--', 'N':'-.','O':'---', 'P':'.--.', 'Q':'--.-','R':'.-.', 'S':'...','T':'-','U':'..-', 'V':'...-', 'W':'.--','X':'-..-', 'Y':'-.--', 'Z':'--..','1':'.----', '2':'..---', '3':'...--','4':'....-', '5':'.....', '6':'-....','7':'--...', '8':'---..', '9':'----.','0':'-----', ', ':'--..--', '.':'.-.-.-','?':'..--..', '/':'-..-.', '-':'-....-','(':'-.--.', ')':'-.--.-', ' ':'.......'} racine = Arbre(' ') noeud_courant=racine for clef in dicomorse: for car in dicomorse[clef]: if car=='.': ....# insérer un fils ....# descendre dans l'arbre if car=='-': ....# insérer un fils ....# descendre dans l'arbre .... # etiqueter le noeud noeud_courant=racine return racine

Vous vérifierez que votre fonction est valide en affichant l'arbre ainsi construit.

SOLUTION

Décoder un message

Une fois cet arbre construit, nous allons l'utiliser pour décoder un message en morse.

Parlons un peu de complexité

Pour décoder un message en morse, il est normalement nécessaire de parcourir tout le dictionnaire de morse pour trouver le caractère qui correspond au code reçu.
Il est donc nécessaire, au pire, de faire 43 comparaisons ( = le nombre de caractères présents dans notre dictionnaire de morse ).

Pour trouver un caractère dans l'arbre que vous venez de construire, il suffit au contraire de suivre le "bon" chemin. Dans le pire des cas on doit faire 6 comparaison !
On voit ainsi le gain qu'il y a si on cherche ensuite "souvent" à décoder un code morse.
Mais bien sur ici le morse est une excuse pour voir plus loin 😏...

Imaginons une structure de données basée sur le même principe que l'arbre morse.

Si l'on fait une recherche sans l'arbre dans n caractères, la complexité sera en O(n).

Quelle sera la complexité de la recherche dans l'arbre en fonction de n ?

SOLUTION

Décodons !

Maintenant que vous maîtrisez le concept, il ne vous reste plus qu'à l'utiliser pour décoder un message en morse.

La docstring de la fonction à compléter est présentée ci-dessous, avec les annotations de type.
A vous de la coder complètement.

from classe_arbre import * def creer_arbre_morse(): # code précédent pass def decode_morse(code: str, arbrebin: Arbre)->str: """ Fonction pour décoder un caractère codé en morse Entrées : code : un code composé de '-' et de '.' codant un caractère selon l'alphabet morse arbrebin : l'arbre binaire ('.' à gauche, '-' à droite) correspondant au dictionnaire de morse Sortie : le caractère décodé """ pass

Utiliser ensuite votre fonction :

pour décoder le message : "... --- ... " qui doit donner 'SOS'

pour décoder le message :

	
".--. .- ... ... .. --- -. -. .- -. - ....... .-.. .- ....... -. ... .. "

Vous pourrez utiliser la méthode de chaîne str.split(' '), qui renvoie la liste Python des "mots" d'une chaîne en la découpant selon le caractère ' ' ( espace ).

SOLUTION