contrairement à ce que le nom suggère, la complexité n’est pas une mesure de si un algorithme est « simple » ou « complexe » d’un point de vue humain, mais une mesure de sa durée d’exécution ( son "coût" ).
Le temps d’exécution d’un programme dépend :
... et aussi de la qualité de la programmation !
Beaucoup de paramètres, dont certains ne sont pas faciles à évaluer...Donc :
Et on parle toujours de la complexité d’un ALGORITHME, pas d’un programme réel.
n est une évaluation de la TAILLE DES DONNÉES, c’est-à-dire le nombre de données que devra manipuler l’algorithme.
On doit essayer de choisir comme taille ( la ou ) les dimensions les plus significatives.
Par exemple, selon que le problème est modélisé par :
Le choix d’une structure de données à une grande influence sur l’efficacité d’un algorithme ! !
Dans l’idéal, il faut compter toutes les “opérations” élémentaires impliquées dans l’algorithme.
Cependant, toutes les instructions n’ont pas le même coût en temps !
Il faut donc choisir quelles opérations compter : des opérations simples et indépendantes de l’implantation
de l’algorithme : affectations, comparaisons, ....
Il n’est pas toujours évident de compter exactement le nombre d’opérations impliquées dans les algorithmes. On se contente de trouver des approximations.
Et pour simplifier, on fait l’hypothèse que toutes ces opérations élémentaires ont le même coût en temps.
Un même algorithme sert en général à résoudre divers problèmes qui ne présentent pas le même coût en temps :
Par exemple, dans le cas d'un algorithme qui insère une valeur dans un tableau :
On préfère généralement majorer la complexité d'un algorithme, c’est-à-dire que l’on cherche une borne supérieure que l’on est sûr de ne jamais dépasser : c'est la complexité d’un algorithme dans le PIRE cas.
Ce n’est pas très intéressant d’étudier la complexité si la taille du problème est petite : l’efficacité d’un algorithme n’est un enjeu important que sur les gros problèmes.
Mais on ne sait pas où est la limite entre "petits" et "gros" problèmes !!
Conséquence : on ne s’intéresse qu'à la complexité asymptotique des algorithmes, c'est à dire quand la taille n du problème tend vers les très grandes valeurs ( voire vers ∞ ).
La complexité est exprimée sous la forme O(f(n)) ( "grand O de f de n" ), où f(n) est une fonction de n qui majore le nombre d'opérations élémentaires de l'algorithme, c'est à dire que le nombre d'opérations sera, pour de très grandes valeurs de n, toujours inférieur ou égal à la valeur de f(n) multipliée par une constante :
nombre d'opérations ≤ k . f(n)
Exemples :
| Nombre d'opérations | Complexité |
|---|---|
| 1 000 000 | O(1) |
| n | O(n) |
| 10.n | O(n) |
| 5.n3 + 12.n2 + 8 | O(n3) |
| n10 | O(2n) |
La connaissance de la complexité d'un algorithme unique n'a pas beaucoup d'intérêt tant qu'on ne la compare pas à celle d'un autre algorithmie faisant le même travail; le classement des complexités en classes de complexité permet de faire cette comparaison et de déterminer quel est l'algorithme le plus efficace.
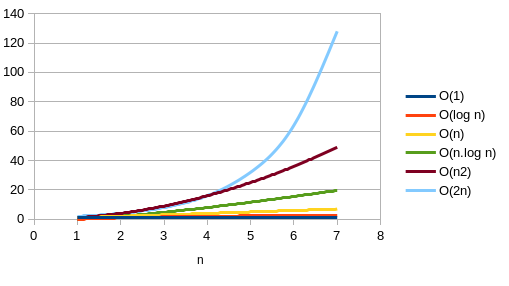
De la meilleure à la pire :
| Nom | Notation | Durée quand on double la taille des données à traiter | Exemple(s) |
|---|---|---|---|
| constant | O(1) | durée inchangée ! | opérations élémentaires : affectation, comparaison,... |
| logarithmique | O(log n) | prend seulement une étape de plus | recherche dichotomique |
| linéaire | O(n) | prend 2 fois plus de temps | recherche séquentielle, calcul de la longueur d'une liste,... |
| quasi-linéaire | O(n.log n) | prend 2 fois de temps + n étapes supplémentaires | tri fusion |
| quadratique | O(n2) | prend 4 fois plus de temps | tri à bulles, tri par insertion,... |
| polynomial | O(nk) | prend 2k fois plus de temps | avec k fixé ( k > 3 ) |
| exponentiel | O(kn) | prend tellement de temps que c'en est inconcevable... à fuir ! | Fibonacci récursif. |
| factorielle | O(n!) | prend tellement de temps que c'en est inconcevable... à fuir ! | Calcul de la factorielle d'un entier |