def chaine_multiple(motif, n):
if n == 1:
return motif
else:
if n%2 == 0:
return chaine_multiple(motif, n//2) + chaine_multiple(motif, n//2)
else:
return motif + chaine_multiple(motif, n//2) + chaine_multiple(motif, n//2)
Si on raisonne sur un exemple :
Donc :
def puissance(x, n):
if n == 1:
return x
else:
return x*puissance(x, n-1)
def puissance(x, n):
if n == 1:
return x
else:
if n%2 == 0:
return puissance(x**2, n//2)
else:
return x*puissance(x**2, n//2)
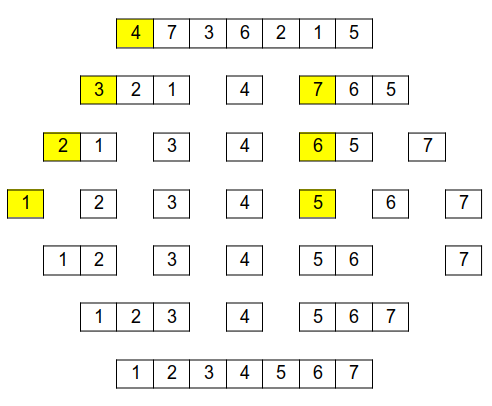
def tri_rapide(L):
if len(L) == 0:
return []
pivot = L.pop(0) # on retire le pivot du tableau, pour ne pas le traiter deux fois.
gauche = [elt for elt in L if elt <= pivot]
droite = [elt for elt in L if elt > pivot]
gauche = tri_rapide(gauche)
droite = tri_rapide(droite)
return gauche + [pivot] + droite
def rech_max(L, g, d):
if g == d:
return L[g]
else:
m = (g + d)//2
max_g = rech_max(L,g, m)
max_d = rech_max(L, m+1, d)
if max_g > max_d:
return max_g
else:
return max_d
def rech_min(L, g, d):
if g == d:
return L[g]
else:
m = (g + d)//2
min_g = rech_min(L,g, m)
min_d = rech_min(L, m+1, d)
if min_g < min_d:
return min_g
else:
return min_d
L'algorithme revient en fait à découper la liste en n éléments que l'on compare chacun à un maximum ( ou un minimum ), l’algorithme est donc en O(n) ( ce qui est exactement la même complexité que la recherche séquentielle...)
Si on recherche le maximum OU le minimum, on réalise donc à chaque fois n comparaisons, ce qui revient au total à 2n comparaisons pour la recherche successive de l'un, puis de l'autre.
L'idée : au lieu de ne renvoyer que le maximum OU le minimum, on renvoie les deux en même temps ( sous forme d'un tuple de deux éléments ).
De même, la recherche de ces deux valeurs se fera en même temps lors des appels récursifs de la fonction sur chaque moitié de tableaux.
Par contre, il faut prévoir un cas de base qui n'existait pas précédemment : comme le maximum et le minimum d'un tableau sont a priori deux éléments différents, il faut donc gérer la situation où, lorsque l'on a "réduit" le tableau a deux éléments, lequel de ces deux correspond au minimum, et lequel au maximum :
def minmax(L, g, d):
if g == d:
return L[g], L[g]
elif d == g + 1:
if L[g] > L[d]:
return L[g], L[d]
else:
return L[d], L[g]
else:
m = (g + d)//2
max_g, min_g = minmax(L, g, m)
max_d, min_d = minmax(L, m + 1, d)
if max_g > max_d:
maxi = max_g
else:
maxi = max_d
if min_g < min_d:
mini = min_g
else:
mini = min_d
return maxi, mini
Ce deuxième cas de base correspond ici aux lignes 5 à 9.
Moins évidente à établir de manière générale, travaillons plutôt sur un exemple :
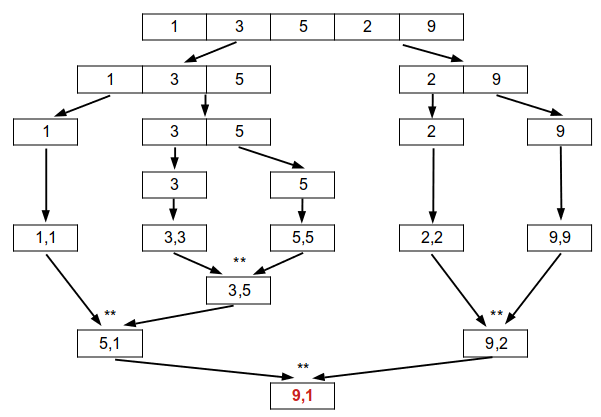
Pour rechercher simultanément le maximum et le minimum, on fait à chaque appel récursif 2 comparaisons ( ** sur l'image ci-dessus ); en totalité, on constate que l'on aura donc fait 8 comparaisons, à comparer aux 10 que l'on aurait fait ( 2n ) avec la recherche successive des deux valeurs.
Cela ne paraît pas beaucoup, mais on montre qu'en général, on fait dans ce cas 3/2n comparaisons, ce qui est donc intéressant pour de grandes valeurs de n ( comme toujours ) ...mais à condition que l'on recherche effectivement le maximum ET le minimum, sinon la recherche séquentielle reste bien entendu plus efficace !
def rech_recurs(n, L):
if len(L) == 1 :
if L[0] == n:
return True
else:
return False
mid = len(L)//2
gauche = [L[i] for i in range(0,mid)]
droite = [L[i] for i in range(mid, len(L))]
return rech_recurs(n, gauche) or rech_recurs(n, droite)
La complexité est la même que la recherche séquentielle ( O(n) ), puisque là aussi, on découpe la liste en n éléments que l'on compare à la valeur recherchée...
Ces deux exemples reviennent en réalité à parcourir l'intégralité de la liste : on remplace donc la recherche séquentielle en O(n)...par un algorithme lui aussi en O(n) 😧 !!
L'approche "diviser pour régner" n'apporte donc rien à ces problèmes; pour qu'elle soit intéressante, il faut donc que cette approche diminue fortement le nombre d'opération à effectuer...