fonction recherche_sequentielle(L: tableau, n:valeur):
tant que l'on n'a pas trouvé la valeur ET que l'on n'est pas arrivé à la fin du tableau:
si élément courant == n :
alors on a trouvé la valeur
sinon:
on passe à l'élément suivant
renvoyer Vrai ou Faux selon que l'on a trouvé ou pas la valeur
return multiples"On utilise dans ce cas une boucle for (= boucle bornée), dont on sortira prématurément dans le cas où l'on trouve la valeur dans le tableau :
def recherche_seq(L, n):
for i in range(len(L)) : # parcours de la liste par indice, ce qui permettra de renvoyer l'index de la valeur dans la liste dans le cas où on la trouve
if L[i] == n:
return i
return -1 # pour le cas où la valeur n'a pas été trouvée
return"Dans un tel algorithme, on ne sait pas à l'avance combien d'élément(s) du tableau on va devoir parcourir :
Dans une telle situation, c'est logiquement plutôt une boucle while (= boucle non bornée) qu'il faut utiliser.
Dans cette boucle, il y aura deux conditions à tester :
def recherche_seq(L, n):
i = 0 # indice de l'élément courant
flag = False # variable "drapeau", initialisée à 'False', et qui "basculera" à 'True' si on trouve la valeur à l'indice i
while i != len(L) and not flag: # 'not flag' est égal à 'True' si flag = False, c'est à dire que la valeur n'a pas été trouvée.
if L[i] == n: # Si on trouve la valeur à l'indice i,
flag = True # alors on bascule le drapeau, ce qui arrêtera la boucle.
else:
i += 1 # sinon on passe à l'élément suivant.
if flag: # si 'flag' est égal à True, on a trouvé la valeur,
return i # on renvoie l'indice où elle se trouve;
else:
return -1 # sinon, la valeur n'a pas été trouvée.
On peut remarquer que l'on n'a même pas forcément besoin de la variable drapeau :
def rech_seq(L, n):
i = 0
while i != len(L) and L[i] != n: # on teste TOUT en même temps !!!
i += 1
if i != len(L): # on peut écrire simplement : 'return i if i != len(L) else -1'
return i
else:
return -1
Dans le pire des cas, la valeur recherchée se trouve à la toute fin de la liste ( ou alors pas du tout ! ) : on est donc obligé de parcourir intégralement cette dernière, soit ses n éléments : la complexité est donc en O(n).
fonction rech_dichoI(L : tableau trié, n : valeur à chercher ):
g ← indice du premier élément du tableau
d ← indice du dernier élément du tableau
tant que g <= d:
m ← (g+d)//2
si L[m] = n :
renvoyer m
sinon :
si n < L[m]:
d ← m-1
sinon ( donc si valeur > L[m] ):
g ← m+1
renvoyer -1
Si on ne trouve pas la valeur à l'indice m ( ligne 9 ), il faut donc exclure l'élément d'indice m de la recherche à l'étape suivante :

def rech_dichoI(L, n):
g = 0
d = len(L) - 1
while g <= d:
m = (g+d)//2
if L[m] == n :
return m
elif n < L[m]:
d = m-1
else:
g = m+1
return -1
La recherche dichotomique s'exprime bien plus simplement récursivement :
def rech_dichoR(L: list, n: int, g: int, d: int):
if g > d: # cas de base
return -1
m = (g+d)//2 # cas général
if L[m] == n:
return m
elif n > L[m]:
return rech_dicho_rec(L, n, m+1, d)
else:
return rech_dicho_rec(L, n, g, d-1)
print(rech_dichoR(L, 99, 0, len(L)-1)) # appel de la fonction
Il est intéressant de remarquer que la condition évaluée dans le cas de base est la négation logique de celle évaluée dans la boucle while
de l'algorithme itératif.
En effet :
while, c'est une condition pour CONTINUER la boucle.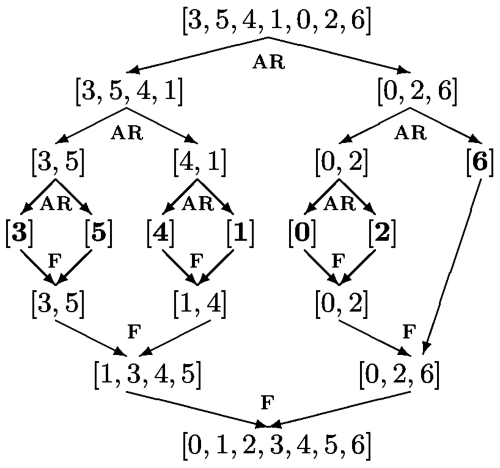
On constate donc que les appels récursifs à tri_fusion ne servent "qu'à" découper la liste jusqu'à n'arriver qu'à des listes à un seul élément.
Le renvoi de ces appels récursifs correspondent à l'appel de la fonction de fusion, qui est l'opération de tri proprement dite de deux listes, elles-mêmes triées :
fonction fusionI(L1, L2:listes triées):
L3 ← liste vide
tant qu'on n'est pas arrivé à la fin d'une des listes :
si l'élément courant de L1 est plus petit que ( ou égal à ) l'élément courant de L2:
L3 ← L3 + élément courant de L1
on passe à l'élément suivant de L1
sinon:
L3 ← L3 + élément courant de L2
on passe à l'élément suivant de L2
L3 ← L3 + liste restante non-vide
renvoyer L3
Encore plus simple à concevoir :
fonction fusionR(L1, L2:listes triées):
si on est arrivé à la fin de L1:
renvoyer L2
sinon si on est arrivé à la fin de L2:
renvoyer L1
sinon:
si l'élément courant de L1 est plus petit que ( ou égal à ) l'élément courant de L2:
renvoyer élément courant de L1 + fusionR(reste de L1, L2)
sinon:
renvoyer élément courant de L2 + fusionR(L1, reste de L2)
Voila une situation où la récursivité, bien que ne changeant rien à la complexité par rapport à l'algorithme itératif, apporte beaucoup plus de clarté et "d'élégance"à cet algorithme...
L'implémentation va dépendre du fait que les données sont structurées en "vraies" listes ou alors si il s'agit seulement de tableaux...
On peut partir du principe que, comme on manipule des listes, on dispose des primitives pop(0) et append() qui permettent respectivement de supprimer le premier élément et d'ajouter un élément
à la fin d'une liste. Si les listes sont implémentées sous forme de liste chaînée, la suppression de leur premier élément est de plus très efficace en temps ( voir le chapitre correspondant ) !
Dans la fonction de fusion, "l'élément courant" sera alors le premier élément de chaque liste, que l'on supprimera de la "bonne" liste selon le résultat de la comparaison; une des listes diminue donc d'un élément à chaque itération : l'algorithme s'arrête quand une des listes est vide, on insère alors les éléments restants de l'autre à la fin de la nouvelle liste :
def fusionI(L1, L2):
L3 = []
while len(L1) != 0 and len(L2) != 0:
if L1[0] <= L2[0]:
L3.append(L1.pop(0))
else:
L3.append(L2.pop(0))
L3 = L3 + L1 + L2 # on ajoute à la fin le "reliquat" de liste non-vide ( que ce soit L1 ou L2 )
return L3
Et pour la version récursive :
def fusionR(L1, L2):
if len(L1) == 0 :
return L2
if len(L2) == 0 :
return L1
else:
if L1[0] > L2[0]:
return [L2.pop(0)] + fusion(L1, L2)
else:
return [L1.pop(0)] + fusion(L1, L2)
On rappelle que la méthode pop() retire un élément d'une liste et renvoie cet élément : LX.pop(0) modifie donc la liste, que l'on peut ensuite passer en argument lors de l'appel récursif suivant.
Attention à la syntaxe de la concaténation d'un élément à une liste ( lignes 10 et 12 ) : on ne peut pas "ajouter" une valeur à une liste ( types incompatibles ), c'est pourquoi on concatène en réalité une liste à un
seul élément ( [LX.pop(0)] ) au reste de la liste construite par la fonction fusion().
Autre possibilité :
def fusionR(L1, L2, L3):
if len(L1) == 0 :
for elt in L2:
L3.append(elt)
return L3
if len(L2) == 0 :
for elt in L1:
L3.append(elt)
return L3
else:
if L1[0] > L2[0]:
L3.append(L2.pop(0))
return fusion(L1, L2, L3)
else:
L3.append(L1.pop(0))
return fusion(L1, L2, L3)
L'intérêt ici est d'utiliser la méthode de liste append, plus efficace que la concaténation de listes; la version récursive nécessite cependant de passer un troisième paramètre à la fonction,
la liste fusionnée, initialement vide.
Or, on ne peut pas donner à un paramètre mutable une valeur par défaut : c'est donc dans l'appel de la fonction fusionR qu'il faut directement passer un argument "liste vide" [].
listes_fusionnees = fusionR(L1, L2, [])
Le problème de l'approche précédente est que l'on modifie les listes passées en argument.
Si on ne dispose pas d'une structure de listes mais de tableaux, il faut revenir à une méthode manipulant des indices pour désigner "l'élément courant" de chaque liste :
def fusionI(L1, L2):
L3 = [] # tableau vide qui contiendra la liste fusionnée
i = 0 # indice indiquant l'élément courant dans L1
j = 0 # idem pour L2
while i != len(L1) and j != len(L2) :
if L1[i] <= L2[j]:
L3 = L3 + [L1[i]]
i = i + 1 # avance d'un élément dans L1
else:
L3 = L3 + [L2[j]]
j = j + 1 # avance d'un élément dans L2
if i == len(L1): # si on est arrivé à la fin de L1
while j != len(L2):
L3 = L3 + [L2[j]] # ajout des éléments restants de L2
j = j + 1
else:
while i != len(L1): # sinon, ajout des éléments restants de L1
L3 = L3 + [L2[j]]
i = i + 1
return L3
Oui, plus délicat à coder...et encore, on ne respecte pas complètement le type tableau de taille fixe, puisque L3 est en réalité un tableau initialement vide, auquel on ajoute à la fin
les éléments un par un ( ce qui crée en fait un nouveau tableau à chaque ajout ).
L'approche la plus efficace aurait été de créer initialement un tableau L3 de taille définie, égale à la taille cumulée de L1 et L2, et à ensuite affecter
à chaque élément de ce tableau une valeur.
Mais cela oblige à rajouter un index supplémentaire pour parcourir le tableau L3, et le code devient franchement compliqué ( vous pouvez le consulter ici ); on se contentera donc de la présente version qui est un "compromis" entre respect des types et clarté du code !
Et la version récursive ( plus simple aussi ! ) :
def fusionR(L1, L2, i = 0, j = 0):
if i == len(L1):
return [L2[k] for k in range(j, len(L2))]
elif j == len(L2):
return [L1[k] for k in range(i, len(L1))]
else:
if L1[i] <= L2[j]:
return [L1[i]] + fusionR(L1, L2, i+1, j)
else:
return [L2[j]] + fusionR(L1, L2, i, j+1)
Le plus dur est fait ! Il est alors très facile de coder l'algorithme de tri-fusion proprement dit :
def tri_fusion(L):
if len(L) == 1 :
return L
mid = len(L)//2
gauche = [L[i] for i in range(0, mid)]
droite = [L[i] for i in range(mid, len(L))]
gauche = tri_fusion(gauche)
droite = tri_fusion(droite)
return fusion(gauche, droite) # version itérative ou récursive, peu importe !