Correction : programmation dynamique

Principes

La suite de Fibonacci

Sur ma machine, la méthode récursive prend environ 22s (pour les 100 appels), alors que la méthode dynamique prend environ 1ms (pour les 100 appels). Vous devez retrouver des écarts comparables.
L'avantage est ici flagrant : un grand gain de temps pour une lisibilité du code un peu moins bonne.
La mémoïsation nécessite de stocker les résultats, on va donc avoir un encombrement de la mémoire qui peut devenir important sur des problèmes plus complexes.

Exercices

Optimisation de la découpe de planches

RésolutionS du problème

Dans l'arbre ci dessous, on retrouve sur chaque nœud la taille de la planche qu'il reste à découper et sur chaque lien la taille de la découpe. Si l'on prend la branche de gauche, en partant de la racine, on réalise tout d'abord une découpe de 1, il reste ensuite une planche de 3 à découper.
La découpe optimale d'une planche de 4 est donc "2-2" avec un gain de 10€.

Solution récursive

La longueur de la planche restante sera n-i.
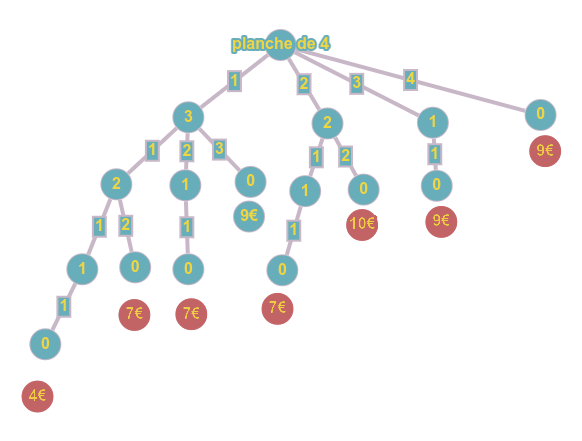
Le revenu optimal dans ce cas sera : p[i]+coupeRecurs(p, n-i)
Il faut choisir le maximum entre la découpe optimale d'une précédente hypothèse et la réponse à la question 2 : max(q,p[i]+coupeRecurs(p,n-i))

Implémentation :


def coupeRecurs(n, p):
    if n == 0:
        return 0
    else:
        q = -1
        for i in range (1, n+1):
            q = max(q, p[i]+coupeRecurs(n-i, p))
    return q

Solutions dynamiques

On retrouve dans cet arbre, deux fois la découpe d'une planche de longueur 2 :
Cette arbre a une taille de 16.
De façon plus générale, pour une planche de longueur n, l'arbre aura une taille de n²

Du haut vers le bas ou Top-Bottom

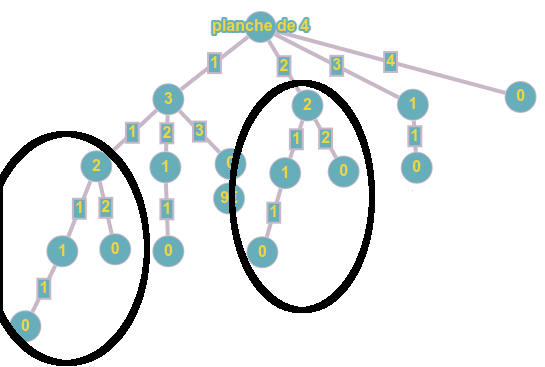
On reprend la structure à deux fonctions, la première permettant de créer le tableau de mémoïsation.


def plancheMemo(n, p):
    r = [None]*(n+1)
    return plancheMemoRecurs(n, p, r)
    						
def plancheMemoRecurs(n, p, r):
    if r[n]!=None:
        return r[n]
    elif n==0:
        r[n]=0
    else:
        for i in range(1, n+1):
            r[n]=max(r[n], p[i]+plancheMemoRecurs(n-i, p, r))
    return r[n]

Du bas vers le haut ou Bottom-Up


def plancheDynaBU(n, p):
    r = [0 for i in range(n+1)]
    for i in range (1, n+1):
        q = 0
        for j in range (1, i+1):
            q = max(q, p[j]+r[i-j])
        r[i] = q
    return r[n]

Le rendu de monnaie

Rappels : la résolution gloutonne

Si l'on applique la méthode gloutonne pour la somme de 1€77cts on obtient :
1€ + 50cts + 10cts + 10cts + 5cts + 2cts
Si l'on applique la méthode gloutonne pour la somme de 11cts on obtient :
0,10+????
La méthode gloutonne n'aboutit pas dans cette situation.
La solution pour 11cts est bien sur :
5cts + 2cts + 2cts + 2cts

Exploration exhaustive

Les branches ne terminant pas par 0 n'aboutissent pas.
Les branches terminant par 0 aboutissent.
La solution optimale ici est à 4 pièces (5+2+2+2).

						
print(renduRec(11, [100,50,10,5,2]))						
>>> 4

Pour les sommes 177cts et 289cts la fonction récursive aboutit après un temps trèèèèèèèèès long. La complexité temporelle n'est pas acceptable.

Approche dynamique

						
def rendu_dyna(somme, systeme):
    f=[-1]*(somme+1)
    return dyna_rendu_memo(somme, systeme, f)
    						
def dyna_rendu_memo(somme, systeme, f):
    if f[somme] != -1:
        return f[somme]

    if somme == 0:
        return 0

    else:
        mini = 1000
        for i in range(len(systeme)):
            if systeme[i] <= somme:
                nb = 1 + dyna_rendu_memo(somme-systeme[i], systeme, f)
                if nb < mini:
                    mini = nb
    f[somme] = mini
    
    return f[somme]

Complément : voila la version "bottom-up" ( donc itérative ) :

						
def dyna_rendu_memo_BU(somme, systeme):

    # ÉTAPE 1 : création et initialisation du tableau
    mem = [0]*(somme+1) 

    # ÉTAPE 2 : remplissage du reste du tableau par indice croissant
    for i in range(1, somme + 1) :
        for p in systeme :
            if p <= i:
                nb = 1 + mem[i-p]
                if nb < mem[i]:
                    mem[i] = nb

    # ÉTAPE 3 : le résultat est dans la dernière case
    return mem[somme]

Promenade dans un tableau de tableaux : projet Euler

Présentation du problème

					
def euler_recursif(m: list[list], i, j)->int:
    if i == 0 and j == 0:
        return m[i][j]
    elif i == 0:
        return m[i][j]+euler_recursif(m, i, j-1)
    elif j == 0:
        return m[i][j]+euler_recursif(m, i-1, j)
    else:
        return m[i][j]+min(euler_recursif(m, i-1, j), euler_recursif(m, i, j-1))
    
m = [[131, 673, 234],
    [201,96,342],
    [630,803,746]]
    
print(euler_recursif(m, 2, 2))

Résolution par programmation dynamique

Approche par mémoïsation

		
def euler_memo(m: list[list])->int:
    """Cette fonction crée le tableau de mémoïsation, appelle la fonction de calcul, 
    et renvoie le résultat"""    
    h = len(m)
    l = len(m[0])
    phi = [[-1 for j in range(l)] for i in range(h)]
    return euler_memo_calcul(m, h-1, l-1, phi)
    
def euler_memo_calcul(m: list[list], i: int, j: int, phi: list[list])->int:
    if phi[i][j] != -1:
        return phi[i][j]
        
    if i == 0 and j == 0:
        phi[i][j] = m[i][j]
    elif i == 0:
        phi[i][j] = m[i][j]+euler_memo_calcul(m, i, j-1, phi)
    elif j == 0:
        phi[i][j] = m[i][j]+euler_memo_calcul(m, i-1, j, phi)
    else:
        phi[i][j] = m[i][j]+min(euler_memo_calcul(m, i-1, j, phi), euler_memo_calcul(m, i, j-1, phi))
    
    return phi[i][j]
    
print(euler_memo(matrix))

Approche bottom-up


def euler_BU(m: list[list])->int:
    """Cette fonction crée le tableau, puis appelle la fonction de calcul, 
    et renvoie le résultat"""    
    h = len(m)
    l = len(m[0])
    phi = [[-1 for j in range(l)] for i in range(h)]
    return euler_BU_calcul(m, phi)
    
def euler_BU_calcul(m: list[list], phi: list[list])->int:
    for i in range(len(m)):
        for j in range(len(m[0])):
            if i == 0 and j == 0:
                phi[i][j] = m[i][j]
            elif i == 0:
                phi[i][j] = m[i][j] + phi[i][j-1]
            elif j == 0:
                phi[i][j] = m[i][j] + phi[i-1][j]
            else:
                phi[i][j] = m[i][j] + min(phi[i][j-1], phi[i-1][j])
    return phi[-1][-1]

Recherche du plus grand carré blanc

Présentation du problème

Identification du sous problème

Codage de la recherche du plus grand carré blanc

Fonction récursive

Si le pixel est noir il n'y a pas de carré blanc à cet emplacement, la fonction doit donc renvoyer 0.
Si x=0 ou y=0 on est au bord du carré à explorer, comme le pixel de coordonnées (x,y) correspond au coin en bas à droite, la fonction devra renvoyer 1 (à moins que le pixel soit noir...voir ci dessus).
Si le pixel de base a pour coordonnées (x,y), les trois carrés à tester ont pour coordonnées (x-1,y-1) (x,y-1) et (x-1,y)


m=1+min(plusGrdCarreBlancRecurs(x-1,y-1,img),plusGrdCarreBlancRecurs(x,y-1,img),plusGrdCarreBlancRecurs(x-1,y,img))


def plusGrdCarreBlancRecurs(x,y,img):
    if img[x][y]==1:
        return 0
    elif x==0 or y==0:
        return 1
    else:     m=1+min(plusGrdCarreBlancRecurs(x-1,y-1,img),plusGrdCarreBlancRecurs(x,y-1,img),plusGrdCarreBlancRecurs(x-1,y,img))
        return m

Pour tester cette fonction récursive, il faut tester tous les pixels de l'image :


max=0

for i in range (len(test[0])):
    for j in range (len(test[0])):
        print(i,j)
        if plusGrdCarreBlancRecurs(i,j,test) > max:
            max=plusGrdCarreBlancRecurs(i,j,test)

print('le max est ',max)

Fonction récursive avec mémoïsation : programmation dynamique de haut en bas


def plusGrdCarreBlancDyna1(x,y,img):
    memo=[[None]*len(img[0])]*len(img[0])
    return plusGrdCarreBlancMemo(x,y,img,memo)

def plusGrdCarreBlancMemo(x,y,img,memo):
    if memo[x][y]!=None:
        return memo[x][y]
    if img[x][y]==1:
        memo[x][y]=0
        return memo[x][y]
    elif x==0 or y==0:
        memo[x][y]=1
        return memo[x][y]
    else:
        memo[x][y] = 1+min(plusGrdCarreBlancMemo(x-1,y-1,img,memo),plusGrdCarreBlancMemo(x,y-1,img,memo),plusGrdCarreBlancMemo(x-1,y,img,memo))
        return memo[x][y]

Distance de Levenhstein

Analyse

pour un ajout/une insertion : d(i, j) = 1 + d(i, j-1)
pour une suppression : d(i, j) = 1 + d(i-1, j)
pour une lettre inchangée : d(i, j) = d(i-1, j-1)
pour une substitution : d(i, j) = 1 + d(i-1, j-1)

Le cas général sera de renvoyer le minimum parmi ces 4 distances possibles.

Les cas de base sont atteints lorsque :

soit la sous-chaîne i est vide ( i == - 1 ) : la distance par rapport à la sous-chaîne j est alors égale au nombre de caractères de cette dernière, soit j+1.
soit la sous-chaîne j est vide ( j == - 1 ) : on renvoie dans ce cas i+1.

Implémentation naïve


def dist_lev_rec(i, j):
    if i == -1:
        return j+1
    if j == -1:
        return i+1
    if ch1[i] == ch2[j]:
        cout_sub = dist_lev_rec(i-1, j-1)
    else:
        cout_sub = 1 + dist_lev_rec(i-1, j-1)
    cout_ajout = 1 + dist_lev_rec(i-1, j)
    cout_supp = 1 + dist_lev_rec(i, j-1)
    return min(cout_sub, cout_ajout, cout_supp)

On peut écrire plus succinctement :


def dist_lev_rec(i, j):
    if i == -1:
        return j+1
    if j == -1:
        return i+1
        
    cout = 0 if ch1[i] == ch2[î] else 1 # opérateur ternaire
    return min(1 + dist_lev_rec(i-1, j-1), 1 + dist_lev_rec(i, j-1), cout + dist_lev_rec(i-1, j-1))

Approche top-bottom ( avec mémoïsation )


def dist_lev_TB(i, j):
    if (i, j) in dist:
        return dist[(i, j)]
    if i == -1:
        return j+1
    if j == -1:
        return i+1
    if ch1[i] == ch2[j]:
        cout_sub = dist_lev_TB(i-1, j-1)
    else:
        cout_sub = 1 + dist_lev_TB(i-1, j-1)
    cout_ajout = 1 + dist_lev_TB(i-1, j)
    cout_supp = 1 + dist_lev_TB(i, j-1)
    cout_total = min(cout_sub, cout_ajout, cout_supp)
    dist[(i, j)] = cout_total
    return cout_total

dist est un dictionnaire initialement vide. Pour tester si une valeur a déjà été calculée auparavant, il suffit de déterminer si le couple (i, j) correspondant est déjà présent dans le dictionnaire ( complexité en O(1) ).

Approche bottom-up

On constate, pour i > 0 et j > 0, que la distance d(i, j) est le minimum entre :

1 + d(i-1, j),
1 + d(i, j-1),
d(i-1, j-1) si les caractères ch1[i-1] et ch2[j-1]sont identiques,
1 + d(i-1, j-1) sinon.

Par exemple :

Pour i = 2 et j = 4 ( distance entre 'CH' et 'CHUT' ) :

→ les lettres ( 'H' et 'T' ) sont différentes, donc : d(2, 4) = min(1+1, 1+2, 1+3) = min(2, 3, 4) = 2
Pour i = 4 et j = 4 ( distance entre 'CHAT' et 'CHUT' ) :

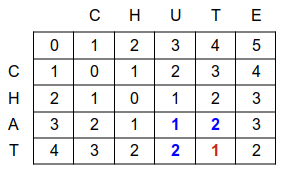
→ les lettres ( 'T' et 'T' ) sont identiques, donc : d(4, 4) = min(1+2, 0+1, 1+2) = min(3, 1, 3) = 1

La distance entre les deux chaînes ch1 et ch2 se trouve alors dans la case tout en bas à droite du tableau.


def dist_lev_BU(ch1, ch2):
    m = len(ch1)
    n = len(ch2)

    # Initialisation du tableau
    dp = [[0 for j in range(n+1)] for i in range(m+1)]

    # Remplissage de la première colonne et de la première ligne
    for i in range(m+1):
        dp[i][0] = i
    for j in range(n+1):
        dp[0][j] = j

    # Remplissage du tableau avec le calcul des distance pour chaque case (i, j) :
    for i in range(1, m+1):
        for j in range(1, n+1):
            if ch1[i-1] == ch2[j-1]:   # attention au décalage d'index : i = 0 ou j = 0 correspondent à une chaîne vide, pas au premier caractère des chaînes ( = indice 1 )
                d1 = dp[i - 1][j - 1]
            else:
                d1 = 1 + dp[i - 1][j - 1]
            d2 = 1 + dp[i-1][j]
            d3 = 1 + dp[i][j-1]
            dp[i][j] = min(d1, d2, d3)

    # Renvoi de la plus petite distance :
    return dp[m][n]  # ou dp[-1][-1]

-->