Correction : Piles

Implémentations des piles

Pile statique : implémentation avec tableau de taille fixe

L'idée : utiliser un attribut servant de "pointeur" désignant l'indice de l'élément du tableau constituant le sommet de la pile.

Cet attribut sera initialisé à -1 pour indiquer une pile vide, et incrémenté ( reps. décrémenté ) AVANT chaque empilage ( resp. dépilage ).
On peut aussi faire le choix de l'initialiser à 0 pour une pile vide, et faire l'incrémentation/décrémentation APRÈS chaque empilage/dépilage, mais dans ce cas, l'élément "pointé" par l'attribut sommet ne représente plus le sommet de la pile, mais "l'élément immédiatement au dessus du sommet"...

class PileStat:

    def __init__(self,n):
        self.sommet = -1                 # indice du sommet dans le tableau ( initialement, "avant" le premier élément du tableau )
        self.pile = [None]*n             

    def est_vide(self):
        return self.sommet == -1

    def empiler(self, elt):
        assert self.sommet < len(self.pile), "Stack overflow ( la pile est pleine )"
        self.sommet += 1                # on incrémente le pointeur de sommet
        self.pile[self.sommet] = elt    # on place l'élément au sommet
        
    def depiler(self):
        assert not self.est_vide(), "Stack underflow ( la pile est vide )"
        s = self.pile[self.sommet]      # "sauvegarde" de l'élément au sommet de la pile
        self.pile[self.sommet] = None   # on "efface" l'élément au sommet
        self.sommet -= 1                # on décrémente le pointeur de sommet
        return s                        # on renvoie l'élément à l'ancien sommet
			

On retrouve bien ici les concepts de la POO : ce qui représente la pile elle-même est l'objet self; le tableau Python utilisé n'est qu'un attribut de cet objet, le reste de la classe étant ses méthodes.

Tests à réaliser :

• instancier un objet pile de 10 éléments :

  
  pile = PileStat(10)				
  					

• empiler/dépiler quelques éléments :

  
  pile.empiler(12)
  pile.empiler(25)
  pile.empiler(36)
  print(pile.depiler())		
  					

• remplir la pile, et vérifier qu'elle ne déborde pas :

  
  for i in range(9): # pour i = 11, la pile devrait déborder
  	pile.empiler(i)						
  					

• dépiler la pile, jusqu'à avoir une pile vide :

  
  while not pile.est_vide():
  	print(pile.depiler())						
  					

Pile dynamique : implémentation avec tableau dynamique

Trop facile 😊 :

class PileDyna:

    def __init__(self):
        self.pile = []

    def est_vide(self):
        return len(self.pile) == 0 # ou self.pile == []

    def empiler(self, elt):
        self.pile.append(elt)      # pas de précondition sur cette méthode, cette pile ne peut jamais être pleine !!

    def depiler(self):
        assert not self.est_vide(), "Stack underflow ( la pile est vide )"
        return self.pile.pop()
			

La méthode Python pop renvoie l'élément supprimé en fin de tableau, on peut donc l'utiliser directement après le return.

Comparaison des implémentations

1. Tableau de taille fixe :

• accès direct à l'élément au sommet de la pile, donc empilage et dépilage en O(1)
• adaptable à n'importe quel langage
• taille réduite en mémoire
• ...mais donc capacité limitée !

2. Tableau dynamique ( type list Python ) :

• opération append et pop en O(1), mais c'est du "pseudo" O(1) ( cf. chapitre sur les listes ).
• capacité extensible à l'infini !
• encombrement inutile de la mémoire pour de petites piles.

3. Autre implémentation judicieuse :

Une implémentation par liste chaînée, avec le sommet de la pile en tête de liste, permet d’avoir des opérations de dépilage et d'empilage en "vrai" O(1).

Pile optimisée : implémentation avec une liste chaînée

Il s'agit du code de la pile dynamique, mais en utilisant un objet de type Liste pour implémenter la pile, et en remplaçant les méthodes append et pop respectivement par les méthodes insert_first et pop_first de la liste chaînée :

from liste_chainee import Liste

class PileOptim:

    def __init__(self):
        self.pile = Liste()          # une pile vide est une Liste vide

    def est_vide(self):
        return self.pile.is_empty()

    def empiler(self, elt):
        self.pile.insert_first(elt)

    def depiler(self):
        assert not self.est_vide(), "Stack underflow ( la pile est vide )"
        return self.pile.pop_first()
            

Mais plutôt que d'importer le module liste_chainee en totalité, alors que l'on ne va finalement utiliser que très peu de ses méthodes, il est quand même plus judicieux de recoder complètement les méthodes de piles; dans ce cas, on n'importe que la classe Maillon :

from liste_chainee import Maillon

class PileOptim:

    def __init__(self):
        self.sommet = None          # une pile vide n'a pas de maillon au sommet

    def est_vide(self):
        return self.sommet is None

    def empiler(self, elt):
        self.sommet = Maillon(elt, self.sommet)

    def depiler(self):
        assert not self.est_vide(), "Stack underflow ( la pile est vide )"
        elt = self.sommet.valeur
        self.sommet = self.sommet.suivant
        return elt

    def __str__(self):
        result = '\n'
        maillon = self.sommet
        while maillon is not None:
            result += "| " + str(maillon.valeur) + " | \n"
            maillon = maillon.suivant
        return result + "------ \n "
            

Code complet

Le code complet des 3 classes est dans le fichier : pile.py.

La classe Maillon est directement intégrée dans le fichier, inutile donc d'importer aussi le fichier liste_chainee.py.

Exercices sur les piles

Inversion d'une pile

Oui, il faudra une deuxième pile : en "vidant" complètement la première dans la deuxième, et en renvoyant cette deuxième, on a bien renversé la première...

Pour ne pas modifier la pile d'origine, il en faudra également une troisième pour stocker temporairement les éléments dépilés de la première pile, de façon en fin de fonction à pouvoir y ré-empiler ses éléments :

from pile import *
			
def inversion_pile(pile):
	p_inv = Pile()	# pile inversée
	p_temp = Pile()	# pile temporaire

	while not pile.est_vide():# tant que la pile d'origine n'est pas vide,
		elt = pile.depiler()  # on dépile son sommet,
		p_inv.empiler(elt)    # et on stocke ce sommet dans p_inv
		p_temp.empiler(elt)   # et dans p_temp.
	
	while not p_temp.est_vide():
		pile.empiler(p_temp.depiler()) # on ré-empile tous ses éléments sauvegardés dans la pile d'origine

	return p_inv # et on ne renvoie que la pile inversée !
			

Inversion d'une chaîne

L'idée :

• on empile tous les caractères de la chaîne dans une pile initialement vide, créé à cet effet dans la fonction
• on les dépile les uns après les autres, et on les concatène à une nouvelle chaîne, jusqu'à avoir "vidé" la pile.

	
from pile import *
		
def inversion_chaine(ch: str)->str :
    pile = Pile() # création de la pile

    for car in ch: # empilage des caractères de la chaîne
        pile.empiler(car)

    c2 = '' # nouvelle chaîne
    
    while not pile.est_vide():  # tant que la pile n'est pas vide,
        c2 = c2 + pile.depiler()# on dépile chaque caractère et on le concatène à la nouvelle chaîne.

    return c2
			

Remarque :

Vous avez déjà fait cet exercice avec une fonction récursive, et on avait alors parlé à ce moment de "pile d'exécution".

L'exécution des fonctions récursives fait effectivement appel à la structure de données PILE que vous venez d'étudier, pour stocker les résultats intermédiaires et les résultats à renvoyer.

Vous pourriez d'ailleurs refaire tous les exercices du chapitre Récursivité, mais en écrivant un code itératif utilisant une pile !

Maximum/minimum dans une pile

Vous connaissez bien entendu l'algorithme de recherche d'un maximum/d'un minimum dans un tableau : il faut parcourir le tableau, et comparer chacun de ses éléments au maximum/au minimum "courant" stocké dans une variables.

Ici, le TAD PILE ne permet pas un parcours de la structure, il faut donc s'arranger avec le fait que l'on n'a accès qu'à son sommet...

L'idée :

• on dépile les éléments les uns après les autres
• on compare chaque élément à une variable maximum ou minimum, et on modifie la valeur de cette dernière au besoin
• après dépilage complet, on ré-empile tous les éléments de la pile que l'on avait pris soin de sauvegarder dans une autre pile.

from pile import *

def maximum_pile(pile)->int:
    p_temp = Pile()
    maximum = pile.depiler() # maximum initialisé au premier élément de la pile
    p_temp.empiler(maximum)  # à empiler tout de suite dans la pile temporaire de sauvegarde
    
    while not pile.est_vide():
        elt = pile.depiler()
        if elt > maximum:
            maximum = elt
        p_temp.empiler(elt)
        
    while not p_temp.est_vide():
        pile.empiler(p_temp.depiler())
        
    return maximum



def minimum_pile(pile)->int:
    p_temp = Pile()
    minimum = pile.depiler()
    p_temp.empiler(minimum) 
    
    while not pile.est_vide():
        elt = pile.depiler()
        if elt < minimum:
            minimum = elt
        p_temp.empiler(elt)
        
    while not p_temp.est_vide():
        pile.empiler(p_temp.depiler())
        
    return minimum
			

Copie d'une pile

Il faut ici deux piles supplémentaires :

• l'une qui constituera la copie de la pile d'origine
• l'autre qui permettra de dépiler les éléments de la pile d'origine, puis de ré-empiler tous ces éléments dans la pile d'origine ET dans la copie

from pile import *

def copie_pile(pile):
    p_temp = Pile()
    p_copie = Pile()
    
    while not pile.est_vide():
        p_temp.empiler(pile.depiler())   
        
    while not p_temp.est_vide():
        elt = p_temp.depiler()
        pile.empiler(elt)
        p_copie.empiler(elt)
        
    return p_copie
    		

Simulation de la récursion avec une pile

Somme des entiers de 1 à N

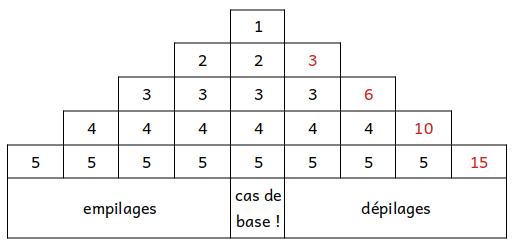
from pile import *

def sum_stack(n):
    s = Pile()
    while n != 0:
        s.empiler(n)
        n -= 1
        print(s)

    while not s.est_vide():
        try:
            resultat = s.depiler() + s.depiler()
            s.empiler(resultat)
            print(s)
        except:
            pass
    return resultat


print(somme(10)) # renvoie 55		
			

Factorielle

On change l'opération effectuée lors du dépilage des données :

from pile import *

def fact(n):
    s = Pile()
    while n != 0:
        s.empiler(n)
        n -= 1
        print(s)

    while not s.est_vide():
        try:
            resultat = s.depiler() * s.depiler()
            s.empiler(resultat)
            print(s)
        except:
            pass
    return resultat

print(fact(10)) # renvoie 3628800		
			

Somme des éléments d'un tableau

from pile import *

def somme(L):
    s = Pile
    n = 0
    while n != len(L):
        s.empiler(L[n])
        n += 1
        print(s)

    while not s.est_vide():
        try:
            resultat = s.depiler() + s.depiler()
            s.empiler(resultat)
            print(s)
        except:
            pass
    return resultat			
			

Vérification du parenthésage

Algorithme à suivre

• on parcourt chaque caractère de la chaîne représentant l'expression;
• si le caractère courant est un symbole "ouvrant" :
  • on l'empile
• si ce caractère est un "fermant" :
  • on teste si la pile est vide : si oui, cela signifie une erreur, on termine en renvoyant False
  • si elle n'est pas vide :
    • on dépile le sommet de la pile,
    • et on vérifie si le caractère "ouvrant" dépilé correspond bien au "fermant" courant : si ce n'est pas le cas, on termine en renvoyant False.
• en fin de parcours, on vérifie si la pile est bien vide :
  • si ce n'est pas le cas, il reste des "ouvrants" non "appariés", donc on termine en renvoyant False
  • sinon, tous les symboles correspondent, on renvoie donc True.

Implémentation

1^ère méthode

L'ensemble des caractères ouvrants et fermants sont stockés dans 2 chaînes de caractères, dans le même ordre : pour savoir si un élément de l'expression est un caractère ouvrant ou fermant, on regarde alors simplement si il est dans l'une ou l'autre de ces chaînes.

Pour savoir si un caractère ouvrant est correctement "apparié" à son ouvrant, on compare alors la position ( indice ) de l'ouvrant et du fermant dans leur chaîne respective ( méthode de chaîne index, qui renvoie l'indice d'un élément donné dans une chaîne ): si ces indices sont les mêmes, l'ouvrant et le fermant correspondent.

from pile import *

def check_parenth(exp: str)->bool:
    pile = Pile()
    ouvrants ='{(['  # chaîne contenant les caractères ouvrant, 
    fermants = '})]' # et chaîne contenant les caractères fermants, DANS LE MÊME ORDRE
    
    for car in exp :                                          # pour chaque caractère 'car' de la chaîne,
        if car in ouvrants:                                   # si 'car' est un ouvrant,
            pile.empiler(car)                                 # on l'empile.
        if car in fermants:                                   # si 'car' est un fermant,
            if pile.est_vide() :                              # on teste tout d'abord si la pile n'est vide;
                return False                                  # si c'est le cas, cela signifie qu'il y avait "trop" de fermants par rapport aux ouvrants, on signale l'erreur.
            f = pile.depiler()                                # sinon, on dépile le dernier ouvrant,                           
            if ouvrants.index(f) != fermants.index(car):      # et on le compare au fermant courant;
                return False                                  # si les deux ne coïncident pas, on signale l'erreur.
            
    return pile.est_vide()                                    # en fin de parcours, si la pile n'est pas vide, cela indique qu'il y avait trop d'ouvrants par rapport aux fermants.
			

2^ème méthode

Une structure plus judicieuse est un dictionnaire, dans lequel les ouvrants sont les clés, et les fermants correspondant, les valeurs (ou l'inverse).

Pour tester si un ouvrant et un fermant sont correctement "appariés", on teste alors si la valeur (un fermant) est associée à la "bonnes" clé (un ouvrant).

def check_par_v2(exp: str)->bool:
    pile = Pile()
    symboles = {"(": ")", "[": "]", "{": "}"}   # dictionnaire {ouvrant: fermant associé}

    for car in exp :
        if car in symboles.keys():            # les ouvrants sont les CLES du dictionnaire
            pile.empiler(car)
        if car in symboles.values():              # les fermants en sont les VALEURS
            if pile.est_vide() :
                return False
            f = pile.depiler()
            if symboles[f] != car:              # si la valeur dans le dictionnaire associée à la clé 'f' n'est pas égale au fermant courant 'car',
                return False                    # alors erreur.

    return pile.est_vide()                               
			

Ouverture à d'autres langages : Forth

Calculs en RPN

Manipulation des piles : tri d'une pile

"Fonctions" en Forth

Structures de contrôle

Conditions

Boucles