Correction : principes de la récursivité

La fonction mystère

def f(a, n):
	if n == 0:
		return 0 
	return a + f(a, n-1)
			

Cas de base : lignes 3 et 4

Cas général : ligne 5

La fonction prend 2 paramètres, a et n. Le premier n'est jamais modifié, le deuxième diminue de 1 à chaque appel récursif.

→ exemple pour a = 2 et n = 3 :

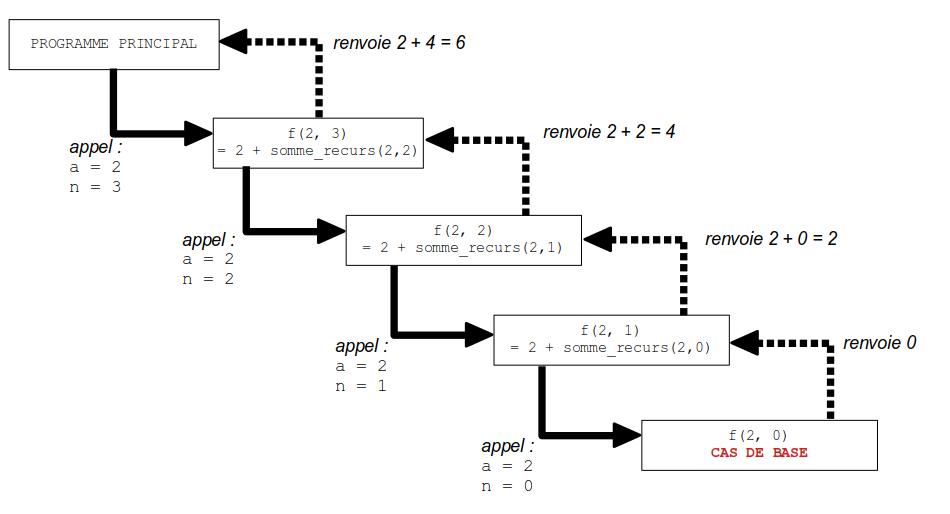
→ la fonction fait donc le produit de a par n.

Fonction puissance

Version itérative

def puissance(y:int, x: int)->int:
	p = 1
	for i in range(x):
		p = p * y
	return p
			

Version récursive

Cas général

Prenons l'exemple de x = 4 ( et y n'importe quelle valeur ) :

• y⁴ = y * y * y * y = y * y³ soit : puissance(y, 4) = y * puissance(y, 3)
• y³ = y * y * y = y * y² soit : puissance(y, 3) = y * puissance(y, 2)
• y² = y * y = y * y¹ soit : puissance(y, 2) = y * puissance(y, 1)
• y¹ = y * 1 = y * y⁰ soit : puissance(y, 1) = y * puissance(y, 0)
• y⁰ = 1 : Cas de base !

Donc : y^x = y * y^x-1, soit : puissance(y, x) = y * puissance(y, x - 1)

Cas de base

On arrête la récursion quand x == 0, et on renvoie alors 1.

(Remarque : pour "économiser" un appel récursif, on peut aussi prendre comme cas de base : quand x == 1, renvoyer y...)

Fonction complète

def puis_recurs(y: int, x: int)->int:
	if x == 0 : 
		return 1
	else:
		return y * puis_recurs(y, x-1)
			

Construire une chaîne

Cas général

Prenons par exemple i = 1 et n = 5 : la chaîne renvoyée par la fonction devra donc être "12345"

• '12345' = '1' + "2345" soit : chaine(1, 5) = '1' + chaine(2, 5)
• '2345' = '2' + "345" soit : chaine(2, 5) = '2' + chaine(3, 5)
• '345' = '3' + "45" soit : chaine(3, 5) = '3' + chaine(4, 5)
• '45' = '4' + "5" soit : chaine(4, 5) = '4' + chaine(5, 5)
• '5' = '5', plus rien à concaténer : Cas de base !

On en déduit donc que pour toute valeur de i : chaine(i, n) = i + chaine(i+1, n)

Cas de base

Quand i == n, on renvoie le dernier nombre à concaténer, à savoir n ( ou i, ils sont alors égaux 😏 )

Fonction complète

def chaine(i: int, n: int)->str:
	if i == n:
		return str(i)  # attention au transtypage indispensable int -> str !
	else:
		return str(i) + chaine(i+1, n)	
			

Caractère dans une chaîne

Cas général :

Ici, il faut voir que l'on va se contenter de "parcourir" la chaîne caractère après caractère depuis le premier : pour cela, on appelle la fonction en lui passant comme paramètre à chaque appel récursif, la chaîne, le caractère à rechercher et un troisième paramètre servant de "pointeur d'index" qui sera incrémenté à chaque appel récursif ( ceci jouant donc le rôle d'une itération du type : for caractere in chaine ).

Un caractère se trouve dans la chaîne, si il est à l'indice n OU dans la suite de la chaîne, donc :

est_dans(n) = chaine[n] == car or est_dans(n+1)

Cas de base :

On parcourt la chaîne caractère après caractère; en arrivant au dernier caractère, on renvoie simplement le résultat de l'expression booléenne chaine[n] == car, qui évalue si le dernier caractère est celui recherché; plus besoin alors d'appel récursif...

→ fonction complète :

	
def est_dans(ch: str, car: str, n = 0)->bool:         # n = index du caractère "en cours", initialisé à 0 par défaut
    if n == len(ch)-1:                                # cas de base : on est arrivé au dernier caractère ( attention à l'indice de celui-ci ! )
        return ch[n] == car                           # le dernier caractère est celui recherché ?
    else:
        return est_dans(ch ,car, n+1) or ch[n] == car # cas général : appel récursif en incrémentant 'n' de 1 à chaque appel
        

	
........
    else:
        est_dans(ch ,car, n+1) or ch[n] == car # pas de 'return'...
        		

Remarque importante