Favicon

NSI Vaugelas - Terminale

Connexion

Sommaire

Correction : exercices récursivité

Compte à rebours

Version descendante :

Cas de base : n = 0 → renvoi de 'Ignition !'

Cas général : simple appel récursif de la fonction avec n-1 comme argument


def rebours(n):
    if n == 0:
        return 'Ignition !'
    else:
        print(n)
        return rebours(n-1)
    
print(rebours(10)) # appel de la fonction et affichage du résultat renvoyé

Une version plus jolie...

A noter que l'on est obligé d'inclure une instruction print() dans la fonction ce qui n'est pas une bonne pratique : le seul résultat à afficher devrait être celui renvoyée par la fonction au programme principal, mais il faut cependant ici afficher le décompte à chaque appel récursif.

Au lieu d'afficher, on peut donc plutôt construire une chaîne constituée des différents résultats des appels récursifs successifs :


def rebours(n):
    if n == 0:
        return 'Ignition !'
    else:
        return str(n) + "\n" + rebours(n-1)
    
print(rebours(10)) # appel de la fonction et affichage du résultat renvoyé

Le caractère d'échappement "\n" permet de faire un retour à la ligne dans une chaîne de caractères.

Version ascendante :

Il faut effectivement utiliser ici 2 paramètres pour la fonction :


def rebours(n, i = 0): # n = paramètre fixe ( limite haute du compte à rebours ) / i = paramètre variable ( croissant de 0 à n )
    if n == i:
        return 'Ignition !' # cas de base quand n == i : limite atteinte
    else:
        return str(i) + "\n" + rebours(n, i+1) # appel récursif en augmentant la valeur de i
    
print(rebours(10)) # appel de la fonction avec seulement la valeur de n renseignée : i prend la valeur 0 par défaut

Fonction factorielle

Version itérative


def factorielle(n):
    fact = 1
    for i in range(1,n+1):
        fact = fact*i
    return fact

Version récursive

Cas général : on peut tester sur un exemple ( n = 4 ) pour déterminer l'expression générale :

Cas de base : on arrête la récursion quand n = 1, et on renvoie alors 1 ( ou n, c'est alors la même chose...).

→ fonction complète :


def factorielle_recurs(n):
    if n == 1:
        return n
    else:
        return n*factorielle_recurs(n-1)

Construction d'un tableau

1ère possibilité : on ajoute des éléments de tableau...

Attention à la manière d'ajouter un élément à un tableau : tab = tab + [valeur]; il faut ajouter à la fin d'un tableau bien un élément de tableau ( d'où les crochets [a] ), et pas seulement la valeur de cet élément ( a, ce qui donnerait une erreur de type...) !


def construction_tableau(a: int, b: int)->list:

	if a == b:
		return [a] # ou [b]
	else:
		return [a] + construction_tableau(a+1, b) # le paramètre b ne change jamais

2ème méthode plus efficace : on append des éléments...

La méthode append des tableaux est plus efficace que "l'ajout' d'élément à la fin d'un tableau ( nous verrons pourquoi plus tard ).

On peut donc remplacer cet ajout par un append à la fin d'un tableau, initialement vide, et passé en paramètre à chaque appel récursif :


def construction_tableau(a: int, b: int, tab: list)->list:
	if a == b:
	    tab.append(a)
	else:
	    tab.append(a)
	    construction_tableau(a+1, b, tab) # simple appel récursif, la fonction ne renvoie rien...
	return tab 				# le renvoi du tableau complet se fait en fait ici !

print(construction_tableau(2, 15, [])) # nécessité de passer un 3ème argument à l'appel initial

On pourrait être tenté, pour simplifier l'appel de la fonction, de donner au paramètre tab une valeur par défaut ( le tableau vide ici ) :


def construction_tableau(a, b, tab = []): # au premier appel, 'tab' est un tableau vide
	if a == b:
	    ...

Mais c'est à proscrire : pour des raisons qui sont expliquées ici, il ne faut JAMAIS utiliser un type mutable ( listes, dictionnaires ) comme valeur par défaut d'un paramètre dans une fonction.

Attention, la méthode append ne renvoie rien, il ne faut donc surtout pas écrire des choses comme :


		...
		return tab.append(a)  # renvoie None !!

Élément dans un tableau

Version naïve...

Tout à fait similaire à la recherche d'un caractère dans une chaîne ( exercices du chapitre ), adapté à un tableau 😎 :

	
def est_dans(tab: list, elt: int, n = 0)->bool: # n = index de l'élément "en cours", initialisé à 0 par défaut
    if n == len(tab): # cas de base : on est arrivé en bout de tableau -> élément pas trouvé
        return False
    if tab[n] == elt: # cas de base : élément d'indice n dans le tableau == élément recherché -> élément trouvé
        return True
    else:
        return est_dans(tab ,elt, n+1) # appel récursif en incrémentant n de 1 à chaque appel

Version plus subtile...

On peut "penser plus récursif" :

D'où la fonction :


def est_dans(tab: list, elt: int, n = 0)->bool:     # n = index de l'élément "en cours", initialisé à 0 par défaut
    if n == len(tab)-1:                             # cas de base : on est arrivé au dernier élément du tableau
        return tab[n] == elt
    return tab[n] == elt or est_dans(tab ,elt, n+1) # cas général

Deux situations peuvent alors se présenter :

Gros inconvénient : cette approche nécessite de parcourir le tableau en entier jusqu'à son dernier élément, alors que la version précédente permettait d'arrêter la récursion lorsque l'on trouvait la valeur à un indice donnée.
En effet, le cas de base n'est vérifié que lorsque l'indice n est égal à celui du dernier élément du tableau...

Utiliser le module recviz pour bien visualiser ces "remontées" depuis le cas de base...

Parité d'un nombre

En appliquant simplement le principe proposé :

	
def est_pair(n :int)->bool:
	if n == 0:
		return True
	else:
		return not est_pair(n-1)

Il fallait ici comprendre "l'opposé de la parité" comme une négation logique d'un booléen True ou False ( résultat renvoyé par la fonction ), correspondant à l'opérateur not.

Somme des éléments d'un tableau

Cas général : somme(tableau) = premier élément du tableau + somme(reste du tableau)

Cas de base : si on arrive au dernier élément du tableau, alors on renvoie simplement cet élément.

L'idée est là aussi d'utiliser un paramètre supplémentaire destiné à parcourir les éléments du tableau; ce paramètre donnera l'indice du "premier élément du tableau", comme si ce dernier se "raccourcissait" d'un élément à chaque récursion :


def somme_recurs(L, n = 0):                # n = indice du début du 'reste du tableau', initialisé par défaut à 0
    if n == len(L)-1:                      # si on arrive au dernier élément du tableau
        return L[n]	                       # alors on renvoie simplement la valeur de cet élément.
    else :
        return L[n] + somme_recurs(L, n+1) # incrémentation du paramètre : on parcourt le tableau élément après élément

L = [12, 45, 2, 23, 7, 8 ,1]
print(somme_recurs(L))

>>> 98

Somme des chiffres d'un nombre


def somme_chiffres(N): 
    if N < 10:								# si N n'est constitué que d'un seul chiffre,
    	return N							# alors on retourne N et le calcul est terminé ( cas de base )
    else:
    	return N%10 + somme_chiffres(N//10) # calcul de : chiffre le plus à droite + somme(reste des chiffres)

Miroir

Cas général

Attention, moins évident : travailler sur un exemple "papier" est indispensable pour trouver le "lien" entre les niveaux de récursion !

Prenons l'exemple de la chaîne 'salut' à inverser; on doit donc obtenir 'tulas'

Donc, pour un caractère quelconque, on a : miroir(chaine) = miroir(reste de la chaîne) + le caractère, en partant du principe que l'on va parcourir la chaîne de la gauche vers la droite ( on aurait pu faire l'inverse aussi...)

On va là aussi se servir d'un paramètre supplémentaire pour parcourir la chaîne; pour un caractère d'indice n dans la chaîne, on aura alors : miroir(ch, n) = miroir(ch, n+1) + ch[n]

Cas de base

On parcourt la chaîne caractère après caractère; la récursion doit donc s'arrêter quand on arrive au dernier caractère de la chaîne; à ce moment, on renvoie seulement ce caractère.

Fonction complète


def miroir(ch: str, n = 0)->str :
    if n == len(ch)-1 : # dernier caractère ?
        return ch[n]	# on renvoie seulement ce caractère
    else:
        return miroir(ch, n+1) + ch[n]

Tableau trié ?

Il y a plusieurs façons de traiter ce problème, en voici deux.

Version "parcours bête et méchant"

Cas général : on parcourt le tableau élément après élément ( simple appel récursif ).

Cas de base : au nombre de deux :


def est_trie(T, n = 0):
    if n == len(T)-1: # attention à l'indice du dernier élément du tableau !
        return True
    elif T[n] > T[n+1]:
        return False
    else:
    	return est_trie(T, n+1)	
    	
print(est_trie(T1))
print(est_trie(T2))

>>> False
>>> True

Remarque importante : on peut être tenté, dans une situation comme celle-ci où le cas général ne fait qu'un simple appel récursif sans qu'il y ait de calcul, à écrire quelque chose comme :


def est_trie(L, n = 0):
    if n == len(L)-1:
        return True
    elif L[n] > L[n+1]:
        return False
    else:
    	est_trie(L, n+1) # pas besoin du return, un simple appel devrait suffire...

→ problème : la fonction renvoie dans tous les cas None, c'est à dire "Rien" !

Faisons le tracé des appels/renvoi sur un exemple simple pour comprendre l'origine du problème :

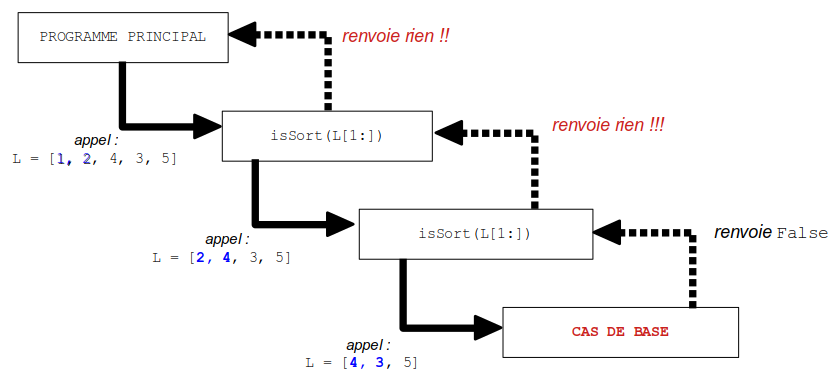
Trace récursion liste triée problème None

→ il y a bien un renvoi de résultat au niveau "le plus bas" de la récursion ( lorsque le cas de base est vérifié ), mais ensuite plus aucun résultat ne "remonte" vers les niveaux supérieurs : il ne faut surtout pas croire que le return du cas de base fait complètement sortir de la récursion, il termine simplement un des appels et le programme revient seulement au niveau supérieur : si celui-ci ne renvoie alors rien, le "False" a été "perdu" !

Aucun résultat n'est donc finalement renvoyé au programme principal, d'où l'affichage de None.( vous pouvez aussi essayer avec l'exercice 2.1, c'est la même conséquence...)

Il faut toujours avoir à l'esprit qu'il y a plusieurs niveaux de récursion, et qu'il y a donc toujours une phase de retour des appels récursifs : ne jamais oublier le return même si on pense ( à tort ) qu’aucun résultat de calcul n'est nécessaire d'être "remonté".

Version plus subtile...

On peut aussi voir les choses sous cet angle :

D'où la fonction :


def est_trie(T: list, n=0)->bool:
    if n == len(T)-1: # cas de base
        return True
    else:
        return T[n+1] >= T[n] and est_trie(T, n+1) # cas général

Si à un indice n donné, on rencontre une situation pour laquelle T[n+1] < T[n], la condition dans le cas général est alors évaluée à False, ce qui, d'après les propriétés de l'opérateur logique AND, fait "remonter" ensuite ce False jusqu'au premier appel de la fonction.

Contrairement à l'exercice est_dans, ce n'est pas ici un inconvénient de parcourir le tableau jusqu'à son dernier élément, il faut le faire de toute façon !

Conversion décimal → binaire

Méthode par soustraction

Cas général

Au nombre de deux :

Cas de base

Si on a traité la puissance 0 de 2, alors on renvoie 'chaîne vide'.


def binaire(d: int, n: int)->str :
	"""
	Entrées:
		d = entier en base 10 à convertir
		n = puissance de 2 ( au début = nombre de bits - 1 )
	
	Sortie :
		une chaîne de caractères représentant le nombre binaire
	"""
	
	if n < 0:
		return ''
	else :
		if (d - 2**n >= 0):
			return "1" + binaire(d-2**n, n-1)
		else:
			return "0" + binaire(d, n-1)

Méthode par division


def binaire(N):
    if N == 0:
        return ''
    else :
    	return binaire(N//2) + str(N % 2)

Facile, non ? :-))

Chiffres romains

Cas général

Au nombre de deux :

Cas de base

Si on arrive au dernier chiffre du nombre romain, on renvoie simplement son équivalent en base 10.


def rom2dec(rom, n = 0):
    if n == len(rom)-1: # attention à l'indice du 'dernier chiffre du nombre romain' !
        return equi[rom[n]] # et attention à la manière d'adresser une valeur dans un dictionnaire grâce à sa clé...
    else:
	    if equi[rom[n]] >= equi[rom[n+1]]: # on compare bien les valeurs associées aux clés, pas les clés elle-mêmes !
	        return equi[rom[n]] + rom2dec(rom, n+1)
	    else :
	       return rom2dec(rom, n+1) - equi[rom[n]]

equi = {'M':1000, 'D':500, 'C':100, 'L':50, 'X':10, 'V':5, 'I':1 } # dictionnaire des équivalences chiffres romains <-> base 10	
print(rom2dec('MCMLXXI'))

>>> 1971

Algorithmes de tri

Tri par sélection

Rappel de l'algorithme

La traduction "littérale" de l'algorithme est la suivante :


				pour chaque élément du tableau :
					pour chaque élément du reste du tableau :
						trouver l'élément minimum
					fin pour
					échanger l'élément et l'élément minimum
				fin pour

En plus détaillé ( "pseudo-code" ) :


				fonction tri_selection :
					entrée : un tableau T
					sortie : le même tableau, trié
					
					pour i variant de 0 à N - 1 : ( N = nombre d'éléments dans le tableau )
						m <- i 						
						pour j variant de i+1 à N - 1:
							si T[j] < T[m]:
								m <- j
							fin si
						fin pour
						échanger T[i] et T[m]
					fin pour
					renvoyer T

La "recherche du minimum dans le reste du tableau" correspond aux lignes 7 à 12.

Complexité

Elle va logiquement s'exprimer en fonction de N, nombre d'éléments dans le tableau.

Explication détaillée mais pas au programme, uniquement pour les matheux curieux...

Si l’on veut savoir plus précisément combien de fois la boucle interne est exécutée, il est possible de le calculer directement : à chaque itération de la boucle i , la boucle j "tourne" N-1 fois, puis N-2 fois, puis N-3, etc. jusqu'à 1, soit un nombre total de : (N-1)+(N-2)+(N-3)+....+1.
Mathématiquement, on sait que cette somme est égale à : N(N-1)/2 ce qui donne un polynôme en N² : cette analyse est plus précise mais ne change donc pas la complexité qui reste en O(N²).

Version itérative


def tri_selection(T):
    for i in range(len(T)): 		# pour chaque élément du tableau
        m = i 						# index de l'élément minimum, initialisé à i
        for j in range(i+1,len(T)): # parcours du 'reste du tableau'
            if T[j] < T[m]: 		# a-t-on trouvé un élément plus petit ?
                m = j 				# si oui, alors c'est notre minimum ( pour l'instant...)
        T[i], T[m] = T[m], T[i] 	# échange des deux éléments ( attention, spécificité Python ! )
        
    return T

Le tri par sélection est un tri "en place", car le tableau est directement trié sans qu'il soit nécessaire d'en créer un autre.

Version récursive

L'idée est d'utiliser la récursion pour qu'elle remplace la boucle de parcours du tableau ( boucle i dans le script ).

On va utiliser le fait que le début du tableau est forcément trié, puisqu'on vient y placer au fur et à mesure les éléments par ordre croissant :


def tri_selection(T, i = 0):
    if i == len(T)-1: # cas de base
        return [T[i]]
    else:
        m = i 						
        for j in range(i+1,len(T)): # recherche du minimum dans le reste du tableau
            if T[j] < T[m]: 		
                m = j 				
        T[i], T[m] = T[m], T[i] # échange avec l'élément courant 	

    return [T[i]] + tri_selection(T, i+1) # cas général

Remarque : avec le module recviz, on constate que le tri commence ici par la fin du tableau.

Tri par insertion

Rappel de l'algorithme

La traduction "littérale" de l'algorithme est la suivante :


				pour chaque élément du tableau :
					venir le placer à sa "bonne" place dans le début du tableau ( qui est trié )
				fin pour

Pour "placer l'élément i à sa bonne place", l'idée est de parcourir le début trié du tableau ( soit de l'indice 0 à l'indice i-1 ), de rechercher la "bonne" place, de décaler vers la droite tous les éléments suivants pour "faire de la place", et d'insérer alors l'élément dans le "trou" ainsi créé.

Dans la pratique, pour trouver la "bonne" place, on va parcourir la partie triée du tableau du haut vers le bas ( donc de i-1 à 0 ), en décalant vers la droite les éléments triés tant que l'élément à placer est plus grand que les éléments en place : quand ce n'est plus le cas, on a trouvé la "bonne" place de l'élément, et on l'insère alors.

Ce mode de fonctionnement impose que l'on garde "en mémoire" l'élément à placer car il va se faire "écraser" par ces décalages vers la droite : 


				fonction tri_insertion :
					entrée : un tableau T
					sortie : le tableau T, trié ( c'est donc aussi un algorithme de tri en place...)
					
					pour i variant de 0 à N :
						temp <- T[i] ( on garde en mémoire l'élément à placer )
						j <- i-1 	( indice pour parcourir la partie triée du tableau du haut vers le bas )
						tant que j >=0 et que temp < T[j]:
							T[j+1] = T[j] ( on décale les éléments vers la droite )
						fin tant que
						T[j+1] = temp ( on place l'élément à sa place )
					fin pour
					renvoyer T

Complexité

Raisonnement tout à fait similaire au précédent ( 2 boucles imbriquées ): la complexité du tri par insertion est aussi quadratique.

Cependant, il s'agit de la complexité dans le pire des cas ( à savoir un tableau pas du tout trié ). Or, si le tableau est déjà presque trié, l'élément à placer est très proche de sa bonne place : la boucle "tant que" ne tournera donc "pas beaucoup" à chaque placement, voire ne fera même qu'une seule itération.

Conséquence : dans cette situation, la complexité de la boucle "tant que" se rapproche de O(1), et la complexité globale devient alors O(n) soit linéaire !

L'efficacité du tri insertion est donc meilleure si le tableau initial possède un certain ordre. Cette propriété fait qu'on l'utilise pour "finir le travail" de méthodes plus efficaces en temps "normal" comme le tri rapide.

Version itérative


def tri_insertion(T: list)->list :
	for i in range(0,len(T)):
        temp = T[i]
        
        j = i-1
        while j >= 0 and temp < T[j]:
            T[j+1] =  T[j]
            j = j - 1
        
        T[j+1] = temp
   
   return T

Version récursive

C'est la même idée que pour le tri sélection : on remplace la boucle i par des appels récursifs sur le reste du tableau :


def tri_insertion_recurs(T, n = 0):
    if n == len(T):
        return T
    else:
        temp = T[n]
        
        j = n-1
        while j >= 0 and temp < T[j]:
            T[j+1] =  T[j]
            j = j - 1
        
        T[j+1] = temp
        return tri_insertion_recurs(T, n+1)

Tri à bulles

Encore une fois : pas au programme, mais amusant ( mais pas efficace du tout, donc pas utilisé en pratique )...

Algorithme


				fonction tri_bulles :
					entrée : un tableau T non trié
					sortie : le tableau T, trié ( c'est donc aussi un algorithme de tri en place...)
					
					pour i variant de N à 0:
						pour j variant de 0 à i-2 :
							si T[j] > T[j+1]:
								échanger T[i] et T[i+1]
							fin si
						fin pour
					fin pour

Version itérative


def bulles(T: list)->list :
    for i in range(len(T),-1,-1):
        for j in range(i-1):
            if T[j] > T[j+1]:
                T[j], T[j+1] = T[j+1], T[j]	
                
    return T

Version récursive


def tri_bulles_recurs(T: list, fin: int)->list:
    if fin == -1:
        return T
    else :
        for i in range(fin-1):
            if T[i] > T[i+1]:
                T[i], T[i+1] = T[i+1], T[i]
        return bulles_recurs(T, fin-1)