
Les listes dont on parle dans ce chapitre seront la plupart du temps implémentées sous forme de tableaux, car les algorithmes utilisés s'y prêtent mieux. Certains ne sont même utilisables qu'avec des tableaux, et pas avec des listes chaînées.
On cherche à déterminer si une valeur donnée N se trouve ou pas dans une liste L.
Voila un travail que vous avez déjà fait l'année dernière, cette première partie devrait donc aller assez vite...
Par algorithme "naïf", on entend "évident, trivial, sans aucune considération d'optimisation ou de rapidité".
C'est donc la façon de faire qui "vient immédiatement à l'esprit" : on parcourt toute la liste jusqu'à y trouver la valeur recherchée...
recherche_seq qui :
True si la valeur n se trouve dans la liste ou False sinonVous vous souvenez de cet algorithme ? C'est celui qu'il faut utiliser pour gagner au jeu du "nombre à deviner" en un minimum d’essais. En voila les grandes lignes :
L'idée est de couper la liste en 2, on se retrouve avec 2 sous-listes de taille identique ( à un élément près dans le cas où le nombre total d'éléments de la liste est impair, mais ce n'est pas un problème ).
On garde uniquement la sous-liste qui peut contenir la valeur recherchée : comme les sous-listes sont aussi triés, ce n'est pas difficile à déterminer,
il suffit de comparer la valeur avec l'élément délimitant les deux sous-listes, c'est à dire l'élément au milieu de la liste.
On recommence le processus tant que les sous-listes ne sont pas vides : si l'on arrive à une liste ne contenant plus aucun élément, c'est que le valeur recherchée n'était pas présente.
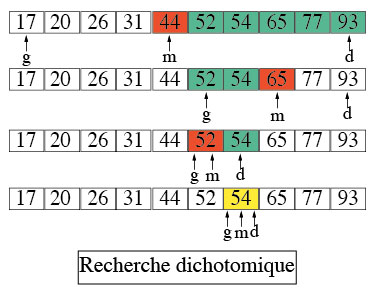
Valeur à rechercher :
Nombre d'étapes :
Voici l'algorithme itératif de la recherche dichotomique; on part du principe que la liste est implémentée sous forme d'un tableau :
tant que la "zone de recherche" ( initialement, c'est le tableau entier ) n'est pas vide :
si la valeur est égale à l'élément au milieu de la "zone de recherche" :
alors on a trouvé la valeur, on renvoie VRAI et l'indice de la valeur
sinon :
si la valeur est PLUS PETITE que l'élément au milieu :
alors elle se trouve forcément dans la partie GAUCHE de la "zone de recherche" : on recommence la recherche dans cette partie GAUCHE
sinon si la valeur est PLUS GRANDE que l'élément au milieu :
alors elle se trouve forcément dans la partie DROITE : on recommence la recherche dans cette partie DROITE
La "zone de recherche" ne contient plus aucun élément : on n'a pas trouvé la valeur : on renvoie donc FAUX
rech_dicho_iter réalisant la recherche dichotomique d'une valeur n dans une liste L triée.Cette année, vous avez les outils pour écrire la version récursive de la recherche dichotomique, d'autant plus que l'algorithme se formule beaucoup plus naturellement en récursif qu'en itératif !
Écrire une fonction récursive rech_dichoR(L, n) de la recherche dichotomique.
La taille de la liste L est initialement de n éléments; le principe de l'algorithme est de diviser par 2 la liste : à chaque "tour", on ne garde donc que la moitié des éléments, jusqu'à arriver à une liste n'ayant qu'un seul élément.
A chaque étape, on ne fait qu'une comparaison, donc une opération de complexité en O(1); la complexité de l'algorithme est donc : "O(nombre de divisions par 2)"
Il faut donc se poser la question : quel est le nombre k divisions par 2, que l'on doit faire pour, partant de n éléments , arriver à un seul ?
Donc, quelle est la valeur de k qui vérifie : n / 2k = 1 → 2k = n ?
Mathématiquement, la solution d'une telle équation est la fonction appelée logarithme en base 2 de n ( log2 n ) : k = log2 n
Vous pouvez simplement retenir ceci : le logarithme de base 2 de n est l'exposant de la puissance de 2 qui est égale à n.
Conclusion : la complexité en temps de la recherche dichotomique est donc O(log2n) ( que l'on note simplement O(log n) ) ce qui est la meilleure complexité après O(1), et bien meilleure que O(n) :
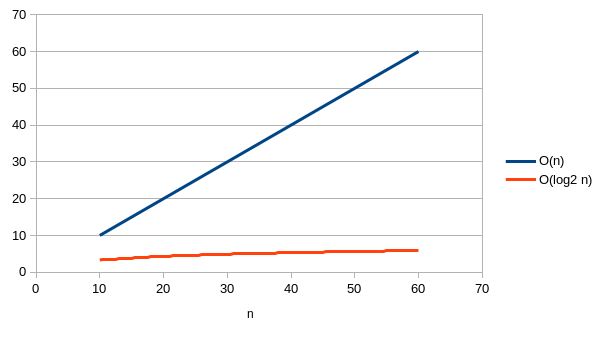
Une autre façon de voir (ou prédire) la complexité logarithmique est de remarquer que même si l’on double la taille de l’entrée (i.e., une séquence de taille 2n au lieu de n), on n’a besoin que d’une étape de plus pour effectuer la recherche...
En général, on retrouve une complexité logarithmique dans tous les algorithmes qui contiennent une boucle divisant une quantité de donnée par une constante à chaque itération.
L'algorithme de recherche dichotomique est donc bien plus efficace en temps que la recherche séquentielle ( ce ne serait pas vrai pour une liste non triée )
Quelle est la raison à ce fait ? Dans le premier algorithme, à chaque tour de boucle, le nombre de données restant à traiter ne diminuait que de 1 unité à la fois; dans le deuxième, à chaque "tour" ( en fait ici, à chaque appel récursif ), on divise par 2 le nombre de données à traiter.
C'est le principe appelé diviser pour régner qui est utilisé ici : l'algorithme de recherche dichotomique travaille donc à chaque fois sur un problème dont la taille a été divisée ( ici par 2 ), la solution globale étant finalement obtenue à l'issue de la résolution de chacun de ces "sous-problèmes".
Cependant, la recherche dichotomique nécessite auparavant que la liste ait été triée, ce qui a un coût, alors que la recherche séquentielle n'a pas cette précondition.
Cependant, une fois la liste triée, plusieurs recherches se feront alors avec une complexité toujours plus faible ( O(log n) ) qu'avec la recherche séquentielle ( O(n) ).
Autre inconvénient de la recherche dichotomique : elle n'est pas utilisable avec une structure de liste chaînée.
Le principe du diviser pour régner s’applique à tout problème qui peut être séparé en plusieurs sous-problèmes de taille plus petite ( dans l'exemple de la recherche dichotomique, c'est la recherche dans une liste de taille moitié de la précédente ), que l'on "découpe" du plus grand au plus petit jusqu’à obtenir un problème élémentaire que l'on sait résoudre de manière évidente.
Si tous les sous-problèmes peuvent être résolus de manière similaire ( par exemple, couper une liste en deux parties ), c'est du coup un principe qui se prête très bien à la récursivité ( le "problème élémentaire" = le cas de base ! ) :
Il faut bien insister sur le fait que ces sous-problèmes doivent être semblables au problème global : dans le cas de la recherche dichotomique par exemple, il s'agit dans tous les cas d'une recherche dans une liste.
Dans l'exemple de la recherche dichotomique, les deux premiers aspects apparaissent bien :
L'aspect "Combiner" n'apparaît pas puisque la solution du problème est directement donnée par celle du plus petit des sous-problèmes ( liste à un seul élément )...cet aspect apparaît beaucoup mieux dans un autre exemple classique, celui du tri fusion.
Les méthodes de tri "naïves" comme le tri par sélection, le tri par insertion ( vues en Première ) ou le tri à bulles sont toutes de complexité en O(n2), ce qui n'est pas très bon...on a donc recherché d'autres méthodes plus efficaces pour trier les très grandes listes.
L'algorithme de tri-fusion a été élaboré par John Von Neumann en 1945.
Le principe général du tri par fusion est le suivant :
Soit l'algorithme :
fonction tri_fusion ( TABLEAU T[0:n])
si T ne contient qu'un seul élément
renvoyer T
sinon
gauche = partie_gauche de T
droite = partie_droite de T
gauche = tri_fusion (gauche)
droite = tri_fusion (droite)
renvoyer fusion(gauche, droite)
La fonction fusion() est le centre de l'algorithme : les listes gauche et droite sont forcément triées, leur
fusion est donc peu coûteuse en temps ( cf. ci-dessous). C'est grâce à cela que l’algorithme de tri fusion est efficace : sa complexité est
O(n.log n) ( quasi-linéaire, intermédiaire entre O(n) et O(n2) ).
Dérouler l'exécution de cet algorithme pour la liste [3, 5, 4, 1, 0, 6, 2].
La fonction de fusion va créer une nouvelle liste, élément par élément, en "piochant" dans les deux-listes à fusionner les éléments à ajouter pour construire la liste fusionnée.
Pour cela, on compare chacun des premiers éléments des deux listes à fusionner :
On s'arrête quand une des listes "gauche" ou "droite" est vide.
Ce principe de comparaison des premiers éléments est optimal car, dans l'algorithme de tri-fusion, les deux listes à fusionner sont déjà triées.

fusion qui :
fusion de manière récursive.Écrire une fonction tri_fusion qui :
fusion ( ou fusion_rec ) précédente.