NSI Terminale
NSI Terminale
Les graphes sont des structures de données qui permettent de représenter les relations qui existent entre différentes informations.
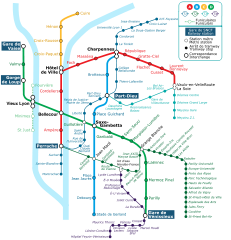
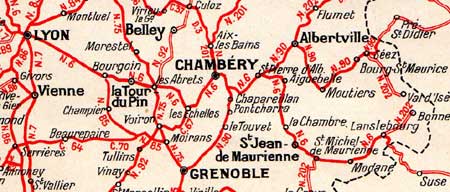
Un plan de métro ou une carte routière peut être vu comme un graphe modélisant les routes qui relient une station ou une ville à une autre.
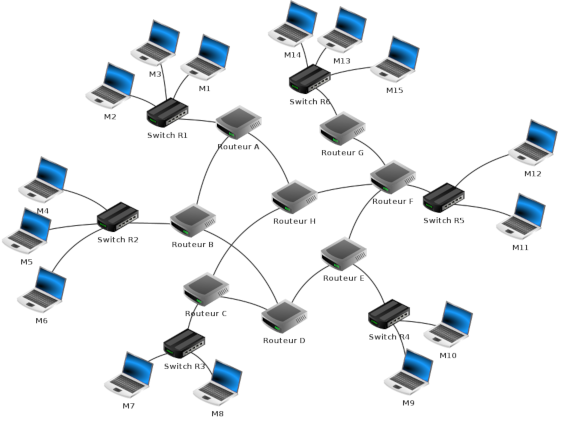
Tout réseau informatique peut par exemple être représenté par un graphe, indiquant les liaisons qui existent entre les différentes machines, routeurs, etc... du réseau.
On peut également représenter par un graphe les relations qui existent entre des personnes dans un groupe donné ( entreprises par exemple ) ou sur un réseau social.
Mais les graphes se retrouvent dans d'autres situations où on s'attend moins à les trouver, comme par exemple la recherche du chemin dans un labyrinthe, la résolution de certains jeux ou la coloration des cartes géographiques !
Un graphe est constitué :
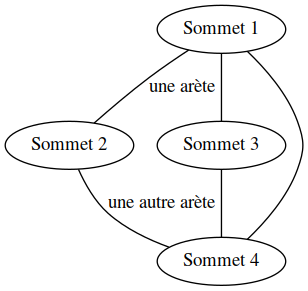
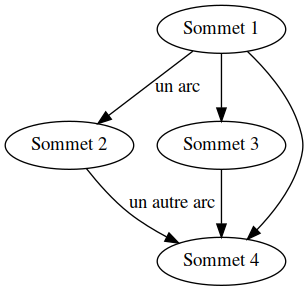
Dans un graphe non orienté, deux sommets sont voisins ( ou adjacents ) si ils sont reliés par une arête.
Sommet 1 et Sommet 4 sont voisins, Sommet 2 et Sommet 3 ne le sont pas.
On appelle degré le nombre de voisins d'un sommet.
Le degré de Sommet 1 est 3, celui de Sommet 3 est 2.
Dans le cas d'un graphe orienté, on parlera plutôt de successeurs ou prédécesseurs d'un sommet selon le sens de l'arc joignant les sommets.
Ainsi, Sommet 4 est un successeur de Sommet 1, Sommet 2 est un prédécesseur de Sommet 4.
Un sommet peut très bien être relié à lui-même par une boucle.
Un graphe peut être valué ou pondéré. On associe dans ce cas à chaque arc ou arête une valeur numérique. Cela permet d'indiquer que certaines relations ont plus de "poids" que les autres dans le graphe, comme par exemple dans un réseau informatique une liaison entre deux routeurs plus rapide que les autres.
La ville de Königsberg était une ville de Prusse puis une des principales villes de l'Empire Allemand avant d'être cédée à l'URSS en 1945. Cette ville est désormais appelée Kaliningrad et fait partie de la Fédération de Russie.
Cette ville s'étendait au XVIIIe siècle autour de deux îles situées sur le fleuve Pregel. Ces deux îles étaient reliées entre elles par un pont. Six autres ponts reliaient les rives de la rivière à l'une ou l'autre des deux îles, comme représenté sur le plan ci-contre.
La légende raconte que certains habitants de cette ville cherchaient lors de promenade à passer une fois et une seule par chacun des ponts pour revenir au point de départ.
Est-ce possible ? Si oui, par quel chemin ?
Les habitants ont cherché des solutions et l'un d'eux, le grand mathématicien Euler, a réussi en 1735 à répondre à la question précédente.
Pour cela, il a développé des outils mathématiques à la base de la théorie des graphes.
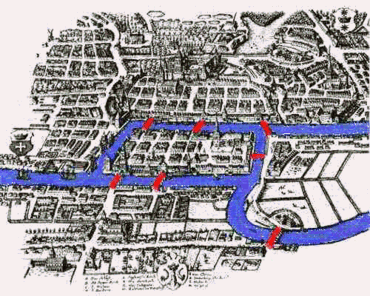
Représenter la situation à l’aide d’un graphe en précisant ce que représentent ici arêtes et sommets.
Pouvez-vous trouver la réponse à la question posée à Euler par les habitants de Königsberg ?
Donner le graphe de ce réseau d’ami :
| Utilisateur | Ami avec |
| Anne | Léa, Cyril, Paul, Yvan |
| Paul | Anne, Yvan, Léa |
| Cyril | Léa, Anne, Yvan |
| Yvan | Emy, Marc |
| Jean | Emy, Marc |
| Marc | Jean, Emy |
| Emy | Jean, Marc |
Voici ci-contre le plan d’un musée : les parties grisées matérialisent les portes et les visiteurs partent de l’accueil, visitent le musée et doivent terminer leur visite à la boutique.
Représenter la situation à l’aide d’un graphe en précisant ce que représentent ici arêtes et sommets.
On souhaite organiser un tournoi de football avec 4 équipes ( numérotées de 1 à 4).
Chaque équipe rencontre une seule fois toutes les autres.
Un club de tennis doit sélectionner deux joueurs parmi quatre pour représenter le club à un tournoi national.
Les quatre joueurs sont notés A, B, C et D. Pour réaliser la sélection, le club organise des matchs : chaque joueur rencontre les trois autres.
Règle :
Les joueurs sélectionnés sont les joueurs ayant obtenu le plus grand nombre de points.
On donne le résultat sous la forme d’un graphe orienté ABCD. Le sens de l’arc A → B indique que le joueur A a battu le joueur B.
Dans ce film de 1995, Bruce Willis et Samuel Jackson sont confrontés à un méchant qui les oblige à résoudre des énigmes afin de sauver la vie de milliers de personnes...
Un des problèmes est le suivant : les deux personnages ont, en leur possession, deux bidons non gradués, un pouvant contenir cinq litres, et l'autre trois litres.
Il y a une fontaine à proximité. Comment faire pour avoir quatre litres dans le bidon de cinq litres, sans bien sûr avoir recours à un instrument de mesure ?
Le problème peut être modélisé par un graphe, dont les sommets sont les états des deux seaux ( c'est à dire le volume d'eau qu'ils contiennent à un moment donné ), et les relations, la possibilité de passer d'un état à l'autre.
L'énigme consiste donc à trouver un chemin entre les sommets (0,0) et (4,0) en effectuant des passages "permis" par la contenance des deux seaux. On peut ainsi passer de l'état (5,0) à l'état
(3,2) en remplissant le seau de 3 L avec une partie de celui de 5L; par contre, on ne peut pas passer de l'état (2,3) à celui de (4,2) ( par exemple ) car on ne sait pas transvaser
un volume de 1 L d'un seau à l'autre...
Le graphe comporte 24 sommets correspondant aux 24 états possibles selon le remplissage de chacun des seaux; ces sommets sont représentés ci-dessous :
A vous de trouver l'ensemble des relations à suivre dans ce graphe ( en respectant bien entendu les contraintes ! ) pour résoudre l'énigme.
Il faut maintenant réfléchir à la manière de représenter un graphe en mémoire d'un ordinateur.
De quoi a-t-on besoin de pour décrire des graphes ?
De toute évidence, il nous faut pouvoir représenter :
Lors de notre représentation des arbres binaires, nous avions choisi de ne considérer que les nœuds et nous avions essentiellement une structure sous forme de triplet :
arbre = (étiquette, fils_gauche, fils_droit).
Cela ne fonctionne plus ici, il n’y a généralement pas de sommet privilégié dans un graphe, tous les nœuds jouent le même rôle.
Il faut donc envisager un moyen de représenter l’ensemble des relations entre sommets.
La méthode la plus simple et la plus courante pour décrire les arêtes/les arcs est d’en donner une liste pour chacun des sommets.
A chacun des sommets, on associera alors sa liste d'adjacence, c'est à dire l'ensemble de ses voisins ( ou de ses successeurs ) pour représenter les arêtes ( ou les arcs ).
Dans le cas de Python, l'ensemble des listes d'adjacence seront implémentées sous la forme dictionnaire dont :
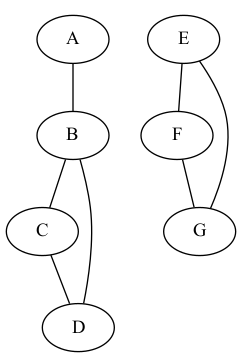
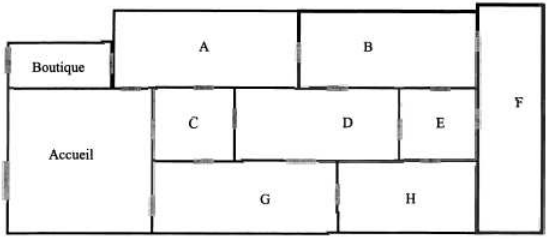
Pour le graphe non orienté ci-contre, on aurait ainsi :
| Ensemble des sommets | Ensemble des arêtes |
| A | B, C, D |
| B | A, D |
| C | A, D |
| D | B, C, A |
En Python, le graphe correspondra donc au dictionnaire :
graphe = {
'A': ['B', 'C', 'D'],
'B': ['A', 'D'],
'C': ['A', 'D'],
'D': ['B', 'C', 'A']
}
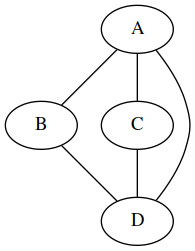
Pour le graphe orienté ci-contre, on n'indiquera que les successeurs de chaque sommet :
| Ensemble des sommets | Ensemble des arcs |
| A | B, C, D |
| B | D |
| C | D |
| D | B |
En Python :
graphe = {
'A': ['B', 'C', 'D'],
'B': ['D'],
'C': ['D'],
'D': ['B']
}
Remarque : une alternative serait aussi bien de représenter la liste des prédécesseurs de chaque sommet.
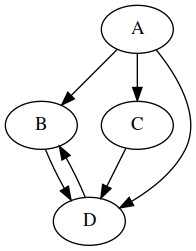
Et pour un graphe pondéré ?
Dans ce cas, il faut indiquer une information en plus dans la liste des arêtes/des arcs, à savoir le poids de chaque relation, par exemple sous forme d'un tuple en Python :
graphe = {
'A': [('B', 5), ('C', 2), ('D', 6)],
'B': [('A', 5), ('D', 3)],
'C': [('A', 2), ('D', 9)],
'D': [('B', 3), ('C', 9), ('A', 6)]
}
Pour un graphe ni orienté, ni pondéré :
Une matrice d'adjacence est un tableau de taille n ⨯ n ( n = nombre de sommets ); chaque ligne et chaque colonne correspond à un des sommets du graphe.
Chaque case à l'intersection d'une ligne et d'une colonne de la matrice contient :
En Python, une matrice sera implémentée par un tableau de tableaux.
L'avantage de cette représentation est que l'on "voit" immédiatement quels sont les voisins de tel ou tel sommet.
L'inconvénient est que la matrice d'adjacence est souvent "vide", c'est à dire qu'elle occupe une grande place en mémoire pour finalement peu d'information...
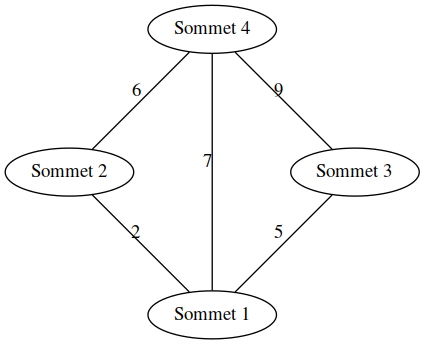
Dans le cas du graphe non orienté ci-contre, la matrice d'adjacence serait :
| A | B | C | D | |
| A | 0 | 1 | 1 | 1 |
| B | 1 | 0 | 0 | 1 |
| C | 1 | 0 | 0 | 1 |
| D | 1 | 1 | 1 | 0 |
Le tableau de tableaux Python correspondante serait alors :
graphe = [[0, 1, 1, 1],
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 1, 1, 0]]
On remarque qu'un sommet n'est pas "relié à lui-même" ( attention, sauf si il existe une boucle ! ).
Pour un graphe orienté, on prendra par exemple la convention suivante :
Les arcs sont donc orientés des lignes vers les colonnes.
Dans le cas du graphe orienté ci-contre, la matrice d'adjacence serait :
| ↱ | A | B | C | D |
| A | 0 | 1 | 1 | 1 |
| B | 0 | 0 | 0 | 1 |
| C | 0 | 0 | 0 | 1 |
| D | 0 | 1 | 0 | 0 |
En Python :
graphe = [[0, 1, 1, 1],
[0, 0, 0, 1],
[0, 0, 0, 1],
[0, 1, 0, 0]]
Pour un graphe pondéré, on remplacera les booléens par le poids respectif de chaque arête/arc :
graphe = [[0, 5, 2, 6],
[5, 0, 0, 3],
[2, 0, 0, 9],
[6, 3, 9, 0]]
Ces façons de représenter un graphe sont basées sur des conventions, que l'on peut bien entendu faire évoluer, à condition que l'interface de la structure de données soit bien claire !
Ce paragraphe est tiré de la page http://www.monlyceenumerique.fr/nsi_terminale/sd/sd5_graphe.php ( © CC-BY-NC-SA )
Cela dépend de :
la structure du graphe : plus un graphe est "dense", c'est-à-dire plus il y a d'arêtes (ou d'arcs) pour un nombre donnés de sommets, plus la matrice d'adjacence est pertinente.
En effet, considérons un graphe avec n sommets et m arêtes :
la complexité en mémoire d'une matrice d’adjacence est en O(n2).
la complexité en mémoire d'une tableau de tableaux d’adjacence est en O(n+m).
le travail à faire sur ce graphe : vous verrez dans un prochain chapitre des algorithmes pour étudier et travailler avec des graphes. Certains algorithmes nécessiteront d'implémenter le graphe d'une manière plutôt qu'une autre.
Dès maintenant, vous pouvez comprendre que pour un graphe à n sommets :
si on veut tester que deux sommets sont adjacents ou non :
on a une complexité en temps en O(1) pour une matrice d'adjacence (lecture directe d'un terme de la matrice)
mais en O(d) pour une liste d'adjacence où d correspond au nombre de voisins du sommet testé ( on doit, dans le cas où il n'y a pas d'arête reliant les sommets, balayer toute la liste des sommets voisins )
L'implémentation sous forme de matrice d'adjacence est préférable alors.
si on veut itérer sur les voisins d'un sommet :
on a une complexité en temps en O(n) pour une matrice d'adjacence (lecture de tous les termes d'un même ligne (ou colonne) pour connaître quels sont les sommets voisins)
mais en O(d) pour une liste d'adjacence ( on doit balayer toute la liste des sommets voisins )
L'implémentation sous forme de liste d'adjacence est préférable alors.
Les figures ci-dessous tracent des graphes aléatoires; vous pouvez zoomer le graphe, le déplacer, déplacer les nœuds pour mieux le voir.
Pour quelques uns de ces graphes, représentez le dictionnaire des listes d'adjacence ainsi que la matrice d'adjacence du graphe.
Ne vous limitez pas à des graphes trop "simples"...
| Listes d'adjacence | Matrice d'adjacence |
|---|---|
|
|
L'exercice inverse : représenter le graphe dont, soit le dictionnaire des listes d'adjacence, soit la matrice d'adjacence est donné(e).
Enfin, passer d'une représentation à l'autre :
