TP Algorithme PageRank

Principe

Le PageRank est un algorithme utilisé par Google pour mesurer la popularité d'un site ou d'une page web.

C'est un algorithme inventé par Larry Page, un des fondateurs de Google, en 1997.

Cet algorithme se sert ( notamment ) des liens entrants vers un site pour évaluer la popularité de ce site : plus il y a de liens "pointant" vers une page web, plus celle-ci sera "populaire", et donc meilleur sera son score PageRank.

Mais l'algorithme tient également compte de la "qualité" de ces liens : les liens entrants provenant d'une page ayant elle-même un PageRank élevé pèseront plus dans le PageRank d'un site donné.

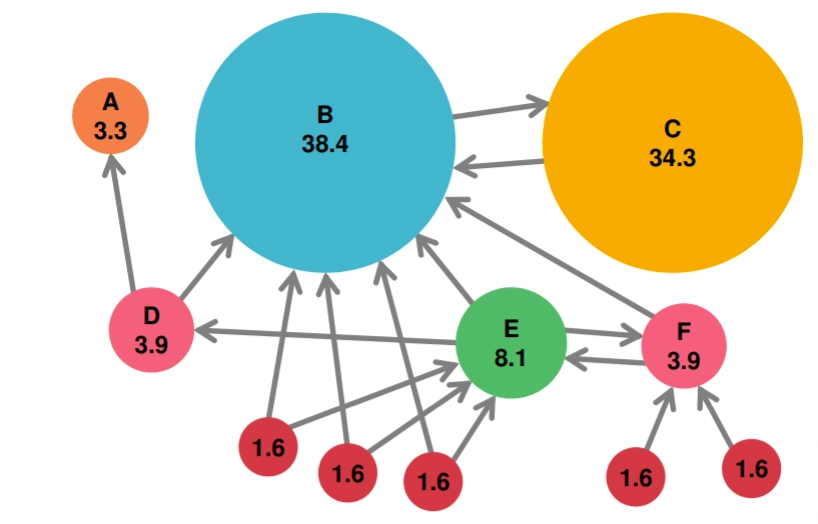
Les pages web et les liens entre elles peuvent être modélisé(e)s par un graphe, dans lequel les pages sont les sommets, et les liens entre pages, des arcs entre les sommets ( c'est donc un graphe orienté ) :

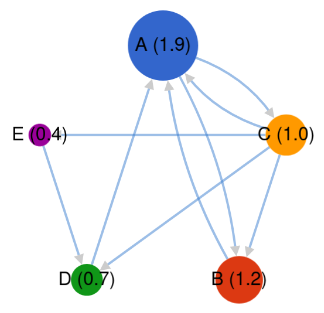
Intuitivement, un sommet dans un graphe aura un PageRank élevé si la somme des PageRank des sommets d'où proviennent ses liens entrants est élevée. Ainsi, le PageRank d'un sommet dépend non seulement du nombre de liens entrants qu'il possède, mais aussi de l'importance des sommets d'où ces liens proviennent . Par exemple, si un sommet n'a qu'un seul lien entrant d'un autre sommet , mais que ce dernier a un PageRank élevé, alors le sommet aura également un PageRank relativement élevé.

Un exemple concret est le graphe représentatif d'un réseau social, les arcs indiquant qui suit qui : un arc dirigé de l'utilisateur A vers l'utilisateur B existe si A suit B.
Des personnes célèbres comme Barack Obama ont des millions d'abonnés, dont certains sont également célèbres avec des millions d'abonnés. Ainsi, ces utilisateurs, lorsqu'ils sont représentés sous forme de sommets dans un graphe, auront un PageRank élevé. De plus, le PageRank élevé de ces célébrités contribuera au PageRank des utilisateurs qu'ils suivent. Si Barack Obama suit un autre utilisateur et est le seul follower de cet utilisateur, cet utilisateur aura toujours un PageRank relativement élevé.

Nous allons utiliser deux approches pour simuler un fonctionnement simplifié de l'algorithme PageRank :

la marche aléatoire dans un graphe
le calcul direct du score PageRank des pages

Nous travaillerons sur le graphe ci-dessus, dont voici le dictionnaire Python des listes d'adjacence :


{
'A': ['B','C'],
'B': ['A'],
'C': ['A', 'B', 'D', 'E'],
'D': ['A'],
'E': ['D']
}

Première approche : marche aléatoire dans un graphe

L'algorithme peut être vu comme le déplacement aléatoire d'un utilisateur, qui se déplace de page en page en cliquant au hasard sur les liens hypertexte qu'il y a entre elles : plus son parcours le fait revenir sur une page donnée, plus cette page est "populaire", et donc plus le PageRank de cette page sera élevé...

Plus formellement, il s'agit donc du parcours aléatoire des sommets d'un graphe, en "empruntant" au hasard un des arcs passant d'un sommet à un autre; en comptant le nombre de fois où ce parcours aléatoire fait repasser par le même sommet, on peut alors évaluer la "popularité" de ce dernier : plus ce nombre est élevé, plus le sommet est "populaire".

Bien entendu, dans un "grand" graphe, il faut un nombre d'itérations n important de l'algorithme pour avoir des résultats significatifs !...
Pour une grande valeur de n, le rapport n(sommet)n tend alors vers la probabilité ( entre 0 et 1 ) que le sommet soit rencontré dans le parcours.

( C'est beaucoup mieux expliqué ici; d'ailleurs, le PageRank de ce site est de 5, alors que celui de nsivaugelas n'est que de 2 😶 ...)

Écrire une fonction pagerank_random, qui :

prend comme paramètres le graphe g modélisant le réseau de pages web étudié, et un nombre n d'itérations
renvoie un dictionnaire, dont les clés sont les sommets du graphe, et les valeurs, la probabilité que le sommet soit rencontré dans le parcours ( initialisée à 0 au début de l'algorithme ).

Le "PageRank" sera calculé en parcourant aléatoirement pendant n itérations les sommets du graphe. Le sommet de départ sera lui-même choisi aléatoirement.

Pour sélectionner aléatoirement un élément dans un tableau Python, utiliser la fonction choice du module random


choice(['A', 'B', 'C', 'D'])
>>> 'C'

Créer le graphe correspondant au réseau en exemple; faire 5 itérations de l'algorithme sur ce graphe, puis 10, 50, 100, ... Que constate-t-on ?

from random import choice def pagerank_random(g, n: int)->dict: pass pr = { 'A': ['B','C'], 'B': ['A'], 'C': ['A', 'B', 'D', 'E'], 'D': ['A'], 'E': ['D'] }

SOLUTION

Deuxième approche : calcul direct du PageRank

Principe

Le calcul du PageRank modélise un internaute théorique. Étant donné que l'internaute se trouve sur une page Web particulière, l'algorithme suppose qu'il suivra l'un des liens sortants avec une probabilité égale.

Pour un sommet v, qui a N(v⁺) liens sortant, alors la probabilité que l'internaute suive au hasard un de ces liens est :

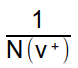
Si il existe un arc entre le sommet v et un sommet u, alors la contribution de v au PageRank de u sera le produit du PageRank de v par la probabilité que l'internaute suive le lien de v vers u :

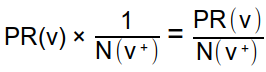
Le PageRank total de u sera alors la somme des contributions de tous les sommets v qui ont un lien sortant vers u :

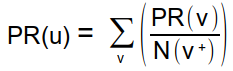
Cependant, cette relation ne tient pas compte du fait que certaines pages sont des drains, c'est à dire des pages vers lesquelles aboutissent des liens, mais desquelles aucun n'en sort : impossible pour "l'internaute aléatoire" de "sortir" de ces pages !
On suppose alors que l'internaute, après avoir suivi au hasard quelques hyperliens, recommencera à zéro. On lui accorde donc, à l’arrivée sur une page, une petite probabilité de quitter la page courante pour reprendre une page au hasard.
On introduit ainsi un facteur d'amortissement, d, dont la valeur est généralement fixée à 0,85, qui permet de tenir compte de cette probabilité :

u est la page dont on cherche à calculer le PageRank
v sont les pages ayant un lien sortant vers u ( c'est à dire qu'il existe un arc de v vers u )
N(v⁺) est le nombre total de liens sortant d'un sommet v
d est le facteur d'amortissement ( d'après cette formule, chaque page a donc toujours une probabilité de 1 - d d'être choisie au hasard ).

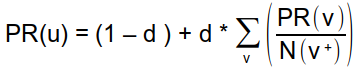
On voit que cette formule est circulaire : pour calculer le PageRank d'une page, il faut déjà connaître celui des autres pages, qui lui-même....
Ce n'est pas paradoxal, l'algorithme procède ainsi :

au début, le PageRank de chaque page est initialisé à la même valeur de probabilité, à savoir 1.
on procède ensuite au calcul du PageRank de chaque page, en appliquant la formule de calcul ci-dessus;
on recommence alors plusieurs fois de suite cette opération : au bout d'un certain temps, on constate que l’algorithme converge, c'est à dire que les valeurs de PageRank se stabilisent.
Pour savoir quand cette convergence est atteinte, on peut soit faire "tourner" l'algorithme un nombre de fois prédéterminé ( ce sera notre approche ), ou alors déterminer quand la variation de la valeur du PageRank de chaque page entre deux itérations devient inférieure à un certain seuil.


PR ← tableau des valeurs de PageRank de chaque sommet initialisés à 1

pour n iterations de l'algorithme:
    pour chaque sommet u du graphe:
        s ← 0
        pour chaque sommet v du graphe ayant un arc vers u:    
            s ← s + PR[v]/nombre total de liens sortants de v
        PR[u] ← (1-d) + d * s
renvoyer PR

Sur ce simulateur de calcul, on peut voir le détail des calculs du PageRank des sommets d'un graphe pour un nombre donné d'itérations de l'algorithme ( 4 par défaut ).

Implémentation

Dans cet algorithme, on a besoin de savoir si un arc existe entre deux sommets : l'implémentation du graphe sous forme de matrice d'adjacence est donc bien adaptée.

construire la matrice d'adjacence associée au graphe en exemple; vous pouvez éventuellement utiliser la fonction qui vous aviez écrite pour transformer une liste d'adjacence en matrice.
compléter le code ci-dessous qui implémente l'algorithme de calcul PageRank.
utiliser l'algorithme avec 5, puis 10, 20, ... itérations.
que constate-t-on quand le coefficient d’amortissement devient petit ? Comment l'interpréter ?
ajouter au graphe un (ou plusieurs) drain(s), et relancer l'algorithme; que constate-t-on ?

from graphe import * # Facteur d'amortissement : d = 0.85 def nbre_liens_sortants(m: list[list], v: int)->int: """ Fonction qui renvoie le nombre total de liens sortants d'un sommet donné. Entrée : m = la matrice d'adjacence du graphe v = l'indice du sommet dans la matrice Sortie : le nombre total de liens sortants de v """ pass def pagerank_calcul(m: list[list], n: int)-> list: """ Fonction qui applique l'algorithme de calcul du PageRank des sommets d'un graphe. Entrées : m = la matrice d'adjacence n = nombre d'itérations de l'algorithme Sortie : le tableau des PageRank de chaque sommet """ pass pr = { 'A': ['B','C'], 'B': ['A'], 'C': ['A', 'B', 'D', 'E'], 'D': ['A'], 'E': ['D'] }

SOLUTION

Pour terminer...

Vous pouvez utiliser la fonction ci-dessous pour générer une matrice d'adjacence aléatoire, visualiser le graphe correspondant ( avec le module Graphviz ), et utiliser ensuite l'algorithme PageRank pour déterminer la "page" la plus populaire ( et vérifier visuellement ) :

from graphviz import Digraph from random import randint def genere_graphe(N: int, p: int)->list[list]: """ Génère la matrice d'adjacence d'un graphe orienté aléatoire. Affiche également le graphe. Entrée : N = le nombre de sommets p = probabilité de créer un arc entre deux sommets ( 1 <= p <= 100 ) Sortie : la matrice d'adjacence du graphe """ assert 1 <= p <= 100, "La probabilité p doit être comprise entre 1 et 100." m = [[1 if i != j and randint(1,100) < p else 0 for j in range(N)] for i in range(N)] g = Digraph() for i in range(len(m)): for j in range(len(m)): if m[i][j] == 1: g.edge(str(i), str(j)) g.view() return m

Conclusion

Le véritable algorithme PageRank, encore utilisé par Google, tient compte de nombreux autres facteurs pour mesure la popularité d'une page : contenu, ancres dans la page, le trafic sur la page, etc...

C'est d'ailleurs devenu une "boîte noire" dont on ne connaît pas vraiment les facteurs utilisés et leur poids dans la mesure finale...

PageRank peut avoir d'autres applications que la mesure de popularité d'une page: il peut être utilisé pour déterminer la centralité dans un graphe, c'est à dire déterminer les sommets les plus importants, pour des applications comme la mesure d'audience, ou les algorithmes de recommandation.