
Une liste est une façon d'organiser des données, ce que l'on appelle une structure de données, destinée à pouvoir accéder librement à chacune de ces données.
Une liste est aussi appelée une collection, ou une séquence d'éléments, chaque élément contenant une donnée.
Les éléments sont repérés selon leur rang ( = indice ) dans la liste.
L’ordre des éléments dans une liste est fondamental : ce n’est pas un ordre sur les valeurs des éléments, mais un ordre sur les places des éléments.

Hormis les données elle-mêmes, il faut disposer de certaines opérations qui permettent de manipuler la structure de données :
Tout dépend de ce dont l'utilisateur a besoin pour faire fonctionner son code !
Les listes peuvent être représentées en mémoire de différentes façons; vous en verrez deux :
par un tableau : chaque élément de la liste peut être désigné par sa place dans la séquence, à l’aide de son indice.
Pour accéder à un élément déterminé, on utilise le nom de la variable qui contient la liste et on lui accole entre deux
crochets, l’index numérique qui correspond à sa position.
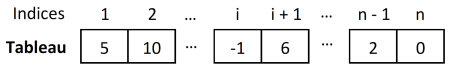
par une liste chaînée : Chaque maillon est un objet dans lequel on stocke l’élément et une information pour trouver
le suivant (voire aussi le précédent dans des versions plus évoluées).
On n'a un accès direct qu'au premier maillon d'une liste chaînée, mais il faut parcourir tous les maillons précédents pour accéder à
un élément donné.

On constate donc que :
Dans cette implémentation, une liste est représentée en mémoire par un tableau, c'est à dire une succession de cases mémoires contiguës ( = les unes à la suite des autres ), la nième case du tableau correspondant au nième élément de la liste.
Ce tableau est généralement statique, c'est à dire d'une dimension fixée à sa création : il ne peut pas être "rallongé" ou "raccourci" de manière simple.
Les éléments stockés dans une liste sous forme de tableau doivent être du même type, sauf si, au lieu de stocker directement l'élément, on stocke en réalité son adresse en mémoire ( c'est ce que fait par exemple Python ); la liste contient alors des références vers les éléments, et pas les éléments eux-mêmes.
Dans le cas de Python, attention à la confusion entre les termes : les listes Python sont en fait des tableaux dynamiques ( c'est à dire d'une dimension qui peut évoluer en fonction de la quantité de données à y stocker ), pouvant contenir des éléments de différents types, et fournissant des fonctionnalités analogues à ceux d'une liste; il ne faut donc pas les confondre avec le TAD LISTE.
L'intérêt de l'utilisation d'un tableau est que l'accès à un de ses éléments se fait en temps constant ( complexité O(1) ), ce qui signifie que le temps d'accès ne dépend pas du nombre de données stockées, donc de la taille de la liste.
Ceci vient du fait que les éléments d'un tableau sont stockés en mémoire à des adresses contiguës les unes des autres, et qu'il suffit donc de connaître l'adresse en mémoire du début du tableau pour accéder par décalage ( "offset" ) de cette adresse à n'importe lequel de ses éléments ( et notamment son dernier ! ).

| Avantages | Inconvénients |
|---|---|
|
|
Considérons par exemple un programmeur en langage de bas niveau comme le langage C, qui n'a pas ce type à sa disposition, uniquement des tableaux de taille fixe, et qui désire implémenter le TAD Liste.
Vous allez écrire quelques méthodes qui permettraient à ce programmeur de disposer de ces fonctionnalités.
Écrire une classe ( nous serions donc plutôt en C++ 😎..) Liste , dont le constructeur prend en paramètre un entier taille correspondant à la taille désirée de la liste, et
instancie une liste sous forme d'un tableau de taille éléments "vides".
Les éléments "vides" seront codés par exemple par la valeur 0.
Écrire également la "méthode magique" __str__ qui renvoie une chaîne de caractères représentant la liste.
Vous savez comment adresser les éléments d'un tableau, en utilisant la notation usuelle liste[indice]
Pour pouvoir utiliser ce comportement dans notre liste "custom", il est nécessaire de coder deux méthodes magiques des objets Python :
__getitem__ qui renvoie la valeur d'un élément d'indice donné de la liste __setitem__ qui affecte une valeur à un élément d'indice donné dans la liste
Écrire les deux méthodes spéciales __getitem__ et __setitem__ pour notre classe Liste.
Vous pouvez alors remplir votre liste avec des éléments, par exemple des entiers, et consulter la valeur des éléments de la liste.
Bien entendu, il faudra gérer, grâce à une assertion, le cas où l'indice est "en dehors" du tableau, et retourner une erreur dans ce cas !
On aura intérêt, pour vérifier les préconditions des méthodes/fonctions que l'on écrit, à utiliser des assertions.
Les préconditions sont les conditions qui doivent être vérifiées au début d'une fonction/d'une méthode pour que tout se déroule ensuite sans erreur.
L'instruction assert permet de vérifier si une précondition est vérifiée, et en cas contraire, de générer une erreur ( Assertion Error ).
assert précondition, "Message d'erreur"
Il faut bien noter que la précondition testée est bien celle qui DOIT ÊTRE VRAIE.
Avec un tableau de taille fixe, il n'y a pas le choix dans la manière de procéder :
Ce comportement est exactement le même en Python lorsqu'on rajoute un élément en fin d'un tableau avec l'opérateur + :
tab = tab + [element] # un nouveau tableau 'tab' est en fait créé...
Écrire le code d'une méthode append qui permet d'ajouter un élément en fin de liste ( sans utiliser bien entendu l'opérateur Python + 😉 ...)
Quel est la complexité en temps de cette méthode ?
Après avoir réfléchi aux opérations à réaliser, écrire le code d'une méthode pop qui permet de supprimer le dernier élément de la
liste, et qui renvoie la valeur de cet élément.
Ces opérations, de même que celle qui permettent d'insérer et de supprimer un élément à n'importe quel indice, peuvent être très coûteuses en temps dans le cas de grandes listes car on a besoin de "déplacer" ( en fait, recopier ailleurs en mémoire ) pratiquement tous les n éléments
de la liste ( exactement : n-1 éléments ) : ce sont donc des opérations de complexité O(n).
Dès que l'on a à modifier souvent le début ( ou la fin ) d'une liste ( et surtout si la liste est très grande ! ), ce n'est donc pas l'implémentation la plus adaptée.
list de PythonUn tableau dynamique est un tableau dont la taille peut varier ("allongement" ou "raccourcissement" ), et ce de manière "automatique".
Dans le cas des tableaux Python ( type Python list, attention encore une fois à la confusion ! ), on dispose en particulier des méthodes suivantes :
tableau.append(element) : ajoute un élément en fin de tableau.element = tableau.pop() ; retire le dernier élément du tableau et le renvoietableau.insert(indice, element) : insertion à n'importe quel indiceelement = tableau.pop(indice) : suppression à n'importe quel indice et renvoi de l'élémentLes explications qui suivent, bien que très intéressantes 😊, ne sont pas des notions exigibles par le programme.
La gestion d'un tableau dynamique est une affaire de compromis entre d'une part, la rapidité d'accès à un élément d'un tableau de taille fixe, et d'autre part l'avantage d'avoir une taille de tableau variable.
Python gère cela de cette façon :
Il va sans dire que, si le tableau plein contient un très grand nombre d'éléments, ces opérations de copie peuvent prendre du temps : c'est une opération en O(n).
Cependant, cela se produit très rarement comparé aux opérations de remplissage de tableau; on considère alors ( en fait, il y a toute une "cuisine" là-derrière faite de compromis entre le choix de la taille de tableau
à partir de laquelle il faudra redimensionner, et occupation de la mémoire ) que l'ajout ( append ) et le retrait ( pop ) du dernier élément d'un tableau dynamique Python se fait en moyenne en temps constant. C'est une garantie
qu'offre d'ailleurs le langage ( et d'autres également ).
Par contre, comme dit plus haut, l'instruction tableau = tableau + [element] réserve à chaque ajout d'un élément un nouvel espace mémoire et recrée donc un nouveau tableau, ce qui est donc beaucoup
moins efficace !
Pour plus d'informations à ce sujet, vous pouvez consulter cette page.
On retiendra que, en Python, les opérations append et pop, donc en fin de liste, sont optimisées, mais le fait que l'implémentation soit sous forme de tableau,
il a les mêmes limitations au niveau des insertions/suppressions en n'importe quel autre endroit de la liste...
Les éléments d'une liste chaînée sont appelés cellules ou maillons, et contiennent non pas une seule information, mais deux :
On a donc ici affaire à une chaîne de cellules, ce qui justifie la dénomination courante de liste chaînée.
Notons qu’il s’agit donc d’une structure linéaire, qu’on peut parcourir en partant du début, mais sans aucun accès direct à un élément autre que le premier.
Voici la représentation schématique d’une liste chaînée comportant, dans cet ordre, les trois éléments 1, 2 et 4 :

Le champ suivant de la dernière cellule renvoie vers une liste vide, conventionnellement nommée nil et représentée ci-dessus par un hachurage.
Bien que dans la figure ci-dessus les maillons soient présentés comme s’ils se suivaient en mémoire, il est très probable que ceux-ci soient éparpillés au travers des millions d’octets de la mémoire vive ( ils ne sont donc pas contigus )
Dans cette implémentation, une liste ( mais pas les valeurs stockées ! ) est donc définie entièrement par les champs valeur et suivant de sa première cellule ( que l'on appelle la tête de la liste ). C'est donc une définition récursive d'une liste : elle est égale à sa première valeur + la suite des éléments de la liste , qui elle-même est définie comme une valeur + une suite, etc....
La liste ci-dessus pourrait ainsi être définie par l'opération : liste = maillon(1, maillon(2, maillon(4, nil))).
| Avantages | Inconvénients |
|---|---|
|
|
ListeLa POO est bien adaptée à la création d'une liste chaînée. Pour implémenter le type LISTE sous forme de liste chaînée en POO, on peut utiliser deux classes distinctes :
Maillon d'attributs valeur et suivant; cette classe ne contient qu'un constructeur et aucune méthode :
class Maillon:
def __init__(self, valeur, suivant = None): # création d'un maillon qui ne pointe par défaut vers aucun autre
self.valeur = valeur
self.suivant = suivant # suivant est de type Maillon !
Le paramètre suivant contient le lien vers l'objet de type Maillon suivant dans la chaîne, ou None si il s'agit du dernier maillon.
Si on ne fournit pas d'argument suivant au constructeur, il est remplacé par défaut par None, ce qui permet donc de définir automatiquement le dernier maillon d'une liste.
Liste très simple :
class Liste:
def __init__(self, tete = None): # création liste, vide par défaut si aucun maillon n'est fourni en argument
self.tete = tete # stockage de sa tête. Le paramètre 'tete' est bien entendu de type Maillon !
Le seul attribut de la liste est donc son maillon de tête : initialement, ce peut être l'élément None ( liste vide ) par défaut, ou un maillon passé en paramètre..
Cette tête peut ensuite être "allongée" pour rajouter d'autres éléments ( = d'autres maillons ) dans la liste, mais la seule information directement accessible est donc bien uniquement cette tête.
Cependant, il ne faut pas croire que self.tete contient uniquement l'information du seul premier élément de la liste : elle contient en fait toute la structure de la liste,
c'est à dire les éléments eux-mêmes mais aussi les "liens" vers les maillons successifs.
L'intérêt de cette implémentation à deux classes est de pouvoir créer des listes vides; en effet, un Maillon égal
à None n'est pas la même chose qu'une Liste sans tête ( [] != [None] ) ...
Pour chaque exercice ci-dessous, écrire le code demandé et quelques instructions de test montrant son bon fonctionnement.
Vous pouvez déjà tester la classe en instanciant un objet liste chaînée vide, ou contenant quelques valeurs.
Comment faut-il procéder ?
Remarque : on rappelle que le None signalant la fin de la chaîne est "automatiquement" ajoutée en fin de liste par l'implémentation proposée ci-dessus.
Écrire une méthode is_empty qui renvoie True si la liste est vide, False sinon.
A laquelle des deux classes ci-dessus doit appartenir cette méthode ? Le résultat de quel test simple faut-il ici renvoyer ?
C'est un peu délicat dans l'ordre des opérations :
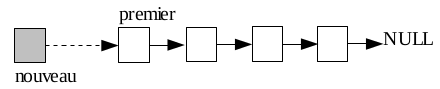
insert_first(valeur) qui ajoute un élément au début d'une liste chaînée.pop_first qui supprime un élément au début d'une liste chaînée. Cette méthode devra bien entendu
tester au préalable si la liste n'est pas vide !Pour ces primitives, il va être nécessaire de parcourir les éléments de la liste, soit en totalité, soit jusqu'à un certain élément.
Conformément à leur définition, les listes sont des structures récursives. Par conséquent, les opérations sur les listes s’expriment naturellement par des algorithmes récursifs.
En même temps, les listes ont des structures linéaires, parfaitement adaptées à un parcours itératif...
Vous allez donc dans un premier temps proposer des implémentations des méthodes suivantes de manière itérative, puis vous en donnerez ensuite une version récursive.
L'idée est de compter les éléments un par un en "traversant" la liste maillon après maillon, tant qu'on n'a pas atteint la fin de la liste : méthode len: maillon ← tete de la liste tant que l'on n'a pas atteint la fin de la liste: incrémenter un compteur maillon ← suite de la liste renvoyer la valeur du compteur
Pour "avancer d'un maillon" dans la liste, il suffit de "remplacer" le maillon courant par la suite de la liste ( c'est à dire son champ suivant ) !
__len__ qui renvoie le nombre d'éléments dans une liste chaînée, et qui permet d'utiliser la
syntaxe habituelle len(liste) pour déterminer le nombre d'éléments.Ou comment afficher le contenu de la liste ?
En vous inspirant de l'algorithme précédent, écrire la méthode spéciale __str__ qui retourne la liste ( sous forme de chaîne de caractères ) des valeurs stockées dans une liste chaînée.
Cette liste pourra alors être affichée afin de "visualiser" le contenu de la liste chaînée...
Utiliser ensuite cette méthode pour tester le bon fonctionnement de celles que vous avez écrites auparavant !
Écrire les méthodes spéciales __getitem__ et __setitem__ qui permettent respectivement le renvoi de la valeur d'un élément d'indice i, et l'affectation d'une valeur
à un élément d'indice indice.
Vous pouvez vous inspirer du code de la méthode précédente.
Les méthodes devront bien entendu gérer la situation où l'indice est "en dehors" de la liste ( IndexError ).
Dans ce cas :

append(valeur) qui ajoute un élément à la fin d'une liste chaînée. Cette méthode devra aussi gérer les deux situations, ajout à une liste vide ou non.Alors là, il faut vraiment bien réfléchir aux liens à mettre à jour...Voila le principe :
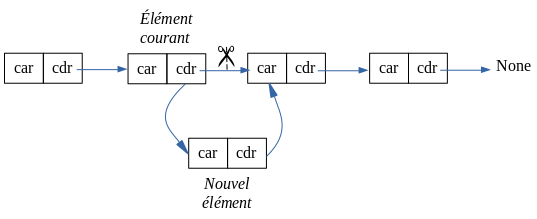
insert(indice, valeur) qui insère un élément à la position indice d'une liste chaînée.Attention à la manière de faire pour "s'arrêter" au "bon" indice d'insertion...
On peut remarquer que Python ne renvoie pas d'erreur si on essaye d'insérer une valeur à un indice en dehors de la taille d'une liste ( par exemple,
insert(5, 42) dans la liste [1, 2, 3]; dans ce cas, il effectue une insertion en fin de liste, donc l'équivalent d'un
append...
On pourra ici donner à la méthode insert le même comportement.
A vous de réfléchir, d'abord sur papier ( faites des schémas ! ), à l'ordre des opérations à faire pour :
Coder ensuite une méthode pop(indice), qui supprime l'élément de la liste à un indice quelconque, et qui renvoie la valeur de
l'élément supprimé.
Quelques indications :
nil; vers quoi alors ?? !On exploite ici le caractère récursif d'une liste chaînée.
Par exemple, pour le calcul du nombre d'éléments :
nil; on renvoie alors 0D'où l'algorithme :
fonction len(maillon: initialisé à la tête de la liste):
si maillon est nil: # on est arrivés en fin de liste
renvoyer 0
sinon:
renvoyer 1 + len(maillon.suivant)
Dans cette version, la méthode len prend donc un paramètre; on doit donc à son premier appel lui passer le premier maillon de la liste ( sa tête ) comme argument.
Pour un utilisateur, l'interface de cette fonction n'est donc pas très judicieuse...on peut remédier à cela en implémentant cette fonctionnalité sous la forme de deux fonctions :
class List:
def _len(self, maillon): # méthode "privée" ( le caractère underscore "_", non obligatoire, signale à l'utilisateur que cette fonction est "privée", donc à ne pas utiliser depuis l'extérieur )
..... # code de la méthode de traitement
def __len__(self): # méthode "publique" appelée par l'utilisateur
return _len(self.tete) # appel de la méthode "privée", et renvoi de son résultat
On peut ainsi appeler simplement la méthode len sans lui passer aucun paramètre, ce qui est son utilisation "normale" et attendue de la part d'un utilisateur !
Réécrire les méthodes précédentes de manière récursive; pour ne pas tout mélanger, on pourra travailler avec une autre classe, ListeRec par exemple.
Vous avez ( sûrement...) fait les exercices suivants avec des listes Python...vous allez maintenant les faire avec des listes chaînées !
Enregistrez le code des classes Liste ( et ListeRec ) et Maillon dans un fichier ( liste_chainee.py par exemple ), et importez ensuite le fichier pour
pouvoir l'utiliser dans les éditeurs ci-dessous ou avec Pyzo.
Vous pouvez pour les exercices suivants proposer des codes itératifs ou récursifs, au choix !
Écrire une fonctioncontient(liste, valeur), qui renvoie True si valeur se trouve dans la liste, False sinon.
Écrire une fonction py_to_linked(tab) qui prend pour paramètre une liste (un tableau) Python tab, et renvoie la liste chaînée correspondante.
Écrire une fonction occurrences(valeur, liste) renvoyant le nombre d’occurrences de valeur dans la liste chaînée liste.
Écrire une fonction renverse(liste) qui renvoie une nouvelle liste chaînée, inverse de la liste chaînée liste passée en paramètre.
Écrire une fonction concatene(l1, l2), qui prend deux listes chaînées l1 et l2 comme paramètres, et qui renvoie l1 à laquelle on a concaténé
l2 ( rôle de la méthode extend() de Python ).
Écrire une fonction insert_sort(liste, valeur) qui insère valeur dans la liste (supposée ordonnée) liste, de façon à ce que la liste reste ordonnée.
Attention, aucune vérification de l'ordonnancement initial de liste ne doit être effectué.
La liste sera modifiée par cette opération. La fonction renvoie la nouvelle valeur de la liste (indispensable si on insère en première position car la tête de liste change alors).
Attention :
En se servant de l'exercice précédent, écrire une fonction tri_insertion(liste) qui utilise cet algorithme pour trier la liste chaînée liste passée en argument.
Attention, cette liste ne doit pas être modifiée par cet appel, il faut retourner une nouvelle liste, triée.
A ne pas apprendre par cœur !
Une comparaison de la complexité en temps des trois implémentations de listes que vous avez vues :
| Opération | Liste par tableau statique | Liste par tableau dynamique | Liste chaînée |
|---|---|---|---|
| Accès à un élément | ?O(1) | ?O(1) | ?O(n) |
| Nombre d'éléments | ?O(1) | ?O(1) | ?O(n) |
| Insertion en tête | ?O(n) | ?O(n) | ?O(1) |
| Insertion à la fin | ?O(n) | ?O(1)* | ?O(n) |
| Insertion en n'importe quelle position | ?O(n) | ?O(n) | ?O(n) pour le premier élément inséré, ?O(1) pour les suivants |
| Suppression en tête | ?O(n) | ?O(n) | ?O(1) |
| Suppression en fin | ?O(n) | ?O(1)* | ?O(n) |
| Suppression en n'importe quelle position | ?O(n) | ?O(n) | ?O(n) pour le premier élément supprimé, ?O(1) pour les suivants |
* il s'agit en fait d'une complexité "amortie".
Selon le critère pour lequel un algorithme donné doit être le plus efficace, on choisira donc telle ou telle implémentation.
Le langage LISP a été inventé au MIT à la fin des années 50 par John McCarthy. On l'a beaucoup utilisé dans le domaine de l'intelligence artificielle, et il est encore employé de nos jours, notamment comme langage d'extension dans l'éditeur de texte Emacs ou l'outil de CAO AutoCAD.
De nombreux "dialectes" de ce langage existent; ils ont été "unifiés" au sein de Common Lisp, qui sera la version que nous utiliserons ici.
Le terme Lisp a été forgé à partir de l'anglais « list processing » (« traitement de listes ») : en effet, tout est manipulation de listes en Lisp !

LISP manipule des expressions sous forme :
Dans ce deuxième cas, Lisp considère toujours le premier élément comme une fonction, et évalue toujours le résultat de l'expression.
L'évaluation des expressions se fait de manière préfixe, c'est à dire les opérateurs de calcul en premier, puis les données :
>>> 3 ; une simple valeur
3
>>> nil ; l'équivalent de None ou de False
NIL
>>> t ; l'équivalent de True
T
>>> "Que de parenthèses..." ; une chaîne de caractère(s)
"Que de parenthèses..."
>>> (+ 2 3 8) ; somme de 3 nombres
11
>>> (- 5 6) ; différence
-1
>>> (* 6 8) ; produit
48
>>> (* 2 (cos 0) (+ 4 6))) ; expression plus complexe
20
Si on ne souhaite pas évaluer une expression, il faut la faire précéder d'un caractère quote '.
Notamment, c'est indispensable pour la définition d'une liste en tant que structure de données :
>>> '(1 5 6 78 9 41) ; définition d'une liste sans évaluation
(1 5 6 78 9 41)
Le premier élément 1 serait sinon considéré comme une fonction, ce qui générerait bien entendu une erreur...
Si vous rencontrez l'erreur : EVAL: XXX is not a function name; try using a symbol instead, pensez à cette particularité.
Au sein d'un programme, on peut utiliser l'instruction write pour afficher le résultat de l'évaluation d'une expression :
(write (/ 36 6)) ; affichage du résultat de l'évaluation de la division de 36 par 6
Même si on peut souvent s'en passer, Lisp permet l'affectation de variables avec la fonction setf :
(setf a 45) ; affectation de la valeur 45 à la variable 'a'
(setf l '(12 4 6 98 7 35)) ; affectation d'une liste à la variable 'l'
Lisp n'est pas sensible à la casse : liste et LISTE désigneront donc la même variable.
L'implémentation des listes en Lisp correspond à des listes chaînées ( même si en interne, c'est plutôt une structure d'arbre qui est utilisée ).
Une liste peut être :
nil)car ou first), suivi de la suite de la liste (cdr ou rest) terminé par nil.
>>> (first '(56 12 7 8 95))
56
>>> (rest '(56 12 7 8 95))
(12 7 8 95)
>>> '()
NIL
LISP dispose de la fonction cons pour construire une liste à partir d'un élément et d'une autre liste :
>>> (cons 1 '(2 3 4))
(1 2 3 4)
Lisp dispose de l'équivalent du if...else... , mais pas du elif ( il est donc nécessaire d'"imbriquer" logiquement différentes expressions conditionnelles )
(if (condition)
(résultat renvoyé si la condition est vraie)
(résultat renvoyé si elle est fausse)
)
Exemples de condition :
(if (= a 3) ; si a est égale à 3
...
)
(if (/= c 45) ; si c est différente de 45
...
)
(if (null l) ; si la liste l est vide ( = égale à nil )
...
)
Le mot-clé à utiliser est defun, suivi du nom de la fonction, puis de la liste du (ou des) paramètre(s) entre parenthèses :
(defun ma-fonction(a b)
expression 1
expression 2
....
)
L'appel de la fonction se fera avec une expression analogue à celle vue ci-dessus :
(ma-fonction 15 23) ; appel seul de la fonction
(write (ma-fonction 15 23)) ; appel et affichage du résultat renvoyé
Il est à noter que, comme chaque expression est évaluée par Lisp, c'est le résultat de la dernière expression évaluée qui est renvoyé en sortie de fonction : pas besoin de 'return'...
(defun plus-grand(a b)
(if (> a b)
a ; résultat renvoyé si la condition est vraie
b ; résultat renvoyé si elle est fausse
)
)
L'indentation du code lui apporte de la lisibilité, mais ne structure pas la logique du programme, contrairement à Python; elle n'est donc pas obligatoire.
Pour travailler les exercices, vous utiliserez :
produit qui calcule le produit de deux nombres passés en arguments; écrire l'instruction d'appel de la fonction, et afficher le résultat renvoyébissext qui détermine si l'année passée en argument est bissextile ou pas. Attention à la manière d'écrire la condition à tester !and et or sont les fonctions logiques analogues des opérateurs de mêmes noms
en Python. somme qui calcule la somme des entiers de 0 à N, valeur passée en argument à la fonction.somme-liste qui calcule la somme des éléments d'une listelen-liste qui calcule le nombre d'éléments dans une listeget-element qui affiche la valeur de l'élément en un indice quelconque d'une liste.