Piles

Un problème...

Avant d'évaluer le résultat d'une expression mathématique, les calculatrices vont déterminer d'abord l'ordre des opérations à effectuer sur les nombres rentrés.

Cet ordre est précisé par des signes comme des parenthèses '()', des crochets '[]' ou des accolades '{}'.

Pour qu'il n'y ait pas d’ambiguïté sur le calcul à faire, il faut que chaque symbole ouvrant possède son symbole fermant, et que les paires de symboles ouvrant+fermants soient correctement "imbriqués".
Par exemple :

{ [ (( )) ] } est correctement écrit
{ [ (( )) } ne l'est pas ( il manque un crochet fermant ).
{ [ () ]) ) } ne l'est pas ( parenthèses et crochets sont mal imbriqués ).

Quel est le moyen le plus efficace pour vérifier que ces conditions sont vérifiées ?

→ on pourrait compter le nombre de symboles de chaque type ouvrants, puis vérifier qu'il y en a autant de fermants.

Problème : ne permet pas de vérifier que l'imbrication est correcte...il faut en plus se souvenir de l'ordre dans lequel chaque symbole ouvrant est apparu.

Une solution

A chaque fois que l'on rencontre des symboles ouvrants, on les note, les uns à la suite des autres dans l'ordre dans lesquels ils apparaissent.

Quand on rencontre un symbole fermant, on vérifie qu'il correspond bien au dernier symbole ouvrant noté : si c'est le cas, on efface ce dernier de la liste et on continue le parcours de l'expression jusqu'à la fin.
Si ce n'est pas le cas, ou si l'on a atteint la fin de l'expression alors qu'il reste encore des symboles ouvrants dans la liste, il y a un problème...

La liste que l'on a utilisée pour stocker les symboles ouvrants nous a permis, en plus de stocker le nombre de ces derniers, de retenir directement l'ordre dans lesquels ils sont apparus dans l'expression, celui qui apparaissait en dernier étant le plus prioritaire à traiter.

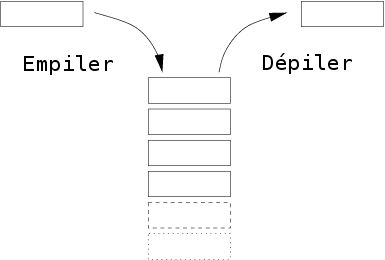
Une telle structure s'appelle une pile.

Principe d'une pile

Définition

En informatique, une pile (en anglais stack) est une manière d'organiser des données, fondée sur le principe « dernier arrivé, premier sorti » (ou LIFO pour Last In, First Out), ce qui veut dire que les derniers éléments ajoutés à la pile seront les premiers à être récupérés.

Le fonctionnement est donc celui d'une pile d'assiettes : on ajoute des assiettes sur la pile, et on les récupère dans l'ordre inverse, en commençant par la dernière ajoutée ( le "sommet" de la pile ).

Une pile est utile dans tous les cas où il faut mémoriser une information avant son traitement, la dernière information mémorisée étant celle à traiter en priorité.

Quelques applications des piles

Dans un navigateur web, une pile sert à mémoriser les pages Web visitées. L'adresse de chaque nouvelle page visitée est empilée et l'utilisateur dépile l'adresse de la page précédente en cliquant le bouton « Afficher la page précédente »
L'évaluation des expressions mathématiques ( exemple d'introduction ) ou la vérification des parenthèses/crochets/accolades par un langage de programmation
La fonction « Annuler la frappe » (en anglais « Undo ») d'un traitement de texte mémorise les modifications apportées au texte dans une pile.
Certains algorithmes utilisés sur les structures de données comme les arbres ou les graphes utilisent avec profit une pile pour mémoriser les nœuds visités.
Les algorithmes récursifs admis par certains langages utilisent implicitement une pile d'appel pour mémoriser les informations d'un appel récursif au suivant.

Ce qu'il faut pour faire une pile

Il faut d'abord réfléchir à la manière dont on va structurer les données d'une pile.

Le plus simple est de la voir comme un ensemble d'éléments, rangés dans un certain ordre, mais dont on n'aurait accès qu'à un "bout" ( le premier ou le dernier ), son "sommet".

Ensuite,il faut se poser la question : de quelles opérations doit-on disposer pour faire fonctionner la pile ?

Il n'y a en fait pas besoin de grand chose pour faire fonctionner une pile :

création d'une pile vide
"empiler" ( push en anglais ) un élément au sommet de la pile
"dépiler" ( pop en anglais ) l'élément au sommet de la pile
savoir si la pile est vide ou non ( en effet, on ne peut pas dépiler un élément d'une pile vide. )

On pourrait éventuellement, au besoin, ajouter d'autres opérations :

connaître la longueur ( nombre d'éléments ) de la pile
consulter ( sans le dépiler ! ) l'élément au sommet de la pile
....

Tout dépend de ce dont l'utilisateur a besoin pour faire fonctionner son code avec cette pile...

Comment coder une pile ?

En Python, et dans de très nombreux langages, la pile n'est pas une fonctionnalité disponible "de base" : il est souvent nécessaire de la coder soi-même...

Une idée vient tout de suite à l'esprit : représenter une pile à l'aide d'un tableau, dont le sommet sera le dernier élément, semble très bien convenir pour représenter une pile.

Dans tous les exercices suivants, on utilisera le paradigme orienté objet pour réaliser le travail demandé.

Version tableau de taille fixe

On va dans un premier temps considérer une pile dont la "capacité" est limitée à une certaine "taille" ( 10 "niveaux" par exemple ).
En effet, certains langages de bas niveau ne gèrent que ce genre de structure et il est intéressant de voir comment s'en tirer dans cette situation.

Et rappelez-vous la pile d'exécution Python qui ne permet que 100 niveaux de récursivité...

Codage

Écrire, et bien entendu tester, une classe PileStatique qui permettra la gestion d'une structure de données de type pile en utilisant un tableau de taille fixée ( 10 niveaux par exemple ).

Cette classe comprendra les méthodes suivantes :

création d'une pile vide. A l'initialisation, chaque niveau de la pile pourra par exemple contenir la donnée None.
savoir si la pile est vide ( méthode est_vide() ). La question est : comment repérer le niveau auquel correspond le sommet de la pile ?
empilage d'un élément ( méthode empiler() ). Il faut bien entendu qu'il reste "de la place" au sommet de la pile pour éviter un débordement de pile ( "stack overflow" )
dépilage d'un élément ( méthode depiler() ). La méthode devra bien entendu au préalable vérifier que la pile n'est pas vide ! Elle devra de plus renvoyer l'élément dépilé.

class PileStatique: pass

SOLUTION

Version tableau de taille variable

Codage

Écrire, et bien entendu tester, une classe PileDynamique qui permettra la gestion d'une structure de données de type pile en utilisant un tableau dynamique Python.

Cette classe comprendra les mêmes méthodes que la précédente.

class PileDynamique: pass

SOLUTION

Intérêt/inconvénients des différentes implémentations

Dans l'éditeur ci-dessous, indiquer, en justifiant, quels sont les avantages/inconvénients des deux implémentations du TAD PILE que vous venez de voir.

Quelle autre implémentation serait-il judicieux d'utiliser pour implémenter une pile ? Comment et pourquoi ?

AVANTAGES/INCONVÉNIENTS DE DIFFÉRENTES IMPLÉMENTATIONS DU TAD PILE 1. Tableau de taille fixe : 2. Tableau dynamique ( type list Python ) : 3. Autre implémentation judicieuse :

SOLUTION

Conclusion

Maintenant, nous pourrions mettre les deux classes précédentes dans un fichier nommé par exemple pile.py, que nous pourrions importer au début d'un script où nous aurions besoin d'une pile.


from pile import *

pile = PileStatique() # ou pile = PileDynamique()


pile.empiler(12)
pile.empiler(4)

s = pile.depiler()
.....

A part l'instruction d'instanciation de la pile, l'interface des deux classes serait exactement la même du point de vue de l'utilisateur.

Exercices et applications

Pour pouvoir utiliser les classes PileStatique et PileDynamique dans les éditeurs ci-dessous, pensez à charger au moins une fois le module pile.py avec le bouton Charger un module.

Dans votre script, pensez ensuite bien entendu à importer le module.

Inversion d'une pile

Écrire une fonction inversion_pile qui renvoie une pile inverse de celle passée en argument : le sommet de la première pile doit se retrouver "tout en bas" de la nouvelle pile, et inversement.

Attention, la pile passée en argument doit rester non modifiée à la fin de la fonction...

from pile import * def inversion_pile(pile): pass

SOLUTION

Inversion d'une chaîne de caractères

Écrire une fonction inversion_chaine utilisant une pile, qui retourne la chaîne passée en argument avec ses caractères dans l'ordre inverse :


>>> c1 = 'abcdefgh'
>>> print(inverse(c1))

'hgfedcba'

>>>

from pile import * def inversion_chaine(ch: str)->str: pass

SOLUTION

Maximum/minimum des éléments d'une pile

Écrire deux fonctions maximum_pile et minimum_pile qui détermine l'élément respectivement maximal et minimal d'une pile passée en argument.

La pile ne devra bien entendu pas avoir été modifiée après ces recherches...

from pile import * def maximum_pile(pile)->int: pass def minimum_pile(pile)->int: pass

SOLUTION

Copie d'une pile dans une autre

Écrire une fonction copie_pile qui retourne une nouvelle pile, copie de celle passée en argument.

La première pile doit là aussi rester non modifiée à l'issue de la copie...

from pile import * def copie_pile(pile): pass

SOLUTION

Simulation de la récursion avec une pile

On avait évoqué dans le cours sur la récursivité l'utilisation par Python d'une pile ( la pile d’exécution ) pour stocker les informations entre les différents appels d'une fonction récursive.

Bien que les informations stockées dans la "vraie" pile d'exécution soient multiples, nous allons essayer de simuler le fonctionnement d'une fonction récursive à l'aide d'une pile, qui ne contiendra que les valeurs passées comme paramètres, et les résultats renvoyés par les différents appels récursifs.

On utilise alors deux boucles successives :

la première, qui simule les différents appels récursifs : on empile dans ce cas les différents paramètres passés d'un appel à un autre
la deuxième, qui simule le renvoi des résultats d'un appel à l'autre, et qui réalise donc les calculs

Par exemple, reprenons la fonction d'introduction du cours sur la récursivité ( calcul de la somme des nombres de 1 à N ):


def sum_rec(N):
    if N == 1:
       return 1
    else:
        return N + sum_rec(N-1)

Voila un algorithme qui permet de simuler les appels récursifs/renvois de cette fonction :


fonction sum_stack: N
	pile ← pile vide
	
	# Boucle de simulation des appels récursifs :
	tant que N différent de 0:
		empiler(N, pile)
		N ← N - 1
		
	# Boucle de simulation des renvois
	tant que la pile n'est pas vide :
		resultat ← depiler(pile) + depiler(pile)
		empiler(resultat)	
		
	renvoyer resultat

La variable resultat contient les résultats intermédiaires calculés, et, en fin d'exécution, le résultat final renvoyé au programme principal.

On constate bien que l'on n'utilise que des primitives "autorisées" par le TAD PILE : empiler, depiler, et test si la pile est vide.

Faire la trace de l'exécution de ce programme en représentant le contenu de la pile à chaque étape de l’exécution.
Compléter la fonction Python ci-dessous qui implémente cet algorithme; pour vérifier votre réponse à la question précédente, afficher la pile à chaque étape de l'exécution.
écrire un script qui calcule la factorielle d'un nombre N.
écrire un script qui calcule la somme des éléments d'un tableau.

La structure try ... except ... ( hors programme ) utilisée ici permet d'éviter la levée d'une exception ( = erreur à l'exécution ) lorsque la pile est vide et qu'on cherche pourtant à dépiler; cela se produit car le code n'est pas protégé contre cette situation, mais on s'en fiche ici...😇

from pile import * def sum_stack(N): pile = ... while N != 0: ... N = N - 1 while ... : try: resultat = ... ... except: pass return resultat

SOLUTION

Vérification du parenthésage

Et on en vient à notre exemple du début...

Écrire une fonction check_parenth utilisant une pile, qui :

a comme paramètre une chaîne de caractères représentant une expression de calcul contenant des accolades, crochets ou parenthèses.
retourne True ou False selon que le parenthésage est correct ou non

Tester votre fonction avec le jeu de tests suivant :


check_parenth("{3*(2+[5/(6-x)])}") == True

check_parenth("5+3*{1-[2*(5/(6-x))]}") == True

check_parenth("{3*(2+[5/(6-x)]))") == False

check_parenth("{(3*(2+[5/(6-x]))}") == False

check_parenth("{3*(2+[5/(6-x)]))}") == False

Vous vous inspirerez de l'algorithme décrit en introduction de ce chapitre. Vous pourrez tester votre fonction à l'aide des expressions ci-dessus.

Réfléchissez bien à la manière de déterminer si un caractère de l'expression est un symbole ouvrant ou fermant, et ensuite, de pouvoir déterminer à l'aide de la pile si la correspondance ouvrant/fermant est correcte pour chaque paire de symboles.

Votre script ne s'intéressera pas aux autres caractères ( chiffres, opérateurs ) présents dans l’expression mais uniquement aux parenthèses, accolades et crochets.

Vous pourrez ensuite améliorer votre code en faisant en plus retourner à la fonction la position dans l'expression du symbole qui pose problème ( voire, pour les plus ambitieux, une copie de l'expression mettant en "surbrillance" ce symbole ).

from pile import * def check_parenth(exp: str)->bool: pass

SOLUTION

Ouverture à d'autres langages : FORTH

FORTH a été conçu vers la fin des années 60 par Charles H. MOORE. Celui-ci fut tellement satisfait du résultat de son œuvre qu'il voulut l'appeler langage de quatrième génération (FOURTH).
Mais la machine sur laquelle il avait développé son langage (un IBM 1130), n'acceptait que des noms de programmes de cinq lettres, ce qui lui fit choisir FORTH comme nom définitif.

FORTH se trouve implémenté dans de nombreux appareils électroniques industriels : microcontrôleurs, systèmes embarqués, systèmes de pesée pour les grands et lourds véhicules , automates de laboratoires, terminaux graphiques, tableaux de bord des navires, projecteurs cinématographiques, appareils d'hôpitaux, ... et grand public : autoradios numériques, robotiques de cuisine, broyeurs de café en grain, caisses enregistreuses, appareils de cuisson multifonctions, ...
Le socle technique bas niveau des "smart contracts" du célèbre Bitcoin ont été écrits en Forth, ainsi que de nombreuses actuelles solutions de contrôle du trafic aérien international.

Concepts de base

FORTH est construit autour de deux piles:

La Pile de données (DATA STACK)
La Pile de retour (RETURN STACK)

Exemple : quand vous entrez les nombres suivants ( suivis d'un appui sur la touche ENTREE ) :

    
1 5 7 6 ↩

L'interpréteur FORTH analyse le flot d'entrée (en FORTH, l'espace est l'unique séparateur d'instructions reconnu), et quand il reconnaît un nombre, empile celui-ci sur la pile de données.
Après analyse de la ligne précédente, la pile de données a l'aspect suivant:

1 5 7 6 ← sommet de la pile

Calculs

FORTH utilise la notation dite RPN (Reverse Polish Notation, Notation Polonaise Inversée), très utilisée par les calculatrices du type Hewlet Packard, entre autre.

Ce type de notation s'exécute toujours de gauche à droite ( notation suffixe ).
Elle permet d'éliminer la notion de hiérarchie des opérateurs, courante dans la plupart des langages de programmation traditionnels, et qui spécifie l'ordre d'exécution de ceux-ci (* avant /, + avant -, etc...), en utilisant au besoin des parenthèses, qui deviennent inutiles ici.

En FORTH, l'application de ce principe se fait de la façon suivante :

les opérandes ( données ) sont empilés au fur et à mesure de leur rencontre
les opérateurs sont exécutés immédiatement. Il opèrent sur les derniers opérandes empilés, qui sont alors supprimés de la pile de données; le résultat de l'opération est empilé à leur place, et pourra à son tour servir d'opérande.

Exemple : l'expression (2 + 5) * 3 s'écrira en Forth :

2 5 + 3 *

A l'aide du simulateur ci-dessous, calculer en Forth le résultat des expressions ( et vérifiez bien sûr que vous obtenez le résultat correct ! ).
La première ligne du simulateur donne l'état actuel de la pile de données.

2 + (3*5)
1 - 12 / ( 4 + 2 )
((2+5) * (7-2)) / ((4+3) * 5)

Référence du simulateur utilisé : Easy Forth.

SOLUTION

Manipulation des piles

dup : duplique au sommet de la pile l'élément au sommet :
```
1 2 6 9 13
dup 
1 2 6 9 13 13				
				
```
drop : supprime l'élément au sommet de la pile
```
1 2 6 9 13 13
drop
1 2 6 9 13				
				
```
over : duplique au sommet de la pile l'avant-dernier élément au sommet :
```
1 2 6 9 13
over
1 2 6 9 13 9				
				
```
swap : échange les deux éléments au sommet de la pile :
```
1 2 6 9 13 9
swap
1 2 6 9 9 13				
				
```
rot : effectue une rotation vers le bas de la pile des 3 éléments au sommet de la pile ( -rot pour une rotation vers le haut ) :
```
1 2 6 9 9 13
rot
1 2 6 9 13 9				
				
```
>r : dépile le somme de la pile de données vers la pile de retour ( r> pour l'opération inverse )

A l'aide de ces commandes, faites le tri de la pile ci-dessous :

3 2 4 1 6 5

→ 1 2 3 4 5 6

SOLUTION

Sortie vers la console

. : dépile le sommet de la pile de données et l'affiche
.s : affiche le contenu complet de la pile ( sans la dépiler )
cr : retour à la ligne
XX emit : affiche le caractère dont le code ASCII est XX
." Chaîne" : affiche une chaîne de caractères ( ne pas oublier l'espace après les guillemets )

"Fonctions" en Forth

La notion de fonction n'existe pas en Forth : il n'y a pas possibilité qu'un morceau de code "renvoie" un résultat à un "programme principal".
L'équivalent le plus proche est la définition de mots qui viennent "enrichir" le vocabulaire de base de Forth, et qui pourront ensuite être réutilisés.

Voila par exemple la définition d'un mot élevant au carré un nombre, et son utilisation :

la définition d'un mot commence par deux points :, suivi du nom du mot ( séparé bien entendu par un espace ! )
viennent ensuite les mots permettant de réaliser l'action associé au nouveau mot
la définition se termine par un point-virgule ; ( précédé d'un espace ! )
l'utilisation du mot peut se faire alors de manière analogue à précédemment, en empilant le résultat de l'action ( carré de 5 ci-dessus ), ou en l'affichant ( carré de 11 ).

Ici, l'action du mot carre est de dupliquer le sommet de la pile ( dup ), et de multiplier les deux éléments au sommet ( qui sont donc identiques, on obtient le carré ).

Écrire la définition des mots Forth suivants, puis les utiliser pour tester leur bon fonctionnement :

somme : réalise la somme de deux nombres.
fahrenheit : convertit une température des ° celsius vers les ° fahrenheit ( °F = 1,8 x °C + 32 )
volume: calcule le volume d'un parallélépipède ( V = Longueur x largeur x hauteur )

SOLUTION

Structures de contrôle

Conditions

La structure conditionnelle ne peut en Forth être utilisée que dans la définition d'un mot.

La syntaxe est la suivante :


( condition ) if ( si VRAI ) else ( si FAUX ) then

La condition à tester doit bien entendu être écrite dans l'ordre suffixe :


3 4 = ( équivalent de 3 == 4 ? ) 
3 4 > ( 3 > 4 ? )
3 4 <	( 3 < 4 ? )

A noter : l'équivalent de True en Forth est 0, et celui de False est -1.

On peut utiliser les mots and, or et invert pour exprimer la condition :


3 4 < 20 30 < and ( 3 < 4 and 20 < 30 ? )
3 4 < 20 30 > or ( 3 < 4 or 20 > 30 )
3 4 < invert ( not (3 < 4) )

Tout ce qui est entre les mots if et else correspondent aux actions si la condition est vraie, et tout ce qui est entre les mots else et then aux actions si la condition est fausse.

Exemple : un mot est-pair? ( par convention, un mot conditionnel se termine par un point d'interrogation ?) qui teste si la valeur au sommet de la pile est multiple de 2 ou pas :

Définir un mot bissext qui détermine si l'année placée au sommet de la pile est bissextile ou pas ( plusieurs manières de faire. Pas facile...)

SOLUTION

Boucles

La structure do ... loop est l'équivalent aussi bien de la boucle for ... in range ....

Comme l'évaluation de condition, cette structure ne peut s'utiliser que dans la définition d'un mot.


(borne supérieure) (borne inférieure) do (actions à répéter) loop ;

Les deux bornes sont dépilées au début de la boucle; à l'intérieur de la boucle, le mot spécial i permet d'empiler l'index du compteur de boucle.

Exemple : un code qui affiche les entiers de 1 à 11 :

Comme le range de Python, l'index de la boucle ne va que jusqu'à la borne supérieure moins le pas ( qui est de 1 par défaut ).

définir un mot boucle qui permette d'afficher les nombres entiers entre n'importe quelles bornes, empilées au sommet de la pile.
définir un mot table-3 qui affiche tous les multiples de 3 de 3 x 1 à 3 x 10
définir un mot table-n qui affiche tous les multiples de n de n x 1 à n x 10.

SOLUTION