TP Diviser pour Régner 2 : les deux points les plus proches

Nous allons nous intéresser ici au problème suivant : étant donné un ensemble de points du plan, identifier le couple de points les plus proches.
Ce type d’algorithme a son utilité dans les transports aériens ou maritimes par exemple ( ou de manière plus anecdotique, dans la gestion des rebonds dans le TP que vous avez fait en introduction du cours sur la POO...)

Structures de données utilisées

Nous représenterons un point par un tuple de deux entiers correspondant aux coordonnées cartésiennes (x, y) du point dans un repère orthonormé.

L’ensemble des points considérés sera quant à lui stocké dans un tableau t. Nous supposerons toujours que tous les couples stockés dans t sont distincts.

Une première solution

Distance entre deux points

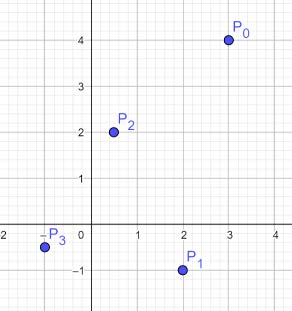
Considérons deux points P₁(x₁, y₁) et P₂(x₂, y₂); leur distance dite euclidienne est donnée par la relation : d_P1P2 = √(x₂ − x₁ )² + (y₂ − y₁)².

Écrire une fonction distance_euclidienne qui calcule la distance euclidienne séparant deux points.

def distance_euclidienne(p1 : tuple, p2: tuple)->float: pass

SOLUTION

Recherche naïve

Une méthode « naïve » permettant de déterminer les deux points les plus proches dans un tableau t consiste à considérer successivement tous les couples de points possibles, ce qui peut se faire facilement à l’aide de deux boucles imbriquées.

Écrire une fonction plus_proches qui prend comme paramètre un tableau de points t et renvoie les points (x1, y1), (x2 , y2) situés à la distance minimale l’un de l’autre, ainsi que cette distance.

Tester la fonction avec le tableau suivant :


plus_proches([(3, 4), (2, -1), (0.5, 2), (3, -4), (-1, -0.5), (-2, 5)]) == (0.5, 2), (-1, -0.5), 2.9154759474226504

Évaluer le coût d’un appel à la fonction plus_proches en fonction de la taille n du tableau t; en déduire la complexité de cet algorithme.

def plus_proches(t: list)->(tuple, tuple, float): pass return p1, p2, dmin

SOLUTION

Approche diviser pour régner

Nous allons maintenant nous intéresser à la mise au point d’un algorithme permettant de résoudre ce même problème en complexité O(n log n).

Idée de l'algorithme

On appelle P l'ensemble des n points à considérer.

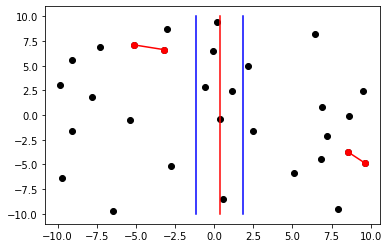
On partage P verticalement en deux sous-ensembles A et B de même taille ( ligne rouge sur l'image ci-contre ); la plus petite distance entre deux points de P est alors celle, soit entre deux points de A, soit entre deux points de B, soit entre un point de A et un point de B.

On calcule alors récursivement la distance minimale d_A entre deux points de A ( en rouge à gauche ) et la distance minimale d_B entre deux points de B ( en rouge à droite ); on note δ le minimum entre d_A et d_B.

Il reste alors à calculer la distance minimale entre un point de A et un point de B, ce qui laisse beaucoup de combinaisons...
Mais on réduit en fait les possibilités en écartant toutes les distances supérieures à δ : pour cela, on ne s’intéresse donc qu'aux points situés dans la bande verticale de largeur 2δ de part et d'autre du milieu de P ( lignes bleues sur la figure ).

Déroulement de l'algorithme

Diviser : on partage récursivement P en deux sous-ensembles A et B de même taille ( à un élément près ), de façon à ce que A contiennent les points de plus petites abscisses et B les points de plus grandes abscisses par rapport à une abscisse "milieu".
Dans la pratique, on construira A et B en divisant directement en deux parties le tableau des points préalablement trié par abscisses croissantes.
Régner : c'est le cas de base de la récursion; si n ≤ 3 ( c'est à dire si l'ensemble des points A ou B ne contient plus que 2 points au minimum ), on effectue une recherche naïve des points les plus proches dans A ( ou dans B ) : on renvoie d_A ( ou d_B ) ainsi que les deux points correspondants à cette distance minimale.
Combiner : c'est l'étape la plus délicate...
- on détermine le minimum δ entre les valeurs de d_A et d_B, et on stocke les deux points correspondants soit à d_A, soit à d_B.
- On sélectionne l’ensemble des points dont l’abscisse appartient à l’intervalle ]n//2 - δ , n//2 + δ[ ( bande délimitée par les lignes bleues ).
  Le plus simple pour la suite est de partir d'un tableau des points triés cette fois par ordonnées croissantes, dans lequel on sélectionnera l'ensemble des points à considérer.
- Pour chaque point de cette bande, on calcule les distances entre le point et les 7 points qui le suivent dans l'ensemble sélectionné ( donc ceux d'ordonnée supérieure ); on note δ' la plus petite de toutes ces 6 distances.
- On renvoie alors le minimum entre δ et δ', et les deux points correspondants.

Pas évident l'étape combiner !!!

Pourquoi ne considère-t-on que les points qui suivent un point donné ( ordonnée supérieure ) et pas ceux qui le précèdent ( ordonnée inférieure ) ?
Pour chaque point P_i de la bande, on ne considère que les points P_j situés au-dessus afin tout simplement de ne pas considérer chaque paire deux fois : P_i, P_j et P_j, P_i.
Pourquoi se contente-t-on de 7 points ?

Pour chaque point, on considère le rectangle s’appuyant sur les lignes bleues, dont le côté inférieur passe par le point, et de hauteur δ ( et de largeur 2δ).
S’il existe un point à une distance inférieure à δ du point, alors il est forcément dans ce rectangle.
Si on divise ce rectangle en huit carrés de côté δ/2, alors il ne peut y avoir au plus qu’un point par carré : en effet, s’il y avait deux points ( ou plus ) dans un carré, alors ces points seraient du même côté de la ligne rouge, donc tous les deux dans A ou dans B, et à une distance inférieure à δ/2, ce qui est impossible puisque δ est la distance minimale entre deux points de A ou deux points de B.
Il y a donc forcément 8 points au maximum dans le rectangle, le point considéré et 7 autres; il suffit donc effectivement de tester les 7 points suivants le point considéré, car tous les autres sont forcément en dehors du rectangle, et donc à une distance supérieure à δ...

Tableaux triés

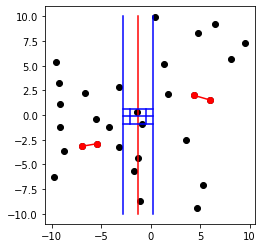
L'algorithme nécessite de disposer de deux copies du tableau t, l’une triée par abscisses croissantes et l’autre par ordonnées croissantes.

Écrire une fonction tri_x qui prend en paramètre le tableau t, et qui renvoie un nouveau tableau des points triés par abscisses croissantes.
Pour l'algorithme de tri à utiliser, on choisira...le plus efficace 😏 !...
Faire de même pour une fonction tri_y qui renvoie un tableau des points triés par ordonnées croissantes.

def tri_x(t: list)->list: pass def tri_y(t: list)->list: pass

SOLUTION

Implémentation de l'algorithme

Le travail à faire ci-dessous vous propose 3 niveaux de difficulté décroissante ( ***, ** et * ) pour implémenter cet algorithme pas du tout évident...

A vous de choisir la difficulté qui vous convient.

NIVEAU ***

Compléter la fonction plus_proches_dpr ci-dessous de façon à implémenter l'algorithme décrit précédemment. Attention aux paramètres et aux résultats renvoyés par cette fonction.

Cette fonction fera appel à celles que vous aurez écrites auparavant.

Pour la construction des différents tableaux, on aura bien entendu intérêt à utiliser des méthodes par compréhension.

NIVEAU **

Compléter la fonction plus_proches_dpr ci-dessous de façon à implémenter l'algorithme décrit précédemment. Attention aux paramètres et aux résultats renvoyés par cette fonction.

Cette fonction fera appel à celles que vous aurez écrites auparavant.

Pour la construction des différents tableaux, on aura bien entendu intérêt à utiliser des méthodes par compréhension.

def plus_proches_dpr(Px: list, Py: list)->(tuple, tuple, float): """Fonction implémentant l'algorithme de recherche de deux points les plus proches dans un ensemble de points. Entrées : Px = tableau des points triés par abscisses croissantes Py = tableau des points triés par ordonnées croissantes Sorties : p1, p2 = les deux points les plus proches d = la distance entre eux """ n = len(Px) # nombre de points # Cas de base : renvoi des points les plus proches dans A ( ou B ) et de dA ( ou dB ) if n <= 3: return ... # Construction des tableaux des points de A et de B : m = n//2 A = ... B = ... # Appel récursif de la fonction sur A et B, et récupération des résultats renvoyés : A1, A2, dA = ... B1, B2, dB = ... # détermination de d ( delta ) et des points correspondant de A ou de B : if dA < dB: p1 = ... p2 = ... d = ... else: p1 = ... p2 = ... d = ... # Construction du tableau des points appartenant à la bande verticale à considérer ( pas évident, attention ! ) : Q = ... # Calcul des distances entre les points de cette bande et les 7 suivants dans le tableau Q : for i in range(...): # pour chaque point de Q for j in range(...): # pour chacun des 7 points suivants ( attention aux bornes de la boucle !! ) dmin = ... # distance entre les deux points if dmin < d: # si cette distance est plus petite que d, p1 = ... # alors on modifie les informations stockées p2 = ... # sur les points les plus proches d = ... # et la distance minimale return ... # renvoi des deux points les plus proches et de la distance minimale

NIVEAU *

En déplaçant les lignes dans le code ci-dessous, reconstruire l'implémentation correcte de l'algorithme présenté précédemment.

SOLUTION

Test de la fonction

Tester le bon fonctionnement de la fonction plus_proches_dpr :

avec le tableau t utilisé pour le test de la version naïve
avec le résultat renvoyé par une fonction permettant de construire un tableau de n tuples (x, y) générés aléatoirement.

SOLUTION

Comparaison des deux algorithmes

Avec le tableau t, il n'y aucune différence dans le temps d’exécution des deux versions de la recherche, voire même l'approche DpR est plus lente à cause de ses multiples appels récursifs que l'on ne trouve pas dans la version naïve.

Mais comme d'habitude, la différence de complexité devient notable pour de grandes valeurs de n.

En utilisant le module timeit, comparer le temps d'exécution des deux versions de la recherche des deux points les plus proches.