
| longueur | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| prix | 0 | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |

L'objectif est donc de découper chaque planche de façon optimale pour en tirer un prix maximum.
Afin de bien appréhender le problème répondez aux questions ci dessous ( approche "par force brute" : on étudie TOUTES les possibilités, afin de déterminer la solution optimale :
Nous allons tenter de coder une fonction coupe_recurs prenant comme paramètres la longueur n de la planche et le tableau p
des prix, et qui renverra le revenu optimal que l'on peut tirer de la planche.
p[i] et de coupe_recurs(p, n-i) ?
3. Si l'on appelle q le revenu optimal d'une précédente hypothèse, comment
choisir entre q et la réponse à la question 2 de façon optimale ?
4. Déduire des questions précédentes un algorithme récursif résolvant le problème :
Coder alors cet algorithme :
Comme d'habitude, la solution récursive est "simple" à coder mais n'est pas très efficace...
Nous pouvons constater que nous sommes en présence d'un problème d'optimisation.
Nous allons maintenant chercher les sous problèmes et leurs chevauchements.
Nous allons maintenant tenter de construire un algorithme de résolution de ce problème grâce à la programmation dynamique, en se basant sur le code récursif précédent
Adapter le code récursif en vous inspirant de la fonction fibonacciProgDyna vue précédemment :
r[i] du tableau r contiendra les revenus maximum pour une planche de longueur iLa réflexion issue de la programmation dynamique consiste, comme vous avez pu le voir jusque là, à supprimer des calculs redondants.
Nous avons vu qu'une solution consiste à mémoïser (stocker dans une structure de données adaptée) les calculs réalisés dans une fonction récursive.
Mais la programmation dynamique ne s'appuie pas nécessairement sur la programmation récursive !
On peut aussi tout simplement raisonner plus classiquement : de façon itérative.
Dans le cas du problème de la planche, on peut :
Dans les deux cas on évite des calculs redondants en stockant chaque résultat intermédiaire.
Vous devez maintenant coder la fonction dyna_coupe_BU(n, p) permettant de résoudre le problème de façon dynamique en "Bottom-Up"
(d'où le BU).
Pour cela vous pouvez vous aider de l'ébauche algorithmique suivante :
n est la longueur de la planche
p est le tableau contenant les prix de chaque planche (p[i] est le prix de la planche de longueur i)
r est un tableau de longueur n+1 contenant initialement des 0
boucle i pour calculer le revenu optimal d'une planche de longueur i (i de 1 à n)
initialiser q
boucle j pour tester toutes les découpes pour la planche de longueur i (j de 1 à i : on réalise une découpe de longueur j<i)
q reçoit le maximum entre : une découpe précédente et ce que rapporte la découpe de longueur j
stocker le revenu d'une découpe i dans le tableau r
renvoyer le résultat
Vous avez déjà vu ce problème en première lors de l'étude des algorithmes gloutons.
Le rendu de monnaie est un problème du quotidien; la question est la suivante :
vous devez rendre 4,24€ avec un système de pièces et de billets donnés en minimisant le nombre de pièce ou billets rendus.
Vous avez déjà résolu ce problème de nombreuses fois, en suivant un algorithme "instinctif".
Nous allons essayer de généraliser la résolution de ce problème à n'importe quelle somme (bien sûr), et à n'importe quel système de pièces
et de billets.
Le problème du rendu de monnaie c'est :
monnaie=[pièce1, pièce2, ..., billet1, billet2, ...]Le problème consiste aussi bien sur à optimiser le rendu de monnaie en utilisant le moins de pièces ou de billets.
Lorsque que vous avez résolu ce problème en jouant au marchand dans votre enfance, ou l'année dernière en Première, vous utilisez classiquement l'algorithme glouton.
Un algorithme glouton est un algorithme qui fait un choix local optimal en espérant que cela conduise à une solution globale optimale.
Concrètement dans le cas du rendu de monnaie, on choisit toujours la pièce ou le billet le plus grand possible, puis on soustrait cette valeur à la somme à rendre et on recommence (en espérant rendre ainsi le moins de pièce ou de billets possibles !).
Dans le cas où le jeu de monnaie est le jeu européen actuel (le choix des valeurs des pièces et des billets n’a pas été fait au hasard), la solution gloutonne est optimale.
Mais nous pouvons imaginer un système dans lequel le rendu de monnaie glouton n'est pas optimal;
par exemple si l'on veut rendre 6 dans un système composé de [1,3,4] :
Pour fixer les idées nous allons nous poser un problème simple :
nous allons imaginer que nous disposons d'un système de pièces limitées : 2 cts, 5 cts, 10 cts, 50 cts et 1 euro (100 cts)
Nous voyons donc que la solution gloutonne n'est pas forcément optimale, il peut même arriver qu'elle ne trouve pas de solution.
Si l'on explore toutes les possibilités de l'exemple précédent ( rendu de 11cts ), on arrive à l'arbre ci-dessous :
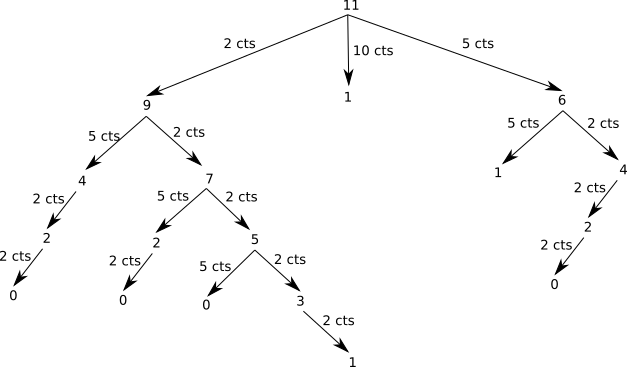
Une des solutions serait donc d'explorer de manière exhaustive toutes les branches de cet arbre, puis de sélectionner la ou les branches optimales.
La solution exhaustive est qualifiée de "force brute" car on parcourt toutes les solutions possibles avant de choisir la bonne.
Voici une fonction qui résout de façon récursive le problème du rendu de monnaie. La fonction renvoie le nombre de pièce optimal et non le rendu de monnaie lui même.
Le principe est le suivant : si l'on choisit une pièce de valeur x dans le système monétaire, il faut ensuite rendre la monnaie
sur somme-x et choisir le nombre de pièce(s) optimal ( le plus petit ) dans chaque cas.
Nous allons maintenant tenter d'optimiser cette fonction récursive grâce à la programmation dynamique.
Si l'on continue à analyser, on peut trouver dans cet arbre, des chevauchements de sous problèmes :

On se retrouve 2 fois à calculer comment rendre 4cts dans cette situation. on retrouve donc les conditions de la programmation dynamique avec :
rendu_dyna, qui prend en argument une somme à rendre et un tableau de systemede monnaie.somme+1rendu_dyna_memo(somme, systeme, f)Comme vous l'avez compris, nous venons de créer le tableau de mémoïsation f.
Par suite, ce tableau contiendra, à un indice i, le nombre de pièces à rendre pour la somme i.
Il nous reste à coder la fonction dyna_rendu_memo(somme, systeme, f) en s'appuyant sur la fonction récursive pure précédente.
Reprenez le code de votre fonction récursive et modifiez là comme indiqué ci-dessous :
f[somme] n'existe pas déjà dans le tableau.f[somme]Si vous avez suivi cette démarche pas à pas, vous voyez maintenant l'amélioration algorithmique qu'il existe entre une fonction récursive "simple" et une fonction récursive avec mémoïsation (programmation dynamique de haut en bas).
Question subsidiaire : pouvez-vous améliorer votre code pour qu'il renvoie aussi la liste des pièces à rendre pour la solution optimale ?
Ce problème classique de l'informatique est extrait du site https://projecteuler.net.
Le problème consiste à trouver le "chemin de poids le plus faible" dans une matrice, appelé "plus court chemin".

Les règles sont les suivantes :
L'objectif est de trouver le chemin le plus court en respectant ces règles.
Dans le tableau précédent, ce parcours est indiqué en rouge, et vaut : 131+201+96+342+746+422+121+37+331=2427.
Un algorithme glouton donnerait-il la solution optimale ?
Comme précédemment, nous allons chercher la relation de récurrence qui permet d'explorer toutes les possibilités de chemin afin de trouver celui de
poids le plus petit.
L'idée est de déterminer le chemin de poids minimal pour arriver à une case donnée tab[i][j], en fonction des cases depuis lesquelles on
vient dans le parcours.
Attention, plusieurs cas sont à considérer selon la situation d'une case dans le tableau : il y a deux cas particuliers, les cases tout
à gauche ( première colonne ) ou tout en haut ( première ligne ) du tableau
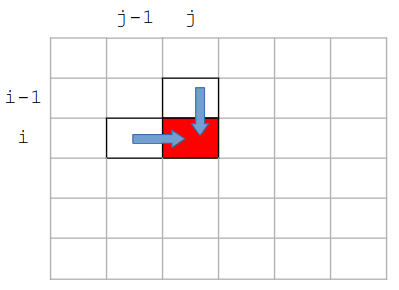
Écrire alors la fonction récursive qui implémente cet algorithme; vous pouvez la tester sur la matrice donnée en exemple ( attention à l'appel de la fonction : quelles valeurs doivent avoir les arguments de i et j ? )
Mais qu'en serait-il avec cette matrice de 80x80 ??? (N'essayez même pas...)
Nous allons tenter de résoudre ce problème grâce à la programmation dynamique.
Vous trouverez ci-dessous un peu de code permettant de transférer le fichier texte fourni
dans une liste de listes ( penser à enregistrer ce fichier sur votre PC, puis à le charger dans l'éditeur )
En vous inspirant des exemples traités précédemment, implémenter une version dynamique par mémoïsation de la fonction de recherche du chemin de poids
minimal. Vous utiliserez ici un tableau de tableaux phi de mêmes dimensions que la matrice, et ne contenant initialement que des
valeurs -1 ( par exemple ); ce tableau contiendra, si il a déjà été calculé, le poids du plus court chemin jusqu'à la case [i][j].
Tester votre code avec la matrice donnée en exemple, puis avec la matrice 80x80 : le résultat est alors 427 337.
Dans cette approche, on remplit le tableau phi depuis la première case (m[0][0]), en calculant pour chaque case le poids du plus court chemin pour
arriver jusqu'ici.
Attention là aussi aux cas particuliers à gérer ( première ligne et première colonne).
Le résultat sera obtenu en renvoyant la valeur stockée dans la dernière case du tableau de tableaux phi.
nxn contient aléatoirement répartis des pixels noirs.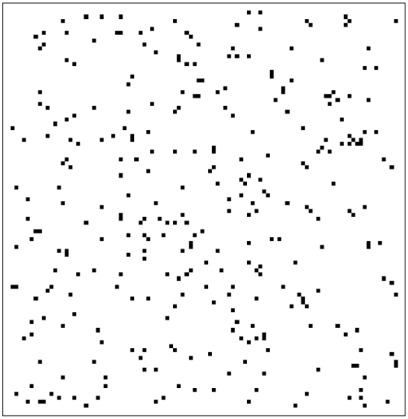
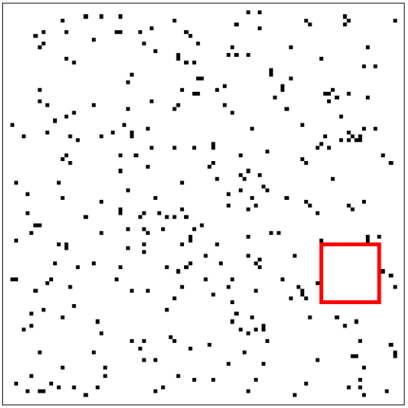
(x,y) la taille du plus grand carré blanc dont le pixel (x,y) est le coin en bas à droite.
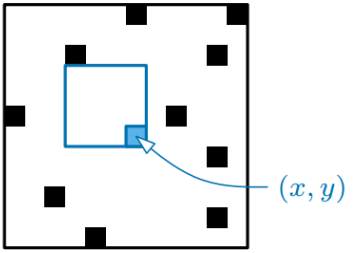
(i,i) (dont le coin en haut à gauche a pour coordonnées ((x+i,y+i))sont blancs, dès que l'on trouve un pixel noir, on arrête et on note les dimensions du carré précédent.mxm il faut vérifier m2 pixels.mxm est bien blanc, il suffit de vérifier si :
(m-1)x(m-1) représentés ci-dessous sont bien blancs
(x,y) placé en bas à droite de ce carré : plusGrdCarreBlanc(x,y,img).
plusGrdCarreBlanc(x,y,img) grâce à trois appels récursifs et à une fonction de recherche de minimum.plusGrdCarreBlanc(x,y,img)
test = [[1, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1]]

from random import randint
def creerIMG(n):
img=[[0 for i in range (n)] for j in range(n)]
for i in range(n):
x=randint(0,n-1)
y=randint(0,n-1)
img[x][y]=1
return img
memo contiendra dans la case [x][y] le plus grand carré blanc en partant du pixel en bas à droite.memomemo rempli initialement de None, et appeler ensuite la fonction récursive elle même.La distance d'édition (ou distance de Levenstein ou distance d'Ulam) est un algorithme permettant de comparer deux chaînes de caractères ch1 et ch2.
Cette distance est définie comme le nombre d'opérations minimum qui permet de passer de la première chaîne à la seconde en ne considérant que trois seules opérations possibles pour passer d'une chaîne à l'autre :
Par exemple :
Cet algorithme est utilisé de manière intensive dans les situations où il faut évaluer les différences entre un mot ou un texte, et un autre :
diff )On suppose ici que toutes les modifications ont un coût ( c'est à dire qu'elles augmentent la distance ) de 1.
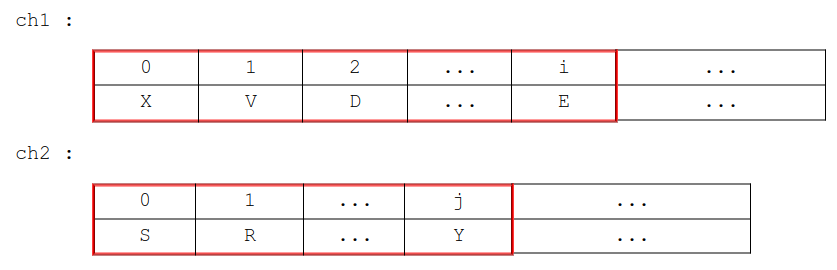
L'idée de l'algorithme dans sa version "naïve" est de déterminer les valeurs de distance entre toutes les sous-chaînes de ch1 et ch2.
d(i, j) la distance entre la sous-chaîne de ch1 d'indice 0 à i ( = "sous-chaîne i" ), et la sous-chaîne de ch2
d'indices 0 à j ( = "sous-chaîne j" ) :
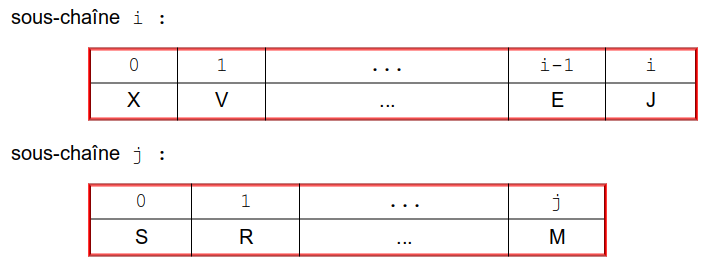
i == -1 ou j == -1 signifie que l'on considère une chaîne vide.d(-1, -1) = 0 ( la distance entre deux chaînes vides est la même qu'entre deux chaînes identiques, à savoir 0 ).d(-1, j) = j+1( la distance entre une chaîne vide et une chaîne contenant j+1 caractères ( les indices commencent à 0 ! ) est égale à j+1d(i, -1) = i+1 (idem )On compare les sous-chaînes de ch1 et ch2 pour 0 ⩽ i < len(ch1) et 0 ⩽ j < len(ch2).
Pour chaque comparaison, d(i, j) sera alors le minimum entre les valeurs de distance après chaque modification possible pour passer de la sous-chaîne i à la sous-chaîne j.
Analysons les cas possibles :

d(i, j) = 1 + d(i, j-1)
d(i, j) à la valeur de d calculée à l'appel précédent.
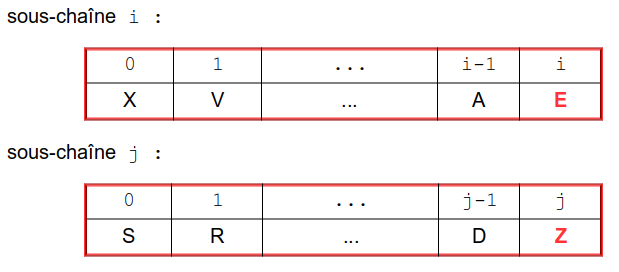
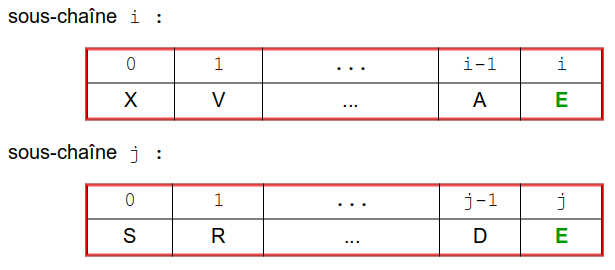
d(i, j) dans ces deux situations.
Compléter la fonction dist_lev_rec récursive ci-dessous qui prend en paramètre deux indices i et j, et qui renvoie
la distance de Levenshtein entre deux chaînes ch1 ( paramètre i ) et ch2 ( paramètre j ).
Pour simplifier la signature de la fonction ( il faudrait sinon aussi les passer en paramètres...), les chaînes ch1 et ch2 sont stockées dans deux variables définies dans le programme principal, et donc accessibles en lecture seule depuis la fonction.
Vérifier la correction de la fonction avec les exemples suivants, et d'autres !
On montre que la complexité de l'algorithme naïf est O(3(m+n)) ( où m et n sont les tailles des deux chaînes ) ! Pour comparer deux mots, c'est encore envisageable, mais pour comparer deux textes, cela devient inutilisable...
Essayez par exemple ( ou pas.. ) avec les deux phrases suivantes :
ch1 = "les sanglots longs des violons de l'automne blessent mon coeur d'une langueur monotone."
ch2 = "les sangliers lents des violents de l'atome blasent mon corps d'une longueur manhattan."
On doit trouver 21...
L'idée sera donc bien sûr de faire appel à la mémoïsation pour stocker les résultats déjà calculés à un appel récursif précédent, et de les réutiliser au besoin.
Ici, il faudra stocker ces résultats dans un dictionnaire, dont les clés seront les tuples (i, j) et les valeurs, celles des d(i, j) correspondant.
Comment initialiser ce dictionnaire ? Comment savoir si un résultat avait déjà été calculé ?
Écrire une fonction dist_lev_TB qui utilise la mémoïsation pour améliorer la complexité de l'algorithme :
Tester cette nouvelle version, notamment avec l'exemple des deux phrases ci-dessus !
Soit m = len(ch1), et n = len(ch2).
Dans cette approche itérative, on remplit un tableau de tableaux, de taille (m+1)*(n+1), dont les lignes correspondent aux caractères de ch1, et les colonnes à ceux de ch2.
Chaque case (i, j) contient la valeur d(i, j) ( exemple de la distance entre 'CHAT' et 'CHUTE' ) :
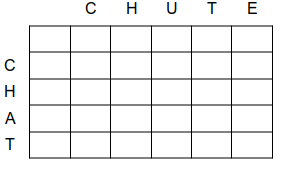
La première ligne et la première colonne correspondent chacune à une sous-chaîne vide.
Le remplissage du tableau se fait de la manière suivante :
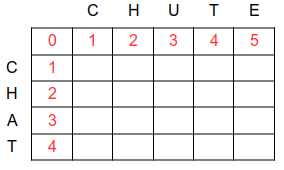

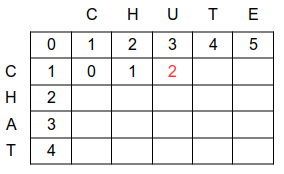
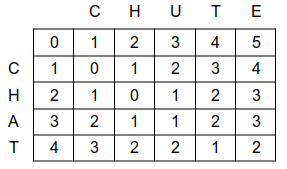
Pour chaque case (i, j), on calcule le coût minimal des insertions, suppressions et substitutions en "provenance" des cases voisines.
Implémenter, puis tester cette dernière approche.
On fera particulièrement attention à la manière d'adresser un caractère dans les chaînes ch1 et ch2...