Salut à toi, élève de NSI, comment puis-je t'aider ?
En application de toutes les structures données linéaires que vous venez de découvrir, nous vous proposons une série de problèmes mettant en œuvre l'une de ces structures (pile, file, liste, dictionnaire...).
Pour résoudre le problème qui vous sera attribué, vous devrez déterminer la structure la mieux adaptée à votre problème. Rappelez vous de la citation de Linus Torvald :
“Bad programmers worry about the code. Good programmers worry about data structures and their relationships.”
Temps prévu :
Le choix du projet n'est pas à la carte : demander au professeur celui qui vous a été attribué...
Votre travail devra se structurer de la manière suivante :
Une fois que tout cela "tourne" cela ne sera pas fini. En effet, nous allons commencer notre travail d’entraînement au grand oral. Vous devrez donc préparer :
Cette/ces page(s) sera/seront ensuite intégrée(s) sur le site pour consultation publique.
Pour la mise en forme de la page, vous pouvez récupérer cette archive, dans laquelle vous trouverez une ébauche de fichier HTML, le fichier CSS du site, et les explications pour intégrer dans votre page quelques éléments particuliers, notamment votre code pour qu'il soit formaté de la même manière que sur le site.
Vous pourrez bien entendu écrire vos propres règles de style....
Les listes de contacts personnelles peuvent atteindre des volumes de données importantes (par exemple, mon "Google contact" personnel compte aujourd'hui 1674 fiches différentes !)
Les listes de contacts de petites ou moyennes entreprises peuvent être facilement 10 ou 100 fois plus importante. Il devient essentiel d'avoir des outils de recherche efficaces.
Vous devez mettre en œuvre une liste de contacts, contenant des fiches simplifiées à deux champs :
Vous prévoirez ensuite les fonctionnalités suivantes :
La recherche des contacts devra être optimisée en O(1) (en temps constant).

Un poste de contrôle est alimenté en pièces toutes les 7 minutes. Ces pièces sont de quatre types qui nécessitent respectivement 4, 6, 8 et 9 minutes pour être contrôlés.
Les quatre types de pièces ont la même probabilité d'apparaître au poste de contrôle.
Simuler le fonctionnement du poste de contrôle pendant 1 heure, puis 80 heures.
Le programme devra afficher à chaque minute :
Un restaurant de 50 tables à 2 couverts ouvre ses portes pendant 4 heures chaque soir.
L’intervalle de temps entre l’arrivée de deux groupes de clients est d’environ 2 minutes.
Les groupes sont constitués aléatoirement de 2 à 6 convives avec des fréquences identiques.
Les tables peuvent être rassemblées pour les groupes de plus de 2 personnes. Lorsqu’un groupe arrive, il attend que des tables en nombre suffisant soient libres.
Une fois assis, le groupe reste pendant une durée aléatoirement comprise entre 60 et 120 minutes.
Simuler le fonctionnement du restaurant pendant une soirée :
Un des problèmes classique de l'informatique est la recherche de sous-chaînes dans une suite de caractères. Nous verrons cette année à ce propos L'algorithme de Boyer-Moore.
Une simplification de ce problème peut être la recherche de séries particulière.
Écrire une fonction zeros() qui prend en paramètre un tableau t et qui renvoie le plus grand nombre de zéros consécutifs dans le tableau .
Par exemple : zeros([0, 1, 1, 2, 0, 0, 0, 5, 0, 0]) renvoie 3.
Un des problèmes classique de l'informatique est la recherche de sous-chaînes dans une suite de caractères. Nous verrons cette année à ce propos L'algorithme de Boyer-Moore.
Une simplification de ce problème peut être la recherche de séries particulière.
Écrire une fonction suite_croissante() qui prend en paramètre un tableau t et qui renvoie la longueur de la plus grande suite croissante dans le tableau.
Par exemple : suite_croissante([5, 9, 7, 0, 1, 2, 3, 0, 8, 9, 10, 5, 2]) renvoie 4 ( longueur de la suite 0, 1, 2, 3 ).
En amélioration, on pourra faire en sorte que la fonction renvoie également cette suite la plus longue ( sous forme de tableau par exemple, ou de tuple ).
Comme vous le savez l'avantage de la pile par rapport à la liste est la faible complexité de ses primitives empiler et dépiler. Nous allons donc nous pencher sur la possibilité de réaliser un tri grâce à une pile.
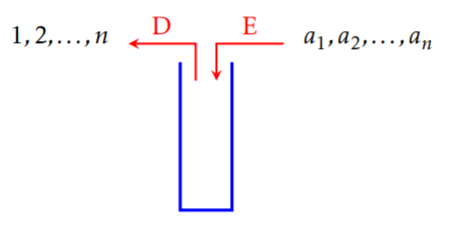
Malheureusement, toutes les listes ne sont pas triables avec une seule pile.
Si on note D et E les opérations d'empilage et de dépilage, la liste [4, 1, 3, 2] peut être triée par la séquence EEDEEDDD.
tri_en_pile() qui prend comme argument une liste et qui renvoie une liste triée si cela est possible.Un problème mathématique connu est le problème de Josèphe.
L'histoire est la suivante :
"Des soldats juifs, cernés par des soldats romains, sont obligés de former un cercle. Un premier soldat est choisi au hasard et est exécuté, le troisième à sa gauche est ensuite exécuté.
Tant qu'il y a des soldats, la sélection continue. Le but est de trouver à quel endroit doit se tenir un soldat pour être le dernier et donc être épargné.
Flavius Josèphe, peu enthousiaste à l'idée de mourir, parvint à trouver l'endroit où se tenir.
flavius(), qui prend comme paramètres :
La notation polonaise inverse (NPI) (en anglais RPN pour Reverse Polish Notation) permet d'écrire de façon non ambiguë les formules arithmétiques sans utiliser de parenthèses.
Par exemple, l’expression « 3 × (4 + 7) » peut s'écrire en NPI sous la forme : « 4 7 + 3 × ».
Bien que cette notation ait certains avantages, elle n'a été adoptée que par les calculatrices de la marque HP. On l'utilise cependant dans certains domaines comme dans les vols spatiaux, où elle présente un gain de temps non négligeable ainsi qu'un risque moindre d'erreur (pas de risque de parenthèse manquante ou décalée).
Cette page présente un émulateur de calculatrice HP-35 utilisant cette notation.
On parcourt l'expression depuis son début. On stocke les opérandes ( = les valeurs sur lesquelles on fait les calculs ) dans l'ordre où ils apparaissent.
Quand un opérateur de calcul ( +, *, - ou / ) apparaît, on récupère les deux opérandes immédiatement disponibles, et on stocke le résultat de leur calcul à leur place.
On continue le parcours de l'expression avec ce résultat intermédiaire.
Lorsque l'expression a été entièrement parcourue, le calcul est terminé et le résultat est la seule valeur stockée.
Exemple :
Calcul du résultat de l'expression : 3 10 2 - *
| Entrée | Stockage des données |
|---|---|
| 3 | 3 |
| 10 | 3 10 |
| 2 | 3 10 2 |
| - | 3 8 |
| * | 24 |
→ résultat = 24. L'expression est donc équivalente à : ( 10 - 2 ) x 3.
Écrire une fonction NPI() qui :
>>> exp = "3 10 2 - *"
>>> print(NPI(exp))
24
>>>
Indication : La méthode chaine.split(' ') permet de séparer les mots d'une chaîne selon le caractère séparateur "espace", et renvoie le tableau de ces mots.
La fonction devra de plus indiquer si l'expression était correctement écrite.
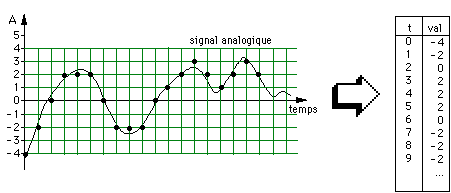
La musique digitale représente les sons comme une succession régulière dans le temps d'échantillons, c'est à dire de valeurs entières discrètes représentant l'intensité du son à des instants très rapprochées.
La durée entre deux échantillons successifs, constante, est appelée période d'échantillonnage; plus elle est petite, plus le son numérique se rapproche d'un son analogique qui est lui, continu
dans le temps; mais la quantité d'échantillons pour une même durée de son augmente alors, et donc la taille du fichier son résultant également.
Cependant, un principe fondamental du numérique est que la fréquence d'échantillonnage doit être au moins le double de la fréquence du son à numériser si l'on veut que le son soit "fidèle" à son
équivalent analogique.
Un compromis est donc à faire entre qualité sonore et taille du fichier; en pratique, des fréquences ( = inverse de la période ) d’échantillonnage de 44kHz ( = 44 ⨯ 106 échantillons par seconde ),
48 kHz voire 96 kHz sont courantes actuellement.
Le deuxième facteur qui influe sur la qualité d'un son numérique est la quantification, qui donne le nombre de valeurs entières possibles pour coder un échantillon : plus ce nombre est grand, plus la numérisation sera "précise". Actuellement, des quantifications sur 16 voire 24 bits sont courantes.
De très nombreuses façons de synthétiser des sons ont été envisagées, dans un premier temps pour reproduire des instruments réels, puis avec l'avènement des synthétiseurs, pour créer des sonorités qui n'existaient pas auparavant.
Avec la synthèse numérique du son par ordinateur, il est maintenant possible de créer directement les échantillons en leur donnant la valeur que l'on veut, afin de reproduire n'importe quel sonorité.
Bien que très simple sur le papier et à programmer, il permet de synthétiser des sons qui se rapprochent d'instruments à cordes pincées ( guitare, harpe, ...) ou de percussions extrêmement réalistes.
Cet algorithme se présente ainsi :
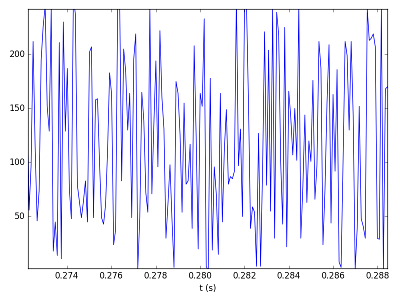
Le bruit blanc à l'origine du son...
Et c'est tout !! Assez incroyablement, le son produit est vraiment comparable à celui d'une corde de guitare ( pour obtenir un son de percussion, c'est un peu plus compliqué ).
Cet algorithme permet de créer un son en "temps réel" mais vous vous en servirez pour construire des fichiers au format .WAV destinés à être lus ensuite.
Pour cela, vous aurez à votre disposition ce module qui permet d'enregistrer un fichier son en fournissant le tableau des échantillons. Bien lire la docstring des fonctions
de ce module pour comprendre leur fonctionnement.
Vous allez écrire un script Python qui utilise l’algorithme K-S pour créer le tableau des échantillons qui permettra ensuite d'écrire des fichiers .WAV de sons de guitare de fréquence donnée; voici quelques indications :
Pour des raisons sur lesquelles nous ne nous étendrons pas, la fréquence d'échantillonnage doit être assez élevée pour obtenir des résultats corrects, et ce d'autant plus que la fréquence du son à créer est élevée ( sons aigus ); vous prendrez donc : fech = 20000 Hz.
La durée de l'ensemble des échantillons du buffer doit correspondre à la période T du son à créer.
On appelle f la fréquence du son à créer, et fech la fréquence d'échantillonnage; on montre que le nombre N d'échantillons du buffer est donnée par la relation :
N = fech / f.
Pour obtenir des résultats corrects, vous créerez des sons de fréquence f ≈ 200 - 1000 Hz
Le principe d'application de l'algorithme K-S est le suivant :

On se rend vite compte que le son s'amortit d'autant plus vite que sa fréquence est élevée, ce qui est d'ailleurs cohérent avec une vraie guitare.
Cependant, on peut améliorer la sonorité des sons aigus de la manière suivante : au lieu de calculer la moyenne de deux échantillons successifs, on en calcule la moyenne pondérée par un coefficient ( noté α ), compris entre 0 et 1 :
Ceci marche mieux avec des sons de haute fréquence ( avec des sons graves, le son sonne alors trop "métallique"...).
Faites varier α entre 0,5 et 0,9.
on rappelle que la moyenne pondérée de deux valeurs A et B, de poids respectifs α et β, est donnée par : m = ( 1 α + β ).(α.a + β.b)
L'algorithme reste sensiblement le même, mais la façon de créer les données change : un nouvel échantillon n'est plus toujours égal à la moyenne de deux échantillons successifs; il ne lui est égal qu'avec une probabilité de 50%, et sinon il est égal à l'opposé de cette moyenne. Autrement dit, l'échantillon a une chance sur deux d'être égal à la moyenne, et une chance sur deux d'être égal à son opposé...
Vous allez donc modifier le script précédent pour appliquer ce principe.
Il va falloir se servir du générateur de nombres pseudo-aléatoires de Python pour simuler des probabilités.
Le principe est le suivant : on tire un nombre au hasard entre 0 et 100; si ce nombre est inférieur à 50, alors la probabilité est vérifiée, et sinon elle n'est pas vérifiée ( ce qui correspond bien à 50%, soit
une chance sur deux...)
Attention, dans le cas de percussions, la taille du buffer ( qui dépend de la "fréquence" f du son ) ne conditionne plus la hauteur du son mais la durée de l'extinction du son : plus le buffer est petit ( donc f est grande ), et plus le son est "étouffé" rapidement.
C'est alors la valeur de f qui permet de reproduire différentes percussions, il ne faudra pas hésiter à expérimenter !