Recherche textuelle

Faites un CTRL+F dans n'importe quel logiciel ( traitement de texte, navigateur web,...) : en une fraction de seconde, l'ordinateur détecte si dans le texte du document ouvert se trouve une chaîne de caractères ou un motif particulier que vous recherchez.

On peut se poser la question de l'algorithme qui permet cette recherche si rapide, même dans le cas de gros documents...de plus, cette recherche de motif trouve son application dans d'autres domaines, comme l'analyse de l'ADN afin d'y détecter la présence d'un gène particulier.

Algorithme naïf

Principe

On fait "glisser" progressivement le motif depuis le début du texte, en le décalant à chaque fois d'un caractère vers la droite.

A chaque "décalage", on compare le premier caractère du motif avec le caractère correspondant dans le texte :

si les deux caractères ne correspondent pas, on passe au décalage suivant
si les caractères correspondent, on compare le deuxième caractère du motif, puis si il y a correspondance, le troisième, etc...
Si tous les caractères du motif correspondent à ceux du texte, alors on a trouvé le motif dans le texte, sinon on passe au décalage suivant dans le texte.

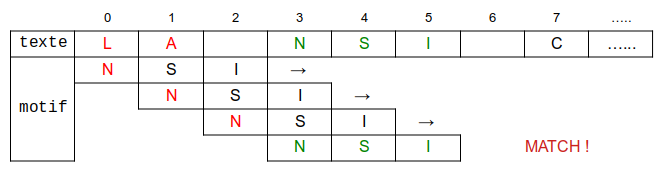
Texte :

Motif :

Nombre de comparaisons :

Algorithme


fonction recherche_naive: texte, motif
	ENTRÉES :
		texte = texte de n caractères
		motif = motif de p caractères ( p < n )
	SORTIE :
		le tableau des occurrences du motif dans le texte, c'est à dire le tableau du (ou des) indice(s) dans le texte où a été trouvé le motif
		Tableau vide si le motif n'a pas été trouvé
	
	occurrences ← tableau vide
	
	pour i variant de 0 à la fin du texte moins la longueur du motif :
		j ← 0 
		tant que l'on n'a pas atteint la fin du motif, et que le caractère dans le motif correspond au caractère de même position dans le texte : 				
			j ← j + 1
		
		si on a parcouru tout le motif   // alors on l'a trouvé dans le texte !
			occurrences ← i
			
	renvoyer occurrences

à la ligne 12 débute la boucle qui va parcourir le texte en se décalant d'un caractère vers la droite à chaque "tour". La variable i indique la position dans le texte à partir de laquelle on va chercher la présence du motif.
Exprimer la borne supérieure de cette boucle en fonction de n et p.
à la ligne 14 commence la boucle qui va vérifier si le motif se trouve dans le texte pour chaque position i.
On utilise pour cela une variable j qui va pointer sur le premier caractère du motif, puis, si ce caractère correspond à celui de même position dans le texte, va pointer sur le suivant, puis le troisième, etc...tant que les caractères correspondent : si à l'issue de cette boucle on a parcouru le motif en entier, c'est donc qu'il est présent dans le texte à la position i , que l'on stocke alors dans le tableau des occurrences ( lignes 16 et 17 ).
Exprimer la double condition à vérifier à chaque tour de cette deuxième boucle.
Comment traduire à la ligne 17 : "si on a parcouru tout le motif" pour savoir si le motif était présent dans le texte à l'indice i ?

SOLUTION

Complexité

On appelle n = le nombre de caractères du texte, et p = le nombre de caractères du motif.

Le pire des cas est lorsque le texte est composé du même caractère ( par exemple 'aaaaaaaa' ) et que le motif est lui aussi composé de ce caractère, sauf son dernier ( par exemple 'aaaab' ).

Dans ce cas, on doit parcourir l'intégralité du texte moins la longueur du motif, soit n - p décalages; et à chaque décalage, on doit faire p comparaisons avant de se rendre compte que le motif ne correspond pas et donc passer au décalage suivant.

On fait donc dans ce cas en tout (n - p) ⨯ p comparaisons : comme généralement p << n, la complexité en temps est donc en O(n ⨯ p), peu efficace surtout si le motif est long !

On doit pouvoir faire mieux...

Algorithme de Boyer-Moore-Horspool

Principe

L'algorithme de Boyer-Moore-Horspool ( simplification de l'algorithme de Boyer-Moore, voir ci-dessous ), effectue la vérification à l'envers, c'est à dire en partant non pas du début mais de la fin du motif.

Prenons un exemple :

Si l’algorithme cherche "RECURSION" dans un texte, il teste d’abord non pas le premier, mais le dernier caractère du motif ( ici, le 9^ème caractère du texte ); plusieurs situations peuvent alors se présenter :

si on trouve un N ( = dernier caractère du motif ) : on regarde si le 8^ème caractère est un O, puis le 7^ème un I,... jusqu’au 1^er.
Si tous les caractères correspondent, on a trouvé le motif.
Si les autres caractères ne correspondent pas, on en déduit que le motif ne peut commencer au mieux qu'en 10^ème position du texte : l'algorithme décale le motif d'une longueur complète, et "saute" alors directement à la 18^ème position pour rechercher un N.

Le N correspond, mais pas les caractères précédents : le motif ne peut donc se trouver que 9 positions ( = la longueur du motif ) plus à droite.
si on trouve en 9^ème position une lettre n’apparaissant pas dans le motif : cette situation est similaire à la précédente, où l'on peut donc aussi décaler le motif d'une longueur complète : ainsi, on ne vérifie qu'un seul caractère au lieu de dix.
si on trouve par exemple un I au lieu d’un N en 9^ème position : il se peut que ce soit le I de RECURSION, auquel cas le N serait 2 positions plus à droite : l’algorithme décale alors le motif de 2 positions pour faire "coïncider" le I du motif et celui du texte, et recherche alors le N (puis éventuellement le O, le I...).

Le N ne correspond pas, mais on trouve un I qui fait partie du motif : on le décale donc de 2 caractères.

Dans cet algorithme, le décalage appliqué au motif n'est donc pas de 1 position, mais dépend du caractère lu : dans le cas de RECURSION, +9 si le caractère est un N ou n’est pas dans le motif, +7 pour un E, +2 pour un I, etc...
Si une même lettre apparaît plusieurs fois dans le motif, on retiendra logiquement le plus petit décalage ( donc celui correspond au caractère le plus à droite du motif ).

L'algorithme décale donc beaucoup plus "vite" le motif vers la droite, et ce d'autant plus que le motif est long : on arrive donc plus rapidement à la fin du texte, la complexité en temps est bien meilleure que celle de la recherche naïve.

Texte :

Motif :

Nombre de comparaisons :

Algorithme

Plutôt que de faire le calcul à chaque fois, on préfère pré-traiter le motif afin de calculer une seule fois le décalage correspondant à chaque caractère de ce motif.

Pour cela, on peut par exemple utiliser un tableau associatif ( = dictionnaire en Python ) dont les clés seront les caractères du motif et les valeurs celles du décalage correspondant.

Le dernier caractère du motif ne peut pas être inclus dans ce dictionnaire, car son décalage serait de 0 si on le calculait comme pour les autres caractères du motif : en rencontrant ce caractère, l'algorithme entrerait alors dans une boucle infinie sans parcourir la suite du texte !

On traitera donc son cas à part de celui des autres caractères du motif.

Si on suppose disposer d'une fonction créant le dictionnaire des décalages, l'algorithme de Boyer-Moore-Horspool est alors le suivant :


fonction recherche_BMH: texte, motif
	ENTRÉES :
		texte = texte de n caractères
		motif = motif de p caractères ( p < n )
	SORTIE :
		le tableau des occurrences du motif dans le texte, c'est à dire le tableau du (ou des) indice(s) dans le texte où a été trouvé le motif
		Tableau vide si le motif n'a pas été trouvé
	
	occurrences ← tableau vide
	dec ← decalages(motif)    // appel à la fonction de construction du dictionnaire des décalages
	
	i ← 0
	tant que i <= n - p :
		j ← p - 1    	// indice du dernier caractère du motif
		tant que j >= 0 et que texte[i + j] = motif[j] : 				
			j ← j - 1
		
		si j = - 1 :		// on a parcouru tout le motif, alors on l'a trouvé dans le texte !
			occurrences ← i
			i ← i + longueur du motif
		sinon si texte[i+j] = motif[p-1]		// 1^er cas : caractère = dernier caractère du motif
			i ← i + longueur du motif
		sinon si texte[i+j] n'est pas dans motif : // 2ème cas : caractère pas dans le motif 
			i ← i + longueur du motif
		sinon :
			i ← i + décalage correspondant au caractère texte[i+j]  // 3ème cas : caractère dans le motif, décalage à appliquer
	
	renvoyer occurrences

Comme les décalages ne sont pas prévisibles à l'avance, on ne peut utiliser une boucle for...range pour parcourir le texte, c'est pourquoi on trouve ici une boucle while à la place.

Conclusion sur la complexité

La complexité de la phase de pré-traitement est en O(p + taille de l'alphabet utilisé), mais ce pré-traitement n'est fait qu'une seule fois.

La démonstration de la complexité en temps de la recherche proprement dite est difficile, et de toute façon pas au programme...

Cette complexité est généralement sous-linéaire, c'est à dire inférieure à O(n) puisqu'on "saute" ainsi de grands pans de texte (l'algorithme n'a pas "besoin" de lire le texte dans son intégralité...); on peut raisonnablement estimer la complexité moyenne à O(n/p).

L'algorithme de Boyer-Moore

L'algorithme de Boyer-Moore, dont dérive celui-ci, utilise deux tables de décalages :

La première se base sur le caractère du texte qui a été comparé au dernier caractère du motif; c'est donc la même table que dans l'algorithme Boyer-Moore-Horspool.
La deuxième se base sur la comparaison de suffixes, c'est à dire de combinaisons de plusieurs caractères du motif sauf le premier caractère.
Par exemple, les suffixes dans CHIEN sont N, EN, IEN et HIEN.
Cette table indique le décalage à effectuer lorsque l'on rencontre un suffixe donné dans le texte; elle est beaucoup plus délicate à calculer que la première...

En pratique, l’algorithme de Boyer-Moore utilise les deux tables de sauts. À chaque étape, il détermine les décalages fournis par les deux tables et prend le meilleur.

Pour plus de précisions, la page de Wikipedia.

Implémentation Python

Algorithme naïf

Écrire une fonction rech_naive() qui implémente la recherche naïve d'un motif dans un texte.

Réalisez les tests proposés.

def rech_naive(texte: str, motif: str)->list: """ Fonction de recherche naïve d'un motif dans un texte. Entrées : texte = le texte dans lequel rechercher motif = le motif à rechercher Sortie : le tableau des indices des occurrences du motif dans le texte un tableau vide si le motif ne se trouve pas du tout dans le texte. """ pass print(rech_naive("un chasseur sachant chasser doit savoir chasser sans son chien","chien")) # [57] print(rech_naive("un chasseur sachant chasser doit savoir chasser sans son chien","doit")) # [28] print(rech_naive("un chasseur sachant chasser doit savoir chasser sans son chien","chiot"))# [] print(rech_naive("un chasseur sachant chasser doit savoir chasser sans son chien","ass")) # [5, 22, 42]

SOLUTION

Algorithme Boyer-Moore-Horspool

Calcul des décalages

La première chose à faire est d'écrire une fonction qui créera le dictionnaire des décalages pour chaque caractère du motif.

en complétant le tableau de l'exemple ci-contre, déterminer la relation qui permet de calculer le nombre de positions dont il faudra déplacer le motif pour chacun de ses caractères.
écrire alors une fonction decalages() qui crée et renvoie le dictionnaire des décalages pour le texte passé en paramètre.
Réalisez les tests proposés pour vérifier son bon fonctionnement.
def decalages(motif: str)->dict: """ Fonction qui calcule le décalage pour chaque caractère d'un motif. Entrée : motif = le motif à pré-traiter Sortie : le dictionnaire associant à chaque caractère ( clé ) son décalage ( valeur ) """ pass print(decalages("chien")) # {'c': 4, 'h': 3, 'i': 2, 'e': 1} print(decalages("doit")) # {'d': 3, 'o': 2, 'i': 1} print(decalages("ass")) # {'a': 2, 's': 1}

SOLUTION

Recherche Boyer-Moore-Horspool

Écrire une fonction rech_BMH() qui implémente la recherche d'un motif dans un texte selon l'algorithme.

Cette fonction fera appel à la fonction decalages pour récupérer le dictionnaire des décalages.

Réalisez les tests proposés pour vérifier la correction de votre fonction.

def decalages(motif: str)->dict: # Code précédent pass def rech_BMH(texte: str, motif: str)->list: """ Fonction de recherche d'un motif dans un texte selon l'algorithme de Boyer-Moore-Horspool. Entrées : texte = le texte dans lequel rechercher motif = le motif à rechercher Sortie : le tableau des occurrences du motif un tableau vide si le motif n'est pas présent dans le texte """ pass print(rech_BMH("un chasseur sachant chasser doit savoir chasser sans son chien","chien")) #[57] print(rech_BMH("un chasseur sachant chasser doit savoir chasser sans son chien","doit")) # [28] print(rech_BMH("un chasseur sachant chasser doit savoir chasser sans son chien","chiot")) # [] print(rech_BMH("un chasseur sachant chasser doit savoir chasser sans son chien","ass")) # [5, 22, 42]

SOLUTION

Comparaison de l'efficacité des deux algorithmes

Pour de petits textes, il n'y pas beaucoup de différences dans le temps d'exécution des deux algorithmes...

Il serait plus intéressant de tester cette différence dans le cas d'un gros volume de texte, comme par exemple rechercher les 451 occurrences du mot 'Valjean' dans le tome 5 des Misérables de Victor Hugo.

Vous trouverez ici le texte ( en anglais ) des Misérables de V. Hugo au format .txt

Après avoir ouvert ce fichier et extrait son texte, utiliser le module timeit pour mesure le temps exécution de 5 recherches successives du mot 'Valjean' dans le texte, à l'aide de chacun des deux algorithmes.

Faire le même travail avec cette fois, un paragraphe entier comme motif à rechercher : que peut-on remarquer ?

Attention à ne pas prendre en compte dans la comparaison des temps d'exécution, celui nécessaire à la fonction decalages : ce traitement ne doit être fait qu'une seule fois pour une même recherche !

Il est donc ici préférable de "déporter" l'appel à la fonction decalages dans le programme principal, et à ensuite passer le dictionnaire des décalages comme argument à la fonction de recherche BMH.

from timeit import timeit # attention, l'utilisation de timeit peut être longue en ligne ! def rech_naive(texte: str, motif: str)->list: # Code précédent pass def decalages(motif: str)->dict: # Code précédent pass def rech_BMH(texte: str, motif: str, dec: dict)->list: # Code précédent modifié : on passe le dictionnaire des décalages comme paramètre à cette fonction pass

SOLUTION