Exercices Récursivité

Dans tous ces exercices, bien penser aux 3 règles à suivre pour écrire un algorithme récursif :

identifier le cas général
déterminer le cas de base
vérifier que le cas général tend forcément vers le cas de base ( = l'algorithme termine )

Le compte à rebours

Version descendante

Écrire une fonction récursive qui :

prend en paramètre un entier n
affiche un compte à rebours de n jusqu'à 1, puis affiche "Ignition !


print(compte_rebours(10))

10
9
8
7
6
5
4
3
2
1
Ignition !
>>>

def compte_rebours(n: int)->None: pass

SOLUTION

Version ascendante ( plus difficile )

Écrire une fonction récursive qui affiche un compte à rebours de 1 jusqu'à n, puis affiche "Ignition !


print(compte_rebours(10))

1
2
3
4
5
6
7
8
9
10
Ignition !
>>>

Indication : la fonction aura 2 paramètres, l'un ( fixe ) qui indique la valeur limite à atteindre ( ici 10 ), et un autre ( variable ).

def compte_rebours(n: int, i = 0)->None: pass

SOLUTION

La fonction factorielle

En mathématiques, la fonction factorielle d'un entier n ( notée n! ) est définie par : n! = 1 * 2 * 3 * 4 x ..... * n

écrire une fonction itérative qui calcule la factorielle d'un entier n passé en paramètre.
écrire la fonction récursive qui réalise le même travail; pour cela :
- déterminer la relation de récurrence qui existe entre le niveau n et le niveau n-1 de la récursion ( autrement dit : trouver le lien qu'il y a entre n! et (n-1)! ).
- déterminer le cas de base et le résultat qui doit alors être renvoyé
vérifiez bien entendu que vos deux algorithmes donnent le même résultat pour un même entier n !

def factorielle_iter(n: int)->int: pass def factorielle_recurs(n: int)->int: pass

SOLUTION

Construction d'un tableau

Écrire une fonction récursive qui renvoie un tableau dont les éléments sont les entiers compris entre deux entiers a et b.

def construction_tableau(a: int, b: int)->list: pass

SOLUTION

Élément dans un tableau

Écrire une fonction récursive qui détermine si un élément de valeur donnée est présent ( True ) ou non ( False ) dans un tableau.

def est_dans(valeur: int, tab: list)->bool: pass

SOLUTION

Parité d'un nombre

Vous connaissez ( normalement... ) l'existence de l'opérateur modulo ( en Python % ) qui donne le reste d'une division; pour savoir si un entier est pair, il suffit alors de déterminer si le reste de sa division par 2 est égal à 0 ( pair ) ou pas ( impair ). Par exemple : 42 % 2 == 0 donc 42 est pair, et 15 % 2 != 0 donc 15 est impair.

On peut cependant utiliser un principe récursif pour tester la parité d'un entier n :

si n = 0, on renvoie True
et si n est strictement positif, on renvoie l'opposé de la parité de n-1.

Par exemple, pour trouver la parité de 3, on calcule récursivement celle de 2, puis celle de 1, et enfin celle de 0. Mathématiquement, comme 0 est pair, son suivant 1 est impair, et donc 2 est pair, et par conséquence 3 est impair.
Du point de vue de l'algorithme, si on appelle est_pair() la fonction récursive, alors est_pair(0) est True, donc est_pair(1) est not True, c'est-à-dire False, et ainsi de suite...

Écrire une fonction récursive qui renvoie True si l'entier passé en paramètre est pair, False sinon.

def est_pair(n: int)->bool: pass

SOLUTION

Somme des éléments d'un tableau

Écrire une fonction récursive qui :

prend en paramètre un tableau L
retourne la somme S des éléments du tableau L


L = [12, 45, 2, 23, 7, 8 ,1]
print(somme_recurs(L))

98
>>>

def somme_recurs(tab: list)->int: pass

SOLUTION

Somme des chiffres d'un nombre

Écrire une fonction récursive qui prend un nombre n comme paramètre, et qui renvoie la somme de ses chiffres :


print(somme_chiffres(4561))

>>> 16

Indication :

le chiffre le plus à droite d'un nombre est égal au reste de la division de ce nombre par 10.
les autres chiffres du nombre forment un nombre lui-même égal au quotient du nombre par 10.

Par exemple, si N = 4561 :

4561 % 10 = 1
4561 // 10 = 456

def somme_chiffres(N: int)->int: pass

SOLUTION

Miroir d’une chaîne de caractère

Écrire une fonction miroir(chaine) récursive qui :

prend comme paramètre une chaîne de caractères
renvoie le « miroir » de la chaîne; par exemple, le miroir de "abcde" est "edcba".

def miroir(chaine: str)->str: pass

SOLUTION

Tableau trié ?

Écrire une fonction récursive qui :

prend en paramètre un tableau T
retourne True si le tableau L est trié, ou False sinon

On peut remarquer qu'un tableau est trié si, pour chacun de ses éléments on vérifie : T[n-1] < T[n] ( ou T[n-1] <= T[n] si il y a des doublons ).

Vous pourrez tester votre fonction avec les deux tableaux ci-dessous :


	# un tableau non trié
	T1 = [312, 472, 772, 389, 128, 189, 941, 163, 300, 151, 535, 321, 440, 400, 715, 209, 185, 775, 840, 911, 320, 299, 590, 593, 243, 634, 592, 220, 259, 287, 235, 495, 982, 49, 991, 481, 898, 34, 982, 103, 874, 436, 84, 736, 538, 22, 81, 274, 996, 44, 733, 518, 321, 992, 281, 539, 978, 681, 622, 941, 234, 273, 849, 612, 173, 113, 427, 434, 958, 516, 722, 387, 599, 520, 699, 539, 284, 972, 988, 246, 946, 716, 950, 341, 237, 488, 523, 583, 57, 308, 548, 323, 297, 846, 151, 531, 203, 532, 115, 346]
	
	# un tableau trié		
	T2 = [8, 29, 34, 52, 61, 79, 93, 105, 119, 122, 137, 167, 175, 193, 194, 198, 203, 215, 217, 224, 243, 254, 257, 257, 258, 282, 295, 303, 317, 323, 325, 332, 338, 349, 354, 358, 379, 380, 386, 404, 417, 418, 434, 446, 447, 448, 452, 456, 458, 465, 478, 481, 482, 484, 514, 515, 516, 552, 554, 559, 568, 571, 575, 587, 603, 628, 641, 663, 669, 692, 693, 696, 703, 709, 713, 714, 715, 729, 730, 744, 751, 752, 765, 774, 775, 805, 807, 812, 816, 828, 883, 890, 915, 920, 925, 931, 939, 946, 950]

def est_trie(T: list)->bool: pass

SOLUTION

Conversion décimal → binaire

Ah, un grand classique...Le but est de transformer un entier en base 10 en une chaîne de caractères '0' et '1' représentant le nombre en base 2.

Il existe deux façons de réaliser cette conversion, qui se prêtent toutes les deux très bien à la récursivité...

Une vidéo qui présente ces deux méthodes.

Méthode par soustraction

Rappelez-vous comment "fonctionne" la numération binaire : chaque bit correspond, de la droite vers la gauche du nombre, à une puissance croissante de 2 : 2⁰, 2¹, 2², etc...

Par exemple : 101101₂ = 1 x 2⁰ + 0 x 2¹ + 1 x 2² + 1 x 2³ + 0 x 2⁴ + 1 x 2⁵ = 45₁₀

L'idée de la méthode par soustraction est la suivante :

on compare le nombre à convertir à la puissance de 2 la plus grande selon le nombre de bits utilisés pour exprimer le nombre ( un octet par exemple )

si le nombre est plus grand ou égal : cette puissance de 2 est "incluse" dans le nombre et le bit correspondant est donc '1'. On soustrait alors cette puissance au nombre à convertir.
si le nombre est plus petit : cette puissance de 2 n'est donc "pas incluse" dans le nombre et le bit correspondant est donc '0'. On ne change pas le nombre à convertir.

on recommence à l'étape 1 ( soit avec le reste de la soustraction, soit avec le nombre inchangé ) en considérant la puissance de 2 immédiatement inférieure
on s'arrête une fois qu'on a traité la puissance 2⁰.

Le nombre binaire est alors la suite des bits dans l'ordre où ils sont apparus lors de l’exécution de l’algorithme.

Appliqué à la conversion de 45₁₀, cela donne ( sur 6 bits ) :

n = 5 : 45 > 2⁵ ( = 32 ) → '1', et on continue avec 45 - 32 = 13
n = 4 : 13 < 2⁴ ( = 16 ) → '0', et on continue avec 13
n = 3 : 13 > 2³ ( = 8 ) → '1', et on continue avec 13 - 8 = 5
n = 2 : 5 > 2² ( = 4 ) → '1', et on continue avec 5 - 4 = 1
n = 1 : 1 < 2¹ ( = 2 ) = → '0', et on continue avec 1
n = 0 : 1 = 2⁰ ( = 1 ) → '1' : terminé

Écrire une fonction récursive qui :

prend comme paramètre un entier D et un nombre de bits n
renvoie comme résultat une chaîne de caractères représentant le nombre D exprimé en base 2 sur n bits, converti avec la méthode par soustraction.

On fera attention ( ou alors le programme devra gérer ce problème potentiel ) à ce que le nombre de bits n soit suffisant pour exprimer D en base 2.

def dec2bin_soustraction(D: int, n: int)->str: pass

SOLUTION

Méthode par division

Cette méthode est moins intuitive. En voila la version itérative :


def dec2bin_division(D):
	"""
		Entrée : un entier D
		Sortie : une chaîne de caractères représentant D en base 2
	"""

	b = "" # chaîne qui contiendra le résultat
	q = D

	while q != 0:
		r = q % 2 # calcul du reste de la division du nombre par 2
		b = str(r) + b # ajout du bit en début de chaîne
		q = q // 2 # calcul du quotient entier du nombre par 2

	return b

On peut remarquer que, dans cette version, il n'est pas nécessaire de préciser le nombre de bits : celui-ci est déterminé "automatiquement" par l'algorithme, qui est, d'autre part, un peu plus efficace que le précédent.

Écrire une fonction récursive qui :

prend comme paramètre un entier D
renvoie comme résultat une chaîne de caractères représentant le nombre D exprimé en base 2 avec la méthode par division.

Bien identifier, entre les deux calculs faits par l'algorithme ( le quotient entier et le reste de la division par 2 ) celui dont le résultat doit être passé en argument au niveau inférieur de la récursion.

def dec2bin_division(D: int)->str: pass

SOLUTION

Nombre en chiffres romains

Principe

Les Romains utilisaient une numération additionnelle, donc pas de position comme le sont la base 2 ou notre base décimale ( leurs nombres n'étaient pas exprimé dans une certaine base ); c'est ce qui fait la difficulté pour nous à rapidement "décoder" un nombre écrit en chiffres romains.

Les chiffres romains avec leur équivalent en base 10 sont les suivants :

M = 1000
D = 500
C = 100
L = 50
X = 10
V = 5
I = 1

Conversion en base 10

Il faut faire la somme des valeurs de tous les chiffres du nombre, en suivant les règles suivantes :

si un chiffre n'est pas suivi d'un chiffre de plus grande valeur, alors on additionne simplement la correspondance (M=1000, L = 50, ...) à la somme de tout le reste
si un chiffre est suivi d'un autre de plus grande valeur, alors on le soustrait de la somme de tout le reste.

Pour calculer "la somme de tout le reste", il faut appliquer à nouveau ce principe sur le reste, d'où l'utilisation de la récursivité !

XIV = 10 - 1 + 5 = 14
MMXX = 1000 + 1000 + 10 + 10 = 2020
MCMLXVII = 1000 - 100 + 1000 + 50 + 10 + 5 + 1 + 1 = 1967

Écrire une fonction récursive rom2dec(rom) qui :

prend en paramètre une chaîne rom représentant un nombre en chiffres romains
retourne un entier, conversion de rom en base 10


>>> print(rom2dec("MMXX"))

2020
>>>

Pour l'équivalence entre chiffres romains et valeurs décimales, on pourra utiliser avec profit un dictionnaire.

def rom2dec(rom: str)->int: pass

SOLUTION

Algorithmes de tri

Vous vous souvenez ( bien sûr ) des algorithmes de tri de tableau ?

Ils font partie de la liste des algorithmes à connaître.

Tri par sélection

Ce tri est parfois appelé "naïf" au sens de "le plus simple qui vienne à l'esprit, sans souci d'efficacité ou d'optimisation".

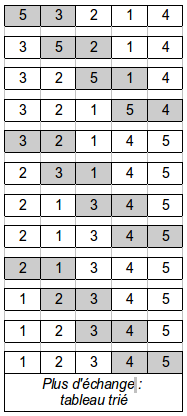
Le principe consiste à rechercher le minimum du tableau et de le placer en début de tableau, puis recommencer sur le sous-tableau des autres éléments.
Par exemple, prenons le tableau L = [6,9,1,5,3,3,10,4,8,2]. A l'étape 1, on recherche la valeur minimum du tableau (ici c'est 1 en position 3), puis on échange cette valeur avec la première valeur du tableau (ici, c'est 6). Le tableau L devient alors L = [1,9,6,5,3,3,10,4,8,2].
On recommence alors ce processus pour le sous-tableau [9,6,5,3,3,10,4,8,2]. Le minimum est 2, et on l'échange avec 9. Le tableau L devient alors [1,2,6,5,3,3,10,4,8,9].
On recommence ainsi jusqu'à ce que le sous-tableau à trier soit de taille 1, ce qui signifie que l'on est arrivé en bout de tableau.

Écrire la version itérative d'une fonction de tri par sélection pour vous remettre le principe en tête. Vous pouvez la tester avec le tableau non trié de l'exercice 8.
écrire ensuite la version récursive de cette fonction.

def tri_selection_iter(tab: list)->list: pass def tri_selection_recurs(tab: list)->list: pass

SOLUTION

Tri par insertion

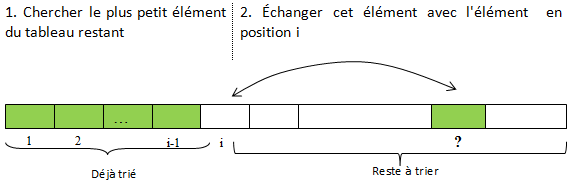
C'est la méthode que l'on utilise intuitivement pour trier par exemple un jeu de cartes.

Le principe consiste à insérer successivement chaque élément L[i] à sa bonne place dans la partie du tableau déjà trié L[0:i].
Par exemple, prenons le tableau L = [9,6,1,5,3,3,10,4,8,2]. À l'étape 1, on insère la valeur 6 à sa place dans le tableau trié [9]. Le tableau L devient alors L = [6,9,1,5,3,3,10,4,8,2].
On recommence alors ce processus en insérant la valeur 1 dans le sous-tableau [6,9]. On obtient alors L = [1,6,9,5,3,3,10,4,8,2].
On recommence ainsi jusqu'au traitement du dernier élément du tableau.

Écrire la version itérative d'une fonction de tri par insertion pour vous remettre le principe en tête. Vous pouvez la tester avec le tableau non trié de l'exercice 8.
écrire ensuite la version récursive de cette fonction.

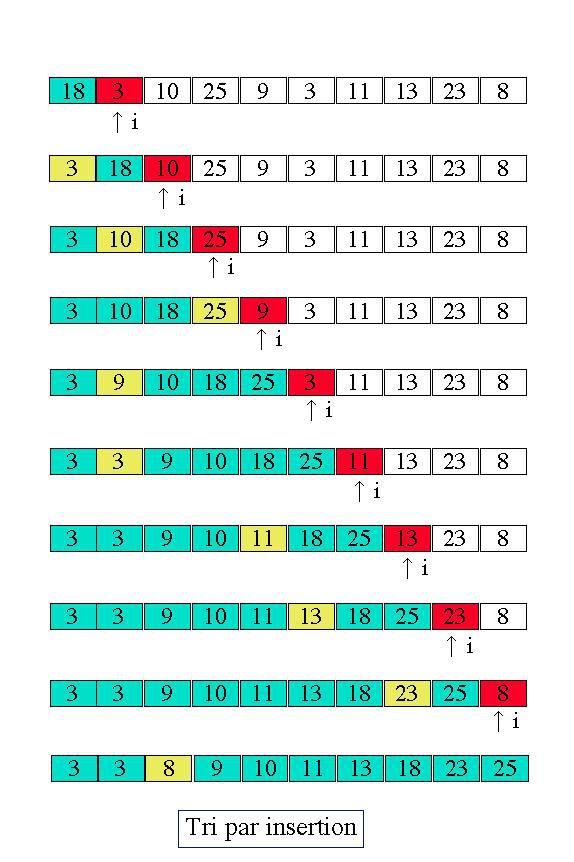
Indication : pour placer un élément à sa bonne place, on peut le faire "remonter" depuis le début du tableau, en échangeant sa place avec un élément en place tant que l'élément à placer est plus grand que l'élément en place.

def tri_insertion_iter(tab: list)->list: pass def tri_insertion_recurs(tab: list)->list: pass

SOLUTION

Tri à bulles

Un p'it dernier pour la route, mais celui-ci ne fait pas partie des algorithmes à connaître.

Le principe consiste à faire des parcours successifs du tableau en échangeant les valeurs contiguës mal classées.
Le premier parcours du tableau place le maximum de la liste en dernière position. On recommence ensuite le processus sur le sous-tableau obtenue en ne considérant pas ce maximum, puisqu'il se trouve à la "bonne" place.
Le tableau est trié lorsqu'il n'y a plus aucun élément à traiter.

Le nom de l'algorithme vient du fait qu'il fait "remonter" les plus grands éléments vers la fin du tableau comme des bulles dans un liquide.

On voit tout de suite qu'il n'est pas très efficace puisqu'il demande un très grand nombre de parcours du tableau avant que tous les éléments aient été correctement échangés.

Écrire la version itérative d'une fonction de tri à bulles. Vous pouvez la tester avec le tableau non trié de l'exercice 8.
écrire ensuite la version récursive de cette fonction.

def tri_bulles_iter(tab: list)->list: pass def tri_bulles_recurs(tab: list)->list: pass

SOLUTION