Récursivité

On parle de récursivité d'un algorithme lorsqu'il utilise une fonction qui vérifie la particularité suivante :

Cet appel peut se faire une fois, deux fois, ou plusieurs fois de suite : la fonction se retrouve "imbriquée dans elle-même" !

Étrange particularité...pour mieux illustrer ce concept "d'appel à soi-même", voila quelques exemples de récursivité en dehors du domaine de l'informatique :

Dans tous ces exemples, on se sert d'un objet pour fabriquer l'objet lui-même ! C'est ça le principe de la récursivité...mais en informatique, au lieu d'une "mise en abyme" infinie comme dans ces exemples, il faut impérativement que ce "bouclage sur soi-même" s'arrête à un moment ou un autre !

La récursivité s'oppose à la programmation itérative, où les instructions s’exécutent les unes après les autres jusqu'à arriver au résultat recherché; nous verrons quand il est possible de transformer un programme itératif en programme récursif ( l'inverse étant généralement beaucoup plus difficile ), et dans quel cas lequel de ces paradigmes est le "meilleur" à utiliser.

Exemples d'introduction

Un premier exemple un peu inutile...

Considérons le code suivant :

Ah oui, super...moi je peux faire ça avec une simple boucle...

Et effectivement, une boucle peut facilement être transformée en un algorithme récursif ( et vice et versa ), mais ce qui nous intéresse ici, c'est : comment ça marche ???

Examinons pour cela le déroulement du script :

1. on commence par un appel à la fonction f(n) en lui passant l'argument 5
2. dans la fonction, on trouve une condition, qui n'est pas alors vérifiée
3. ...donc le else est exécuté : on affiche donc "Salut !"
4. et puis....on rappelle la fonction f(n) à partir d'elle-même !
   Sauf que cette fois, on lui passe comme argument 5 - 1 = 4; le processus recommence donc à l'étape 2, puis de même avec les arguments 3, puis 2, puis 1
5. vient alors un moment ou l'argument passé est égal à 0; la condition est alors vérifiée : on affiche Bye-Bye !, et....tout s'arrête : la fonction f(n) n'est plus rappelée.

Et bien voila, le résultat de la fonction f(n) a été obtenu en faisant des appels successifs à elle-même, et c'est ça la base de la récursivité.

Cet exemple n'est pas très intéressant par rapport à une simple boucle, car chaque récursion ( = appels successifs de la fonction à elle-même ) ne fait qu'appeler la fonction, avec un paramètre différent à chaque fois certes, mais sans rien lui retourner...
L'étude de l'exemple suivant, déjà plus "évolué, va nous permettre également de préciser la manière de concevoir un algorithme récursif et tout le vocabulaire qui tourne autour de la récursivité.

Un deuxième exemple un peu plus utile...

On veut maintenant écrire une fonction qui calcule la somme des entiers de 1 jusqu'à N inclus, paramètre passé à la fonction.

Par exemple, pour N = 10, la fonction calculera la somme : 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55

Algorithme itératif

On utilise une boucle dont l'indice varie de 1 jusqu'à N, et on ajoute à chaque tour de boucle la valeur de cet indice à une variable somme :

Algorithme récursif

Cas général

Il faut voir les choses sous un autre angle, et réfléchir cette fois en terme de relation qui existe entre les différentes valeurs additionnées.
On peut ainsi écrire :

• somme(10) = 10 + (9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1)
• or : somme(9) = 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
• Donc : somme(10) = 10 + somme(9)

De même :

• somme(9) = 9 + (8 + 7 + 6 + 5 + 4 + 3 + 2 + 1)
• or : somme(8) = 8 + (7 + 6 + 5 + 4 + 3 + 2 + 1)
• Donc : somme(9) = 9 + somme(8)

Etc, etc...Autrement dit, on a pour un entier N quelconque : somme(N) = N + somme(N - 1). La somme totale est égale à l'entier le plus grand + la somme des entiers inférieurs, elle-même égale à l'entier inférieur + la somme des entiers inférieurs, elle-même égale à etc, etc...

Et voila la relation ( on parle en mathématiques de relation de récurrence ) que nous allons utiliser pour obtenir la somme des N entiers :

def somme_recurs(N):
	
	return N + somme_recurs( N - 1 )
			

→ la fonction va s'appeler elle-même "en chaîne", en se passant à chaque appel un argument différent; le résultat retourné par la fonction sera obtenu à partir de celui retourné par le niveau "inférieur" de récursion, qui lui-même sera obtenu à partir du résultat du niveau encore en dessous, et ainsi de suite...

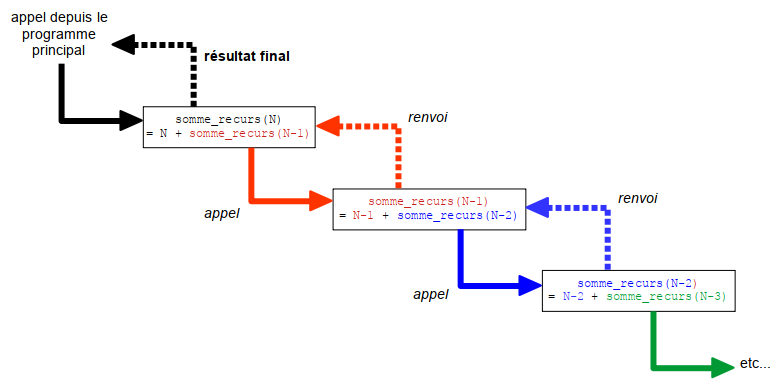
Chaque appel de la fonction n'est donc pas immédiatement suivi du renvoi de son résultat : il est "en attente" du calcul du résultat suivant...Voila pourquoi on parle d'appels récursifs de la fonction = appel réalisé alors que l’interprétation d’un appel précédent de la même fonction n’est pas terminé.

Cas de base

On voit donc qu'il manque encore à notre algorithme une chose indispensable : il faut que les appels successifs de la fonction à elle-même s'arrêtent à un moment, de façon à "déclencher" la "remontée" progressive des résultats d'un niveau de récursion au niveau supérieur, sinon les appels se prolongeront à l'infini sans que l'on n'obtienne aucun résultat !.

Il faut donc prévoir à tout algorithme récursif une condition d'arrêt, que l'on appelle également cas de base. Ce cas correspond à la situation où il n'est pas nécessaire d'effectuer de calcul pour obtenir le résultat qui sera renvoyé au niveau supérieur.

Dans notre exemple, c'est lorsque N = 0 qu'il faut arrêter l'algorithme : en effet, il n'y alors plus rien à calculer.
A ce moment, la fonction doit donc renvoyer 0 ( on n'ajoute plus rien à la somme ) : il n'y a plus de nouvel appel à la fonction, la récursion s'arrête alors, et les différents résultats sont remontés successivement vers les niveaux supérieurs.

La fonction complète :

def somme_recurs(N):
    if N == 0:
        return 0
            
    return N + somme_recurs( N - 1 )
        
print(somme_recurs(10))
			

Tracé des appels successifs

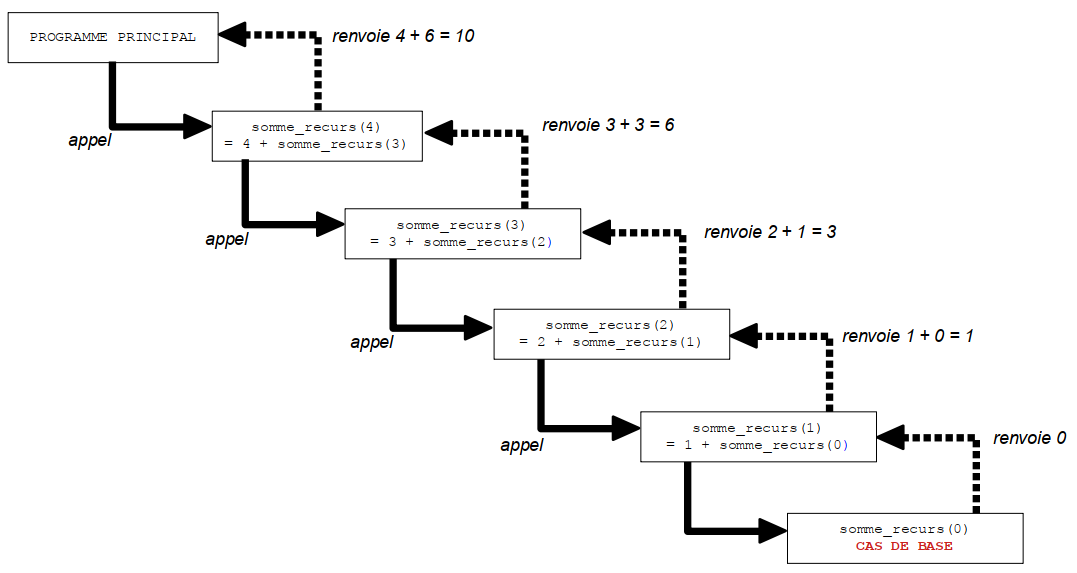
Cela semble peut-être un peu "magique", mais en fait tout est bien entendu parfaitement logique; voila l'arbre des appels et des retours successifs dans le cas où N = 4 ( résultat = 10 ) :

Principes de la récursivité

En résumé, une fonction récursive doit comporter :

Pour illustrer le dernier critère, voila un exemple de récursion qui peut poser problème ( c'est notre tout premier exemple ) :

def f(n):
	# condition d'arrêt
	if n == 0:
		print("Bye-bye !")
	else :
		print("Salut !")
		return f(n-1)
			

Tout est là, cas de base, appel récursif. L'appel de cette fonction avec un paramètre n positif ne pose effectivement aucun problème :

	
	>>> f(5)
			
	Salut !
	Salut !
	Salut !
	Salut !
	Salut !
	Bye-bye !

	>>> 		
			

Par contre, avec n négatif, la condition d'arrêt ne sera jamais vérifiée : la chaîne des appels ne terminera jamais !

	
	>>> f(-5)
	
	Salut !
	Salut !
	.....
	.....
	Salut !
	Salut !
	Salut !
	Salut !
	Traceback (most recent call last):
	  File "test.py", line 8, in 
	    f(-5)
	  File "test.py", line 6, in f
	    f(n-1)
	  File "test.py", line 6, in f
	    f(n-1)
	  File "test.py", line 6, in f
	    f(n-1)
	  [Previous line repeated 1009 more times]
	  File "test.py", line 5, in f
	    print("Salut !")
	RecursionError: maximum recursion depth exceeded while pickling an object
	>>> 
			

( L'erreur alors rencontrée correspond à un "débordement de pile" et est expliquée ci-dessous.)

Sachant que d'après les travaux Alan Turing, il n'existe aucun moyen algorithmique pour prouver qu'un programme se terminera ( voir le chapitre sur la calculabilité ), c'est au concepteur de l'algorithme de vérifier que celui-ci est correctement écrit...

Comparaison itératif / récursif

Que dire ce cette façon d'envisager les algorithmes ? Il se trouve que de nombreux algorithmes itératifs peuvent se transformer en leur version récursive : c'est le cas par exemple des boucles for :

def f(a, n):
	m = 0
	for i in range(n):
		m = m + a 
	return m
						

def f(a, n):
	if n == 0:
		return 0 
	return a + f(a, n-1)
						

( Que fait cette fonction ? Ce sera le but d'un exercice que vous traiterez ci-dessous...mais vous avez peut-être déjà trouvé ?)

Que faut-il mieux utiliser alors ?

D'autres exemples

La fonction mystère

On considère la fonction récursive de l'exemple du paragraphe 3.

SOLUTION

La fonction puissance

On rappelle que la puissance x d'un nombre y est définie par : y^x = y * y * y * ..... * y ( x fois )

Construire une chaîne

Caractère dans une chaîne