Applications concrètes de la récursivité : fractales et coloriage...

La récursivité, ce n'est pas qu'un concept "scolaire" pour se torturer les méninges...voici quelques applications "concrètes" dans lesquelles ce concept est utilisé avec profit.

Dessins de fractales

Les fractales sont des objets géométriques illustrant parfaitement la notion de récursivité : ils sont construits par la "répétition d'eux-mêmes" à des échelles différentes, ce qui fait qu'ils sont identiques à eux-mêmes quelle que soit l'échelle à laquelle on les observe. On trouve des structures fractales dans la nature, comme la coquille de certains coquillages ou l'aspect bien particulier du chou romanesco.

Outil utilisé : la tortue Python

Le module Turtle de Python permet de tracer facilement des dessins en utilisant une "tortue" munie d'un "crayon" lui permettant de laisser une trace derrière elle.
Elle peut avancer, reculer, se placer en un point quelconque du plan, tourner d'un certain angle vers la droite ou la gauche, etc...

Un langage informatique similaire, le logo, a été populaire dans le milieu éducatif dans les années 80.

On importe le module avec l'instruction :


from turtle import *

Parmi les nombreuses instructions disponibles, voici celles qui vous serviront ici :

down() : abaisse le crayon ( la tortue laisse un trace lors de son déplacement )
up() : lève le crayon ( la tortue ne laisse pas de trace en se déplaçant )
forward(i) : avance de i pixels
backward(i) : recule de i pixels
left(a) : tourne vers la gauche d'un angle de a °
right(a) : tourne vers la droite d'un angle de a °
speed(v) : règle la vitesse de la tortue; plus v est petit ( minimum = 0 ), plus le dessin se fait rapidement.
done() : permet de lancer le dessin, ou, sous Pyzo, de pouvoir fermer la fenêtre de dessin une fois celui-ci terminé.

Au démarrage, la tortue est au milieu de la zone de dessin ( coordonnées (0,0) ). Elle est orientée vers la droite, soit d'un angle de 0° par rapport à l'axe des abscisses.

La courbe de Koch

Il s'agit d'une des premières fractales à avoir été décrite.

On la construit ainsi :

on part d'un segment parallèle à l'axe des abscisses.
On divise le segment en 3 parties de même longueur. On construit un triangle équilatéral ayant pour base le segment médian de la première étape, et on en supprime la base.
on recommence à la deuxième étape avec chacun des segments.

La figure est donc obtenu en "traitant" récursivement chacun de ses segments de la manière décrite à l'étape 2 : voila pourquoi, quelle que soit l'échelle à laquelle on regarde cette figure, on voit toujours la même chose...

On obtient théoriquement la figure au bout d'un nombre infini de récursions, mais dans la pratique, on s'arrêtera à une valeur n "raisonnable"...

Première étape de l'algorithme : le motif de base

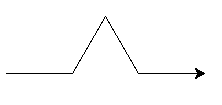
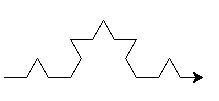
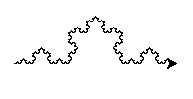
Avant d'utiliser la récursivité, vous allez vous intéresser au tracé d'un premier "motif" correspondant à l'étape 2 de l'algorithme.

Écrire une fonction koch non récursive qui :

prend comme paramètre un nombre entier de pixels c représentant la longueur d'un segment
trace le motif décrit à l'étape 2 de l'algorithme

Vous chercherez le moyen le plus simple pour tracer ce motif à l'aide de la tortue ( il n'est pas nécessaire de suivre à la lettre ce tracé de triangle décrit dans l'algorithme )

from turtle import * def motif_koch(c : int)->None: pass # en FIN de script done()

La courbe de Koch : récursivité !

Il ne vous reste plus qu'à coder la récursivité ( étape 3 de l'algorithme ) : il faut appliquer récursivement votre fonction de tracé du motif sur chacun des segments de ce motif.

En vous inspirant de la logique du code de la fonction précédente ( en la "rendant récursive" ), écrire une fonction courbe_koch récursive qui :

prend comme paramètres un nombre entier de pixels c représentant la longueur du segment et un entier n égal au nombre de récursions souhaité.
construit la courbe de Koch en divisant récursivement chacun des segments

On n'oubliera pas de se poser les questions maintenant habituelles : quel est le cas de base ? Le cas général ?

from turtle import * def courbe_koch(c: int, n : int)->None: pass # en FIN de script done()

SOLUTION

Le triangle de Sierpinski

Il s'agit de la figure montrée en introduction du cours.

On la construit ainsi :

Commencer à partir d'un triangle quelconque du plan, par exemple un triangle équilatéral ayant une base parallèle à l'axe des abscisses.
tracer trois triangles à l'intérieur qui se touchent deux à deux par un sommet, et dont les longueurs des côtés sont la moitié de celles du triangle de départ
recommencer à la deuxième étape avec chacun des petits triangles obtenus.

Fonction auxiliaire de tracé de triangle

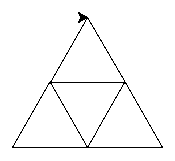
Pour rendre le code plus lisible et pouvoir facilement l'adapter par la suite, vous coderez le tracé d'un triangle dans une fonction à part ( non récursive ).

Écrire une fonction triangle_equi qui :

prend comme paramètre un nombre de pixels c représentant la longueur des côtés d'un triangle équilatéral
trace un triangle équilatéral à partir du point où se trouve la tortue

On prendra soin de faire en sorte de repositionner la tortue dans son orientation d'origine ( 0° ).

from turtle import * def triangle_equi(c : int)->None: pass # en FIN de script done()

Première étape de l'algorithme : le motif de base

Écrire une fonction sierpinski(c) non récursive qui :

prend comme paramètre un nombre entier de pixels c représentant la longueur des côtés d'un triangle équilatéral
trace, en utilisant la fonction triangle_equi() précédente, le motif des trois petits triangles décrit à l'étape 2 de l'algorithme

Là aussi, on fera en sorte que la tortue revienne à son orientation d'origine mais également dans sa position d'origine.

from turtle import * def triangle_equi(c : int)->None: pass def motif_sierpinski(c : int)->None: pass # en FIN de script done()

Le triangle de Sierpinski : récursivité !

Il ne vous reste plus qu'à coder la récursivité ( étape 3 de l'algorithme ).

En vous inspirant de la logique du code de la fonction précédente, écrire une fonction triangle_sierpinski qui :

prend comme paramètres un nombre entier de pixels c représentant la longueur des côtés d'un triangle équilatéral et un entier n égal au nombre de récursions souhaité.
construit le triangle de Sierpinski en divisant récursivement chaque triangle tracé en 3 petits triangles

from turtle import * def triangle_equi(c : int)->None: pass def triangle_sierpinski(c: int, n: int)->None: pass # en FIN de script done()

SOLUTION

D'autres fractales

Voila quelques exemples d'autres fractales que vous pouvez tracer avec la même méthode.

le cas de base est le tracé de l'initiateur de la fractale, c'est à dire "de quoi on part" pour la construire ( un segment pour la courbe de Koch, un triangle pour le triangle de Sierpinski )
le cas général est le tracé récursif du générateur, c'est à dire du "motif" qui permet de construire la fractale en modifiant l'initiateur.

Le flocon de Koch

Le flocon de Koch est obtenu en appliquant l'algorithme de la courbe de Koch à un initiateur de forme géométrique comme un triangle équilatéral ou un carré; c'est donc une courbe de Koch mais en "2D".

Modifier le script du tracé de la courbe de Koch pour qu'il puisse se faire à partir d'un triangle équilatéral ou d'un carré.

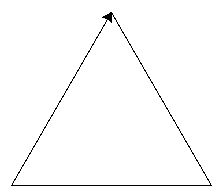
Koch triangle 3 récursions — ...pour arriver à ça ( 3 récursions )

from turtle import * def flocon_koch(c: int, n: int)->None: pass # en FIN de script done()

SOLUTION

Sierpinski bis

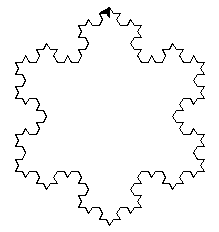
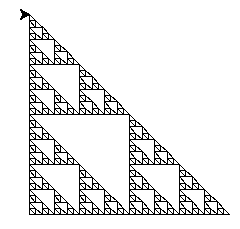
La première étape de l'algorithme de tracé du triangle de Sierpinski n'impose pas de partir d'un triangle équilatéral.

Modifier le code de votre script de tracé du triangle de Sierpinski pour partir d'un initiateur différent comme un triangle rectangle isocèle par exemple. Le reste de l'algorithme ne change pas, notamment la méthode de tracé du générateur est la même.

Il faudra modifier aussi bien la fonction de tracé du triangle que la fonction récursive elle-même.

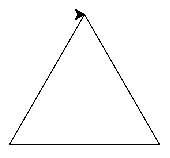
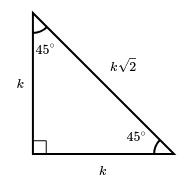
Pour les non-matheux, voila une figure indiquant les longueurs des côtés et les angles dans un triangle rectangle isocèle :

from turtle import * def triangle_equi(c : int)->None: pass def sierpinski_bis(c: int, n: int)->None: pass # en FIN de script done()

SOLUTION

Coloriage automatique

Vous y avez tous joué à ce jeu de coloriage :

Allez, allez, il n'y a pas de honte...

On peut se demander quel algorithme permet le coloriage de zones connexes, c'est à dire les points qui sont tous inclus dans une même zone délimitée ( ici par un trait noir ) et qui devront donc tous prendre la même couleur; c'est l'algorithme derrière l'outil "Pot de peinture" présent dans tous les logiciels de retouche d'images, c'est aussi le même algorithme qui permet de découvrir les zones sans mines au jeu du Démineur, ou, plus étonnant, celui qui permet de trouver la sortie d'un labyrinthe.

Une version assez "élégante" de cet algorithme utilise la récursivité; mais il trouve rapidement ses limites dans le cas de "grandes" quantités de données à traiter, ce qui fait que dans la pratique les usages ci-dessus sont codées d'une autre manière ( que nous aborderons plus tard lors du chapitre sur les parcours de graphes ).

L'algorithme récursif est cependant très simple, et l'utilisation de la récursivité y est intuitive : vous allez donc tout de même vous y intéresser dans cette activité.

Principe

Le point choisi à l'intérieur de la zone à colorier s'appelle le "germe" ou la "graine". A partir de lui, on appelle la fonction de remplissage :

on colorie le point avec la nouvelle couleur
on examine son voisin de gauche : si il n'est pas encore colorié, et n'appartient pas à une "frontière", alors on appelle récursivement la fonction sur ce nouveau point
on fait pareil avec le voisin de droite, celui du haut, et du bas ( et éventuellement, dans une version plus évoluée, le voisin en haut à gauche, en haut à droite, etc...)

Et c'est tout ! Facile, non ? ( en fait, il manque quelques "sécurités" à cet algorithme, notamment vérifier que l'on ne sort pas de la zone de dessin...)


fonction colorier_recursivement(point):
    colorier le point
    si le point à gauche n'est pas encore colorié et n'est pas sur une frontière :
        colorier_recursivement(point à gauche) 
    si le point à droite n'est pas encore colorié et n'est pas sur une frontière :
        colorier_recursivement(point à droite)
    idem pour le point au dessus et le point au dessous...

Mais attendez voir...je vois bien les appels récursifs, mais où est le cas de base ?

Il est en fait "combiné" avec les cas généraux dans l'évaluation des conditions : si le point à colorier est de la couleur d'une ligne frontière ou a déjà été colorié, la récursion s'arrête alors.

Pour savoir si un point peut-être colorié ( c'est à dire qu'il ne l'est pas encore et qu'il n'est pas sur une frontière ), il suffit de tester si il est de la même couleur que celle de la "graine".

Travail sur un exemple simple

Vous n'allez pas tout de suite travailler sur une image : pour bien comprendre le principe, vous allez utiliser un petit tableau de tableaux de 10 x 10 éléments modélisant les pixels d'une image ( si vous avez oublié les notions de pixels, couleurs, etc...relatives aux images, ainsi que l'utilisation des tableaux de tableaux ( = matrices ), vous pouvez revoir le cours de Première à ce sujet ).


p = [[0,0,0,0,0,0,0,0,0,0],
    [0,0,1,1,1,0,0,0,0,0],
    [0,1,0,0,0,1,0,0,0,0],
    [0,1,0,0,0,1,0,0,0,0],
    [0,1,0,0,0,1,0,0,0,0],
    [0,1,0,0,0,0,1,0,0,0],
    [0,0,1,0,0,0,1,0,0,0],
    [0,0,1,0,0,0,1,0,0,0],
    [0,0,0,1,1,1,0,0,0,0],
    [0,0,0,0,0,0,0,0,0,0]]

un "pixel" de valeur 1 représente une "frontière"
un "pixel" à 0 représente un point d'une zone pouvant être "coloriée"

Écrire une fonction récursive remplit_recurs qui :

prend en paramètre le tableau de "pixels" p et les coordonnées x et y d'un "pixel"
mute le tableau de façon à ce que tous les "pixels" de la zone "coloriée" soient remplacés par la valeur 2.


>>> remplit_recurs(p, 3, 4) # germe de coordonnée x = 3 / y = 4 ( 5ème ligne / 4ème colonne )

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 1, 1, 1, 0, 0, 0, 0, 0]
[0, 1, 2, 2, 2, 1, 0, 0, 0, 0]
[0, 1, 2, 2, 2, 1, 0, 0, 0, 0]
[0, 1, 2, 2, 2, 1, 0, 0, 0, 0]
[0, 1, 2, 2, 2, 2, 1, 0, 0, 0]
[0, 0, 1, 2, 2, 2, 1, 0, 0, 0]
[0, 0, 1, 2, 2, 2, 1, 0, 0, 0]
[0, 0, 0, 1, 1, 1, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
>>>

L'ordre dans lequel chaque voisin ( gauche, haut, ...) est traité n'a pas d'importance.

Tenez compte de la remarque faite ci-dessus sur la nécessaire sécurité à apporter à l'algorithme : avant de propager la récursion aux points voisins, il faut d'abord vérifier que l'on ne sortira pas de "l'image". ( On peut sinon rajouter un cadre frontière tout autour de l'image.)

Testez votre fonction avec un germe situé dans chacune des deux zones possibles à "colorier"; vous pouvez aussi éventuellement modifier le tableau de "pixels" pour confirmer le bon fonctionnement de votre fonction.

def remplit_recurs(tab: list[list], x: int, y: int)->None: pass pixels = [[0,0,0,0,0,0,0,0,0,0], [0,0,1,1,1,0,0,0,0,0], [0,1,0,0,0,1,0,0,0,0], [0,1,0,0,0,1,0,0,0,0], [0,1,0,0,0,1,0,0,0,0], [0,1,0,0,0,0,1,0,0,0], [0,0,1,0,0,0,1,0,0,0], [0,0,1,0,0,0,1,0,0,0], [0,0,0,1,1,1,0,0,0,0], [0,0,0,0,0,0,0,0,0,0]]

SOLUTION

Travail sur une image

Vous allez maintenant appliquer votre fonction à une véritable image : une zone blanche à colorier le sera en un niveau de gris donné ( à choisir ! ).

Vous utiliserez l'image ci-dessous :

Téléchargement du fichier

Modifiez votre script précédent pour qu'il traite le tableau de pixels de l'image ci-dessus, de façon à pouvoir colorier une zones de points connexes.

Attention, l'image n'est pas simplement en noir ET blanc, mais contient des niveaux de gris : les frontières ne contiennent donc pas que des pixels noirs; il faudra en tenir compte pour que le script puisse "détecter" ces frontières.

Pour la 'graine', on vous propose des valeurs pour ses coordonnées, mais n'hésitez pas à expérimenter !

Vous allez utiliser le module PIL pour manipuler des fichiers images.

Pour pouvoir utiliser l’utiliser dans l'éditeur ci-dessous, penser à l'installer au préalable.

from PIL import Image def colorie_recurs(t: list[list], x: int, y: int)->None: pass ## Ouverture du fichier, et construction de la matrice des pixels img = Image.open("minion.jpg") pixels = list(img.getdata()) width, height = img.size data = [pixels[i * width:(i + 1) * width] for i in range(height)] ## Remplissage récursif colorie_recurs(data, 50, 100) # coordonnées de la 'graine", valeurs à expérimenter ! ## Construction de l'image img = Image.new("L" ,(len(data[0]), len(data))) data = [pixel for ligne in data for pixel in ligne] img.putdata(data) ## Affichage img.show(img)

SOLUTION

Un programme de coloriage complet

Pour terminer, voila une ébauche d'interface graphique pour utiliser votre algorithme avec la souris, ce qui permettra de sélectionner directement la zone à colorier; il vous suffit d'insérer votre fonction récursive à l'endroit indiqué.

Vous pouvez l'utiliser avec l'image ci-dessous, ou une autre image au format .jpg mais petite ( 100 pixels de côté environ ).

Téléchargement du fichier

( Ah mais dites donc, elles sont bien petites ces images...A votre avis, pourquoi ? )

Vous pourrez faire évoluer cette interface, par exemple en permettant de changer de couleur en cliquant sur le bouton droit de la souris ( évènement '<Button-2>' de Tkinter : RTFM ! )

SOLUTION