TP Diviser pour Régner 1 : rotation d'1/4 de tour d'une image

L'objectif est d'implémenter deux algorithmes permettant de faire tourner une image d'un quart de tour dans le sens des aiguilles d'une montre; en adoptant l'approche "Diviser pour régner", on montrera que la complexité spatiale ( pas temporelle ! ) de l'algorithme est O(1), c'est à dire qu'il se déroule en espace constant ( = sans mémoire supplémentaire autre que celle nécessaire pour stocker l'image d'origine ).

Rappels sur les images

Une image est un tableau bidimensionnel composé de points élémentaires appelés pixels.

Un pixel est, dans le cadre du codage RGB, un triplet d'entiers de valeurs comprises entre 0 et 255 codant respectivement l'intensité lumineuse du rouge (R), du vert (G) et du bleu (B).

Revoir la page de Première pour plus de précision.

Vous utiliserez le module PIL qui permet de gérer des images de format différent, notamment le format JPEG.

On importe ce module en début de script avec l'instruction :


from PIL import Image

Pour ouvrir une image à partir d'un fichier :


img = Image.open("nom_du_fichier.xyz")

La variable img contient alors un objet décrivant les pixels de l'image.

Cet objet propose de nombreuses méthodes, parmi lesquelles les suivantes nous intéressent :

Les dimensions de l'image (en pixels ) peuvent être déterminées par :


largeur, hauteur = img.size

Le tuple codant le pixel de coordonnées (x, y), dans l'image peut être récupéré par :


pixel = img.getpixel((x,y)) # attention, les coordonnées elles-mêmes sont sous forme de tuple

Chaque élément du tuple pixel correspond, dans l'ordre, à la valeur des composantes, R, G et B.

Pour affecter un tuple (r, g, b) à un pixel de coordonnées (x, y) dans l'image, on utilisera :


img.putpixel((x,y), (r, g, b))

Une image peut être sauvegardée avec :


img.save("nom_du_fichier.xyz")

Une image peut être affichée avec l'instruction :


img.show()

Enfin, une image vide ( entièrement noire par défaut ) peut être créée avec l'instruction :


nv_img = Image.new("RGB", (largeur, hauteur))

Pour ce travail, vous utiliserez une image carrée de 512 ⨯ 512 px, que vous pouvez récupérer ici.

Algorithme simple de rotation d'un quart de tour

Avec cet algorithme, on crée une nouvelle image, et on parcourt chacun de ses pixels en leur faisant correspondre un pixel donné de l'image d'origine.

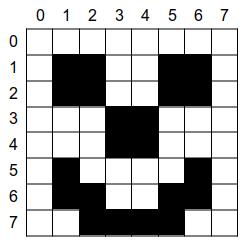
On montre que, pour faire tourner d'un quart de tour une image carrée de n⨯n pixels dans le sens des aiguilles d'une montre, il faut faire correspondre au pixel de coordonnées (y, n - 1 - x) dans l'image d'origine, le pixel de coordonnées (x, y) dans l'image obtenue par rotation.

Écrire une fonction rotation(image) qui prend en paramètre l'objet image d'origine, et qui :

créé une nouvelle image initialement vide, de mêmes dimensions que celle d'origine, destinée à stocker l'image obtenue par rotation de l'image d'origine
stocke dans la nouvelle image les pixels obtenus par la méthode présentée ci-dessus.
renvoie la nouvelle image.

Compléter ensuite le script pour ouvrir un fichier image, faire tourner celle-ci d'1/4 de tour à l'aide de la fonction, et afficher le résultat.

Questions :

Quelle est la complexité temporelle de cet algorithme en fonction de n ( = nombre de pixels horizontaux et verticaux ) ?
Quelle est la complexité spatiale de cet algorithme, c'est à dire l'ordre de grandeur en fonction de n de la taille mémoire utilisée ?

SOLUTION

Algorithme Diviser pour régner

Dans cet algorithme :

l'image est divisée récursivement en 4 "sous-images" de dimensions 2 fois plus petites
une rotation de 1/4 de tour des 4 sous-images est faite; pour réaliser cette rotation, une permutation circulaire des 4 sous-images est faite, qui est réalisée en échangeant dans un certain ordre les sous-images ( voir algorithme ci-dessous )

Il s'agit d'un algorithme récursif : le cas de base est obtenu quand les "sous-images" ne sont plus constituées que d'un unique pixel, et dans ce cas, il est inutile de faire quoi que ce soit.


fonction rotation2(image: image d'origine, x0,y0 : coordonnées du point en haut à gauche de l'image, n : nombre de pixels horizontaux/verticaux):
	
	si n est supérieur ou égal à 2:
		rotation2(sous-image en haut à gauche)
		rotation2(sous-image en bas à gauche)
		rotation2(sous-image en bas à droite)
		rotation2(sous-image en haut à droite)
		
		echanger sous-images(haut à gauche ↔ haut à droite)
		echanger sous-images(haut à gauche ↔ bas à droite)
		echanger sous-images(haut à gauche ↔ bas à gauche)
	fin si

La grande difficulté sera de "délimiter" chaque sous-image : cela se fera en utilisant judicieusement les valeurs de x0, y0 et n ( il va falloir utiliser un papier et un crayon ! )

Déroulement de l'algorithme sur un exemple

Dérouler l'algorithme sur l'exemple de l'image ci-dessous ( à faire au crayon à papier ! ) :

SOLUTION

Fonctions utilitaires

Vous allez tout d'abord coder deux fonctions non récursives qui seront utilisée par l'algorithme précédent :

écrire une fonction echange_pixel() qui échange les pixels de coordonnées (x0, y0) et (x1, y1) d'une image passée en paramètre.


def echange_pixel(image, x0, y0, x1, y1):
	"""
		Fonction qui échange la valeur de deux pixels
		image = image d'origine
		x0, y0 = coordonnées du premier pixel				
		x1, y1 = coordonnées du deuxième pixel		
	"""
	............

écrire une fonction echange_images() utilisant la fonction précédente et qui échange tous les pixels de deux sous-images de taille identique n, et dont les coordonnées du premier point sont passées en paramètre.


def echange_images(image, x0, y0, x1, y1, n):
	"""
		Fonction qui échange les pixels de deux sous-images
		image = image d'origine
		x0, y0 = coordonnées du premier pixel de la première sous-image			
		x1, y1 = coordonnées du premier pixel de la deuxième sous-image
		n = taille des deux sous-images
	"""
	............

SOLUTION

Algorithme de rotation

Écrire maintenant une fonction rotation2(), qui utilise notamment la fonction précédente, et qui traduit l'algorithme présenté.


def rotation2(image, x0, y0, n):
	"""
		Fonction qui échange les pixels de deux sous-images
		image = image d'origine
		x0, y0 = coordonnées du premier pixel de l'image
		n = taille de l'image			
	"""
	............

Dans cette fonction, le paramètre image restera inchangé d'un appel récursif à l'autre; par contre, tous les autres paramètres devront être modifiés car ce sont eux qui vont servir à "délimiter" chacune des sous-images.

Compléter ensuite le script pour ouvrir un fichier image, faire tourner celle-ci d'1/4 de tour à l'aide de la fonction, et afficher le résultat ( attention, la fonction ne renvoie rien : "où" est alors l'image résultant de la rotation ? ).

Question :

On montre ( hors-programme ) que la complexité temporelle de cet algorithme est O(n².log n), moins bonne que celle du précédent, ce qui fait qu'il n'est en réalité pas utilisé dans la pratique du fait de sa lenteur.

Par contre, que peut-on dire de la complexité spatialede cet algorithme ? Pourquoi ?

SOLUTION